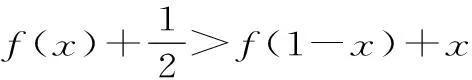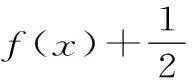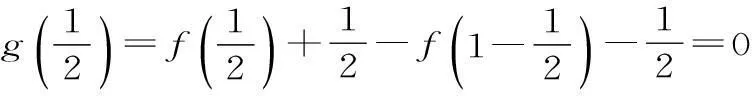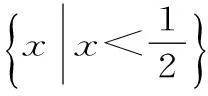一道抽象函数问题的多思路解析



一道抽象函数问题的多思路解析

■丁卓非

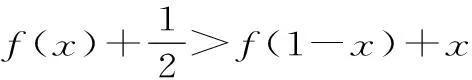
抽象函数是没有给出解析式的函数，在处理此类问题时常常感到无从下手，但因其既能考查函数的概念与性质，又能考查思维能力与抽象能力，是高考中的热点与难点，如何寻找此类问题的突破口是关键。本题短小精悍，但内涵十分丰富，在各类试题中常出现其变形题目，是值得研究的一道好题，所以，借助于有关文献，通过自己的研究，得到本题的三个思路。

下面给出本题的思路分析。

思路一：函数特殊化，探究结果

考虑到是填空题，当填空题的结论唯一或题设条件中提供的信息暗示答案是定值时，可从题中变化的不定量中选取符合条件的恰当特殊值(特殊函数、特殊角、特殊位置、特殊图形、特殊点、特殊方程等)进行处理，从而探求出结论，所以例题可将函数特殊化，找到一个满足条件的具体函数，从而得到结果。

又x<0时，f′(x)=x-1

反思：这种解法的关键是选取恰当的特殊函数，体现双基的重要性。

思路二：从欲解的不等式入手，构造函数，转化、猜想求解

从题中条件知，当x<0时f′(x)0时，f′(x)的关系并未给出，由f(-x)+f(x)=x2知，x与-x是相反数，所以从f(-x)+f(x)=x2求导入手，得到x>0时，f′(x)的关系。

解法2：f(-x)+f(x)=x2,得-f′(-x)+f′(x)=2x，即f′(-x)=f′(x)-2x。

当x<0时，f′(-x)=f′(x)-2x

所以当x>0时，f′(x)

从而得f′(x)

反思：上面的解法说明，解决问题的多种思路、方法与技巧来源于：(1)准确理解与运用数学概念，牢固记忆和灵活运用定理公式等基本知识。

(2)对题目特点及式子结构特征认真分析，对有关知识进行整合，注重观察、联想、转化、猜想等把不熟悉的知识转化为熟悉的已掌握的知识，从而解决问题。

作者单位：河南省驻马店高级中学