空间中的“垂直”关系判定
2016-04-27
空间中的“垂直”关系判定
■张卿
垂直是一种特殊的空间关系,空间中直线与直线垂直、直线与平面垂直、平面与平面垂直三者之间可以相互转化,每一种垂直的判定都是从某种垂直开始转向另一种垂直,最终达到目的,其转化关系可以用图1表示。
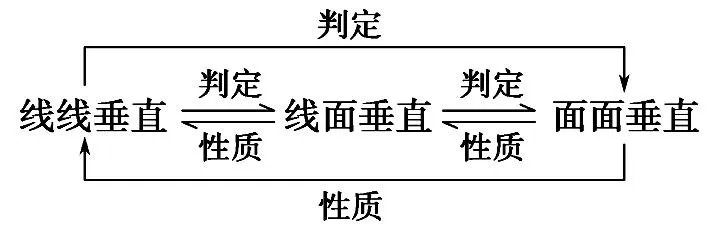
图1
在证明两平面垂直时,一般先从现有的直线中寻找平面的垂线,若这样的直线图中不存在,则可通过作辅助线来解决。
一、直线与平面垂直
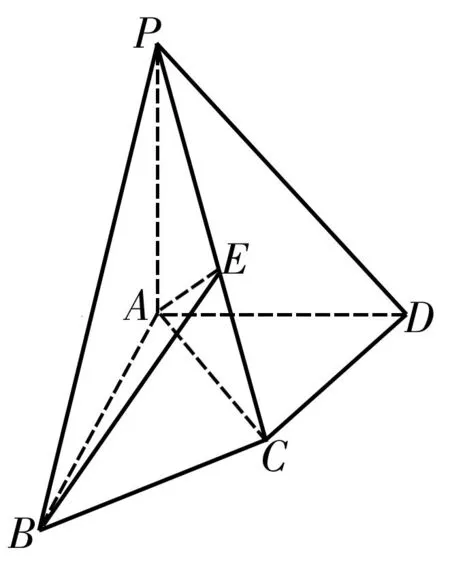
图2
例1如图2,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点。证明:
(1)CD⊥AE;
(2)PD⊥平面ABE。
证明:(1)在四棱锥P-ABCD中,因为PA⊥底面ABCD,CD⊂平面ABCD,所以PA⊥CD。
因为AC⊥CD,且PA∩AC=A,所以CD⊥平面PAC。
而AE⊂平面PAC,所以CD⊥AE。
(2)由PA=AB=BC,∠ABC=60°,可得AC=PA。
因为E是PC的中点,所以AE⊥PC。
由(1)知AE⊥CD,且PC∩CD=C,所以AE⊥平面PCD。
而PD⊂平面PCD,所以AE⊥PD。
因为PA⊥底面ABCD,所以PA⊥AB。
又因为AB⊥AD,且PA∩AD=A,所以AB⊥平面PAD。
而PD⊂平面PAD,所以AB⊥PD。
又因为AB∩AE=A,所以PD⊥平面ABE。
规律方法:(1)证明直线和平面垂直的常用方法:①线面垂直的定义;②判定定理;③垂直于平面的传递性(a∥b,a⊥α⟹b⊥α);④面面平行的性质(a⊥α,α∥β⟹a⊥β);⑤面面垂直的性质。
(2)证明线面垂直的核心是证线线垂直,而证明线线垂直则需借助线面垂直的性质。因此,判定定理与性质定理的合理转化是证明线面垂直的基本思想。
二、平面与平面垂直
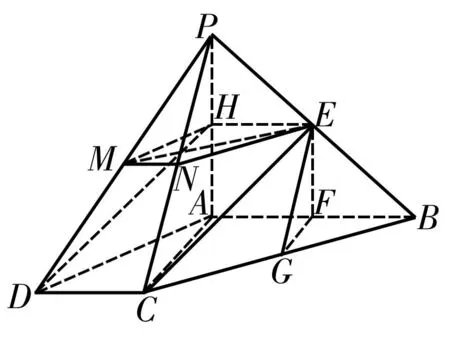
图3
例2如图3,在四棱锥P-ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E、F、G、M、N分别为PB、AB、BC、PD、PC的中点。
(1)CE∥平面PAD;
(2)平面EFG⊥平面EMN。
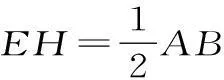
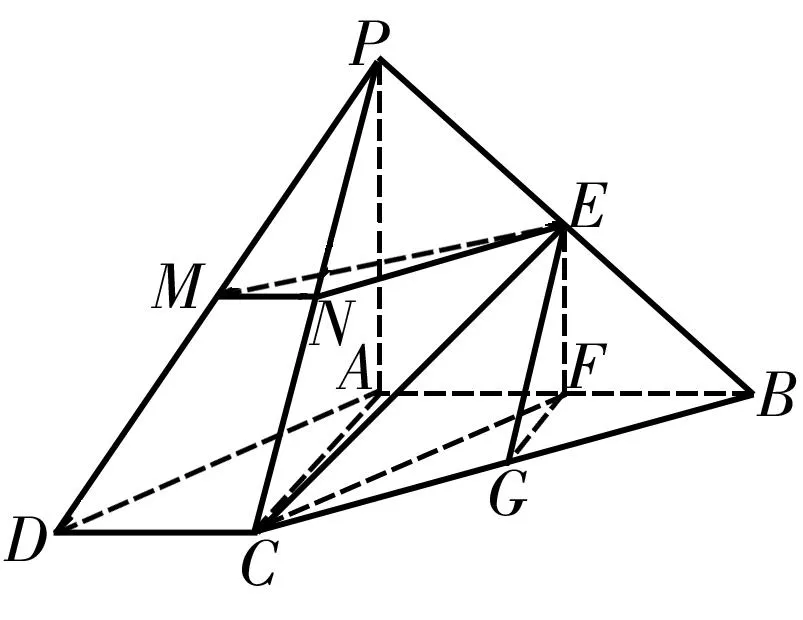
图4
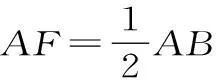
CD。又AF∥CD,所以四边形AFCD为平行四边形。因此CF∥AD。又CF⊄平面PAD,AD⊂平面PAD,所以CF∥平面PAD。因为E、F分别为PB、AB的中点,所以EF∥PA。又EF⊄平面PAD,PA⊂平面PAD,所以EF∥平面PAD。因为CF∩EF=F,故平面CEF∥平面PAD。又CE⊂平面CEF,所以CE∥平面PAD。
(2)因为E、F分别为PB、AB的中点,所以EF∥PA。又AB⊥PA,所以AB⊥EF。同理可证AB⊥FG。又EF∩FG=F,EF⊂平面EFG,FG⊂平面EFG,因此AB⊥平面EFG。又M、N分别为PD、PC的中点,所以MN∥CD。又AB∥CD,所以MN∥AB。因此MN⊥平面EFG。又MN⊂平面EMN,所以平面EFG⊥平面EMN。
规律方法:(1)证明平面和平面垂直的方法:①面面垂直的定义;②面面垂直的判定定理(a⊥β,a⊂α⟹α⊥β)。
(2)已知两平面垂直时,一般要用性质定理进行转化,在一个平面内作交线的垂线,转化为线面垂直,然后进一步转化为线线垂直。
三、易错防范
(1)在用线面垂直的判定定理证明线面垂直时,考生易忽视说明平面内的两条直线相交,而导致被扣分,这一点在证明中要注意。口诀:线不在多,重在相交。
(2)面面垂直的性质定理在立体几何中是一个极为关键的定理,这个定理的主要作用是作一个平面的垂线,在一些垂直关系的证明中,很多情况都要借助这个定理作出平面的垂线。注意定理使用的条件,在推理论证时要把定理所需要的条件列举完整,同时要注意推理论证的层次性,确定先证明什么,后证明什么。
作者单位:江苏省宝应县安宜高级中学
