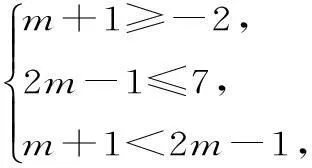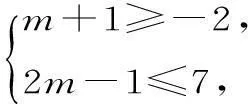《集合及其运算》复习的几点感悟



《集合及其运算》复习的几点感悟

■欧小春

《集合及其运算》是高中数学学习的起点，也是一轮复习的起点，都说好的开始是成功的一半，那么这部分内容如何复习呢？

一、数学思想方法回顾

(1)在解题时经常用到集合元素的互异性，一方面利用集合元素的互异性能顺利找到解题的切入点；另一方面，在解答完毕时，注意检验集合的元素是否满足互异性以确保答案正确。

(2)求集合的子集(真子集)个数问题，需要注意的是：首先，过好转化关，即把图形语言转化为符号语言；其次，当集合的元素个数较少时，常利用枚举法解决，枚举法不失为求集合的子集(真子集)个数的好方法，使用时应做到不重不漏。

(3)对于集合的运算，常借助数轴、Venn图，这是数形结合思想的又一体现。

二、典型例题分析

1.集合的含义。

例1(1)若集合A={x∈R|ax2+ax+1=0}中只有一个元素，则a=()。

A.4B.2C.0D.0或4

解析：(1)由ax2+ax+1=0只有一个实数解，可得当a=0时，方程无实数解；当a≠0时，则Δ=a2-4a=0，解得a=4(a=0不合题意舍去)。

规律方法：(1)用描述法表示集合，首先要搞清楚集合中代表元素的含义，再看元素的限制条件，明白集合的类型，是数集、点集，还是其他类型的集合。

(2)集合元素的三个特性中的互异性对解题的影响较大，特别是含有字母的集合，在求出字母的值后，要注意检验集合中的元素是否满足互异性。

2.集合间的基本关系。

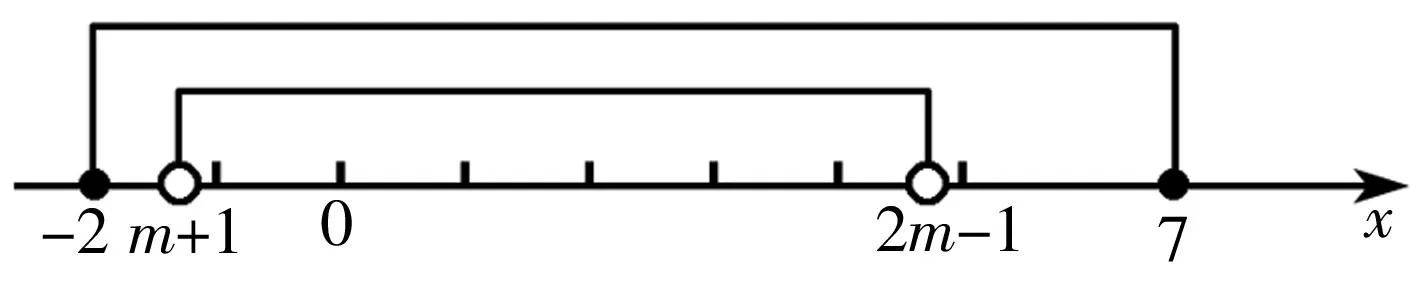
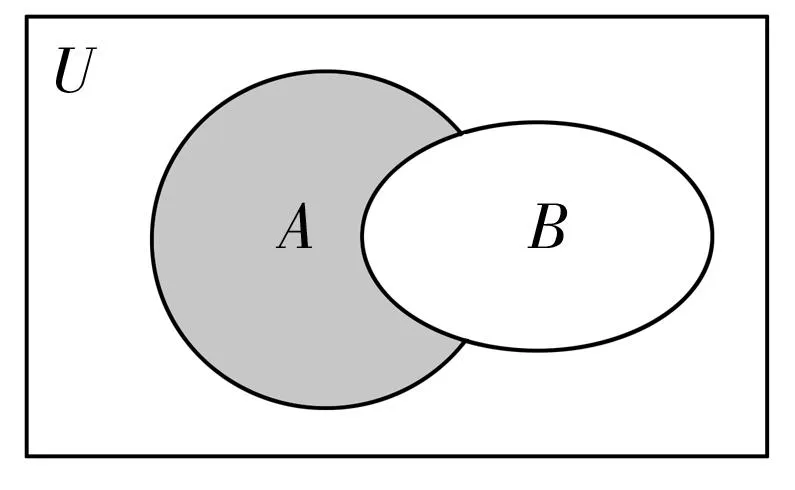
例2(1)已知集合A={x|-2≤x≤7}，B={x|m+1

(2)设U=R，集合A={x|x2+3x+2=0}，B={x|x2+(m+1)x+m=0}，若(UA)∩B=∅，则m=____。

解析:(1)当B=∅时，有m+1≥2m-1，则m≤2。当B≠∅时，若B⊆A，如图1。

图1

解得2

综上，m的取值范围是(-∞，4]。

(2)A={-2，-1}，由(UA)∩B=∅，得B⊆A。

因为方程x2+(m+1)x+m=0的判别式Δ=(m+1)2-4m=(m-1)2≥0，所以B≠∅。所以B={-1}或B={-2}或B={-1，-2}。

①若B={-1}，则m=1；

②若B={-2}，则应有-(m+1)=(-2)+(-2)=-4，且m=(-2)·(-2)=4，这两式不能同时成立，所以B≠{-2}；

③若B={-1，-2}，则应有-(m+1)=(-1)+(-2)=-3，且m=(-1)·(-2)=2，由这两式得m=2。

经检验知m=1和m=2符合条件。所以m=1或2。

规律方法：(1)空集是任何集合的子集，在涉及集合关系时，必须优先考虑空集的情况，否则会造成漏解。

(2)已知两个集合间的关系求参数时，关键是将条件转化为元素或区间端点间的关系，进而转化为参数所满足的关系。常用数轴、Venn图来直观解决这类问题。

3.集合的基本运算。

例3设集合U=R，A={x|2x(x-2)<1}，B={x|y=ln(1-x)}，则图2中阴影部分表示的集合为()。

图2

A.{x|x≥1}

B.{x|1≤x<2}

C.{x|0

D.{x|x≤1}

解析：易知A={x|2x(x-2)<1}={x|x(x-2)<0}={x|00}={x|x<1}，则UB={x|x≥1}，阴影部分表示的集合为A∩(UB)={x|1≤x<2}。

规律方法：(1)一般来讲，集合中的元素若是离散的，则用Venn图表示；集合中的元素若是连续的实数，则用数轴表示，此时要注意端点的情况。

(2)运算过程中要注意集合间的特殊关系的使用，灵活使用这些关系，会使运算简化。

三、易错防范

(1)集合问题解题中要认清集合中元素的属性(是数集、点集，还是其他类型的集合)，要对集合进行化简。

(3)Venn图图示法和数轴图示法是进行集合交、并、补运算的常用方法，其中运用数轴图示法要特别注意端点是实心还是空心。

作者单位：湖南省衡阳市第一中学