解决《平面向量的数量积》的方法例析



解决《平面向量的数量积》的方法例析

■刘诗桂

一、知识梳理

1．平面向量的数量积。

(1)定义：已知两个非零向量a与b，它们的夹角为θ，则数量|a||b|cosθ叫做a与b的数量积(或内积)，记作a·b，即a·b=|a||b|cosθ，规定零向量与任一向量的数量积为0，即0·a=0。

(2)几何意义：数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosθ的乘积。

2．平面向量数量积的运算律。

(1)a·b=b·a(交换律)。

(2)λa·b=λ(a·b)=a·(λb)(结合律)。

(3)(a+b)·c=a·c+b·c(分配律)。

3．计算数量积的三种方法。

定义、坐标运算、数量积的几何意义，要灵活选用，与图形有关的不要忽略数量积几何意义的应用。

二、例题解析与方法归纳

1.例题呈现。

深度思考：对于例2同学们首先想到的方法是什么？这里提醒同学们此题可有三种解法：法一，利用定义；法二，利用向量的坐标运算；法三，利用数量积的几何意义，你不妨试一试。

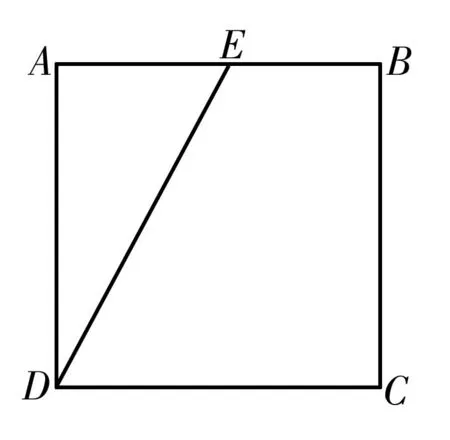
图1

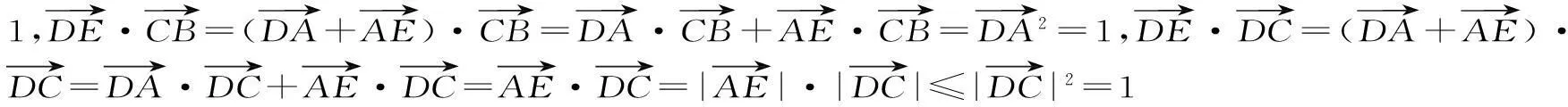
图2

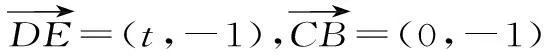
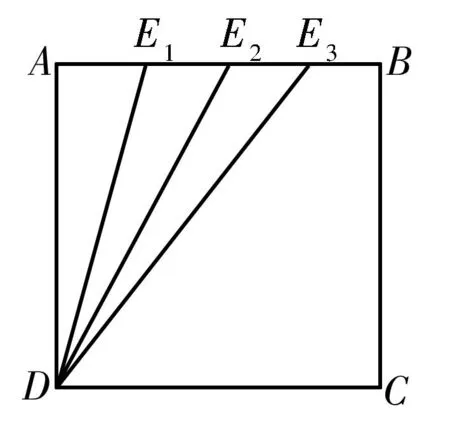
图3

2．规律方法归纳。

求两个向量的数量积有三种方法：利用定义；利用向量的坐标运算；利用数量积的几何意义。

解决涉及几何图形的向量数量积运算问题时，可先利用向量的加减运算或数量积的运算律化简后再运算。但一定要注意向量的夹角与已知平面角的关系是相等还是互补。

作者单位：湖南省衡东县第一中学