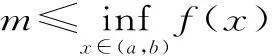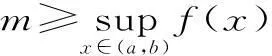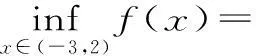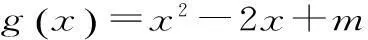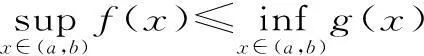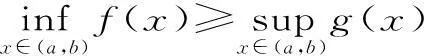浅谈恒成立思想的推广



浅谈恒成立思想的推广

■易如跃孙涛

恒成立问题是近年来高考的一大考点，每年高考各省市的试卷中都有其身影。本文将对如下恒成立论断进行叙述和论证。

其一，已知函数f(x)，x∈[a,b]，若m

其二，已知函数f(x)，x∈[a,b]，若m>f(x)恒成立，则m>fmax(x)。

但此时问题就出现了，对于连续函数f(x)，它在闭区间[a,b]上一定有最值，但在开区间(a,b)上就不一定有最值。若再用恒成立思想解题将遇到尴尬境界。为了解决此类问题，我们想到了数学分析中的确界原理。利用确界就可以解决最值不存在的问题。

定义：设f(x)为定义在区间(a,b)上的函数，若存在实数M(L)使得对一切x∈(a,b)都有f(x)≤M或f(x)≥L，则称f(x)为(a,b)上有上(下)界的函数。M(L)称为f(x)在(a,b)上的一个上(下)界。

对于函数f(x)在任何有限区间上都有界，根据确界原理可知，f(x)在区间(a,b)有上(下)确界。而所谓上确界即最小的上界，下确界即最大的下界。同时，若f(x)有最值，则最大值必为上确界，最小值必为下确界。

(1)恒成立思想的推广。

例题设函数f(x)=-x2+2x，x∈(-3,2)，若m

点评：通过此种方法，进一步验证了恒成立思想的推广对解决函数最值不存在的情况有较强的应用价值，同时也为问题的解决提供了理论支持。

方法二：由题可知，m<-x2+2x，即x2-2x+m<0在(-3,2)上恒成立。

点评：本方法是对二次函数图像性质的进一步应用，旨在培养学生的数形结合思想。

(2)恒成立思想的进一步推广。

方法三：由题可知，m<-x2+2x，即2x-m>x2在(-3,2)上恒成立。

令g(x)=2x-m,h(x)=x2，显然g(x)在(-3,2)上无最小值，h(x)在(-3,2)上无最大值。

点评：在函数无最值的情况下，恒成立思想的进一步推广，给我们解决恒成立问题提供了思想方法。

本文通过对恒成立问题的进一步研究，将高等数学中的确界引入到问题的解决中来，通过实例验证，发现此种思想为解决恒成立问题提供了理论支持。同时也为广大考生解决此类问题提供了方法和思路。

作者单位：安徽省合肥新城高升学校