“离散型随机变量及其分布列”一轮复习例析



“离散型随机变量及其分布列”一轮复习例析

■赵长青

“离散型随机变量及其分布列”这部分内容涉及如下三个考点，每个考点笔者都配上了具体的例题进行分析。

一、离散型随机变量分布列的性质

例1设X是一个离散型随机变量，其分布列为：

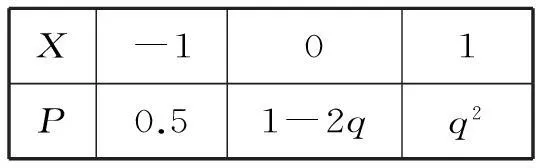
X-101P0.51-2qq2

则q等于()。

解析：由分布列的性质，得：

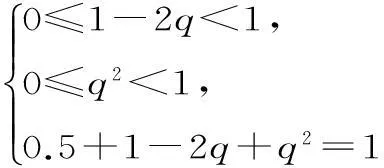
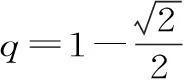
规律方法：(1)利用分布列中各概率之和为1可求参数的值，此时要注意检验，以保证每个概率值均为非负数。

(2)求随机变量在某个范围内的概率时，根据分布列，将所求范围内各随机变量对应的概率相加即可，其依据是互斥事件的概率加法公式。

二、求离散型随机变量的分布列

例2在一个盒子中，放有标号分别为1，2，3的三张卡片，现从这个盒子中，有放回地先后抽得两张卡片的标号分别为x，y，记X=|x-2|+|y-x|。

(1)求随机变量X的最大值，并求事件“X取得最大值”的概率；

(2)求随机变量X的分布列。

解析：(1)由题意知，x、y可能的取值为1、2、3。则|x-2|≤1，|y-x|≤2。

所以X≤3，且当x=1，y=3或x=3，y=1时，X=3。

因此，随机变量X的最大值为3。

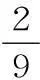
(2)X的所有取值为0、1、2、3。

则随机变量X的分布列为：

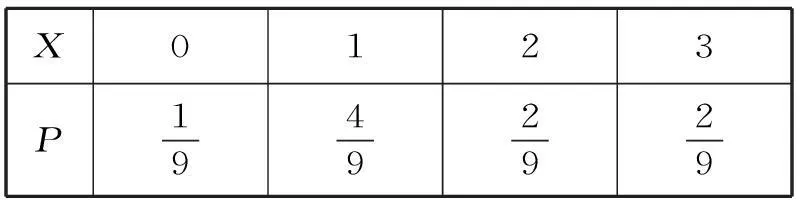
X0123P19492929

规律方法：(1)求解离散型随机变量X的分布列的步骤：第一，理解X的意义，写出X可能取的全部值；第二，求X取每个值的概率；第三，写出X的分布列。(2)求离散型随机变量的分布列的关键是求随机变量所取值对应的概率，在求解时，要注意应用计数原理、古典概型等知识。

三、超几何分布

例3PM2.5是指悬浮在空气中的直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物。根据现行国家标准GB3095-2012，PM2.5日均值在35微克/立方米以下空气质量为一级；在35微克/立方米～75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标。

从某自然保护区2015年全年每天的PM2.5监测数据中随机地抽取10天的数据作为样本，监测值频数如下表所示：

PM2.5日均值(微克/立方米)[25,35](35,45](45,55](55,65](65,75](75,85]频数311113

(1)从这10天的PM2.5日均值监测数据中，随机抽出3天，求恰有一天空气质量达到一级的概率；

(2)从这10天的数据中任取3天数据，记X表示抽到PM2.5监测数据超标的天数，求X的分布列。

解析：(1)记“从10天的PM2.5日均值监测数据中，随机抽出3天，恰有一天空气质量达到一级”为事件A，则：

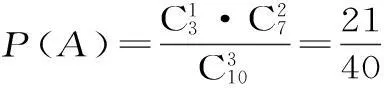
(2)依据条件，X服从超几何分布，其中N=10，M=3，n=3，且随机变量X的可能取值为0，1，2，3。

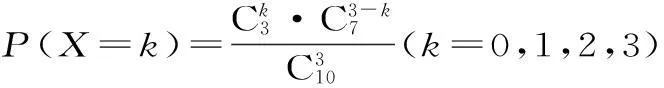
所以随机变量X的分布列为：

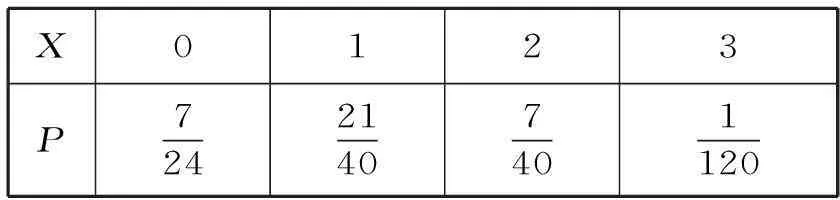
X0123P72421407401120

规律方法：对于服从某些特殊分布的随机变量，其分布列可以直接应用公式给出。超几何分布描述的是不放回抽样问题，随机变量为抽到的某类个体的个数，超几何分布是一个重要分布，其理论基础是古典概型，主要应用于抽查产品，摸不同类别的小球等概率模型。

作者单位：山东省即墨市第二职业中等专业学校