拓展迁移 事半功倍——谈一道课本例题的变式



拓展迁移事半功倍
——谈一道课本例题的变式

■丁华干

朱熹在《观书有感》写道：“问渠哪得清如许,为有源头活水来！”人民教育出版社蔡上鹤先生，在《重视数学经典的传播》一文中也曾指出，中学数学教科书是教材编者根据数学课程标准或者大纲编写的，也是高考命题、组卷的主要参照之一。数学教科书里包含大量典型问题及其适度的延伸。在应用时，要留时间让学生用典、说典、评典、拓典。[1]

为了加深对数学概念的理解与应用，往往需要借助一些典型例题的变式拓展，分析求解，让学生对概念的掌握和理解转化为解决实际问题的技能，形成知识迁移，从而获得事半功倍的学习效果。

下面，本文结合苏教版必修4第三章第3节“两角和与差的正切”的例题4，谈一点初浅的思考，借以抛砖引玉。

例题在斜三角形ABC中，求证：tanA+tanB+tanC=tanAtanBtanC。

分析：这是一个轮换对称的优美的三角恒等式，将所求证的等式与两角和(差)的正切公式比较，都含有正切的和与积，因此，我们可考虑运用两角和的正切公式。

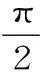
反思与探究：从上述的证明过程我们可以看到，等式成立的关健是A+B+C=π，当然，还必须保证tanA、tanB、tanC都有意义。那么，一般地，当角A、B、C满足什么条件时，能使等式tanA+tanB+tanC=tanA·tanBtanC成立？通过观察，同学们很容易回答一个特殊情况，即A=B=C=0时等式成立。

结论：tanA+tanB+tanC=tanA·tanBtanC成立的充要条件A+B+C=nπ(n∈Z)。

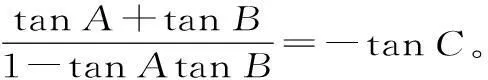
变式拓展1：在斜三角形ABC中，求证：

(1)tan(nA)+tan(nB)+tan(nC)=tan(nA)tan(nB)tan(nC)。

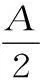
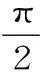
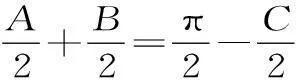
变式拓展2：在△ABC中，tanA+tanB+tanC>0是△ABC为锐角三角形的()。

A．既不充分也不必要条件

B．充分必要条件

C．必要不充分条件

D．充分不必要条件

分析：首先证明充分性。

由例题的证明可知：在△ABC中，tanA+tanB+tanC=tanAtanBtanC。

①若△ABC中有一个钝角，tanA、tanB、tanC必有一个值为负值。即tanAtanBtanC<0，不合条件。

②若三角形有一个为直角，则tanA·tanBtanC无意义。所以当tanA+tanB+tanC>0时,三个角为锐角，故tanA+tanB+tanC>0时，△ABC是锐角三角形。

再证明必要性。因为△ABC是锐角三角形，所以tanA>0,tanB>0，tanC>0。又在△ABC中，tanA+tanB+tanC>0，故正确答案选：B。

变式拓展3：在锐角△ABC中,求证tanAtanBtanC>1。

方法1：由例题的证明可知,在△ABC中，tanA+tanB+tanC=tanAtanBtanC。要证明tanAtanBtanC>1，只要证明tanA+tanB+tanC>1即可。

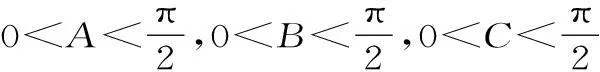
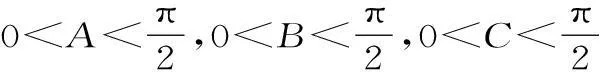
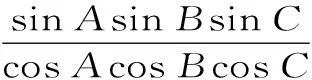
总之，对课本中的例题如果能够做到合理变式拓展与研究设计，让不同基础，不同能力层次的学生，获得数学情感的积极体验，一定会让学生的数学思维能力得到深层次的训练，同时，还能够促进学生自主知识与方法体系的有效建构。这种举一反三的探究过程，也必然会更加激发学生的数学学习兴趣，使我们的数学学习收到事半功倍的效果。

参考文献：

1.蔡上鹤.重视数学经典的传播[J].中学数学教学参考(上),2008(12).

作者单位：江苏省东台市安丰中学