双时滞影响下的桥梁减震半主动控制系统研究

曹雪琴 胡思苗 马 婧

（重庆交通大学 土木工程学院 重庆 400074）

双时滞影响下的桥梁减震半主动控制系统研究

曹雪琴 胡思苗 马 婧

（重庆交通大学 土木工程学院 重庆 400074）

迄今为止，桥梁减震装置的发展已较为成熟，但在考虑时间滞后的复杂性上还存在一定局限。本文对连续梁桥和减震系统进行建模分析，利用线性增益矩阵构建出带有双时滞的桥梁结构运动控制方程；探讨桥梁减震半主动控制系统的局部稳定性；并以某座大跨连续梁桥为工程实例，进行半主动控制地震反应的数值仿真分析。结果表明，在一定条件下，双时滞补偿可以取得较好的减震控制效果。

桥梁减震；半主动控制；时滞动力系统；局部稳定性；增益矩阵

0 引言

近年来诸多关乎桥梁稳定的问题也开始涌现出来。桥梁所处的外部环境不断变化，当其无法适应外部环境的动荷载作用（如地震及风震作用）时，我们需要将桥梁结构设计成为一种能够抵抗外部动力荷载的被动型结构。同时由于减震系统在工作时不可避免的会在信号传输、计算、执行等过程中消耗一定的时间，因此时滞对于减震中的影响不容忽视。本文主要针对带有双时滞因素的桥梁减震半主动控制系统进行研究。

1 控制方法概述

1.1 主动控制

结构主动控制是利用外部能量，在结构受激励振动过程中，对其施加控制力或改变动力特性，从而有效地减小结构的振动。目的是使主动控制系统在满足相应的状态方程和各种约束条件下，选择合适的增益矩阵与最优的控制参数，使系统的性能指标达到较优的状态。

1.2 半主动控制

半主动控制属于参数控制，其控制过程依赖于结构反应及外部激励信息，通过少量能量而实时改变结构的刚度或阻尼等参数，达到降低结构振动的目的。与主动控制相比，半主动控制不需要大量外部能量的输入，只用少量的能量调节就能够主动地利用结构振动往复相对变形或速度，从而实现半主动最优控制。

2 半主动控制计算

2.1 连续梁桥有限元模型

本研究对象是一座全长350m的3跨预应力混凝土连续梁桥，墩高68m，跨径布置为:78m+136m+78m。主梁截面形式为单箱单室截面，支座采用盆式橡胶支座。

图1 连续梁桥有限元模型

2.2 连续梁桥力学模型

本文以连续梁桥为基本研究对象，图 2表示的是在总体坐标系下，具有n个自由度的纵向振动连续梁模型，它用来模拟连续梁的动力行为。

规定：m为质量，k为刚度，c为阻尼参数，ρ为密度，A为横截面面积，l为自由端长度，E为弹性模量，P为比例反馈增益矩阵。

以上述梁为基准，在荷载F作用下（其中F为外部因素），连续梁产生的总位移为f，两者之间的关系式为：

图2 带有时滞τ且具有n个自由度的连续梁桥模型

同理，在n个自由度的力学模型中有：

故刚度k可表示为：

此处我们只考虑单自由度的情况，即n=1，尽量使参数m与此离散模型的固有频率值相匹配。

减震器中的阻尼c则被视为内部因素，其值与成比例变化：

I为n×n阶矩阵。

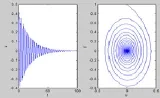
图3 时滞关系图（τ1=1.2s）

图4 时滞关系图（τ1=1.3s ）

图5 时滞关系图（τ1=1.4s

图6 时滞关系图（τ1=1.315s）

2.3 单自由度桥梁模型稳定性分析

前文详细介绍了单自由度的稳定性域的推导过程。由于稳定性域构建于系统的控制参数平面，而桥梁减震装置中的机械和几何参数则被认为是固定的，故得到常比例增益矩阵P和时滞τ。

对于单自由度的情况，方程（7）可简化为：

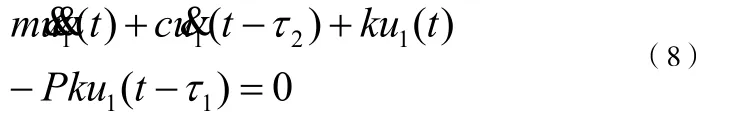
这种方法可以用来计算二维曲线的稳定性边界，从而得知双时滞调和振荡器经历了Hopf分岔。更确切地说，特征值是穿过虚轴的。所以当λ=iω时，特征方程被分为实数部分和虚数部分，故有：

由于特征方程是滞函数，故特征方程的根也是时滞函数。众所周知，当系统有零特征值或者一个纯虚根时，稳定性会变化。当时滞长度变化时，常数解的稳定性也可能变化。

以上方程可以用来求解常比例增益矩阵P和时滞τ，具体求解方法如下：

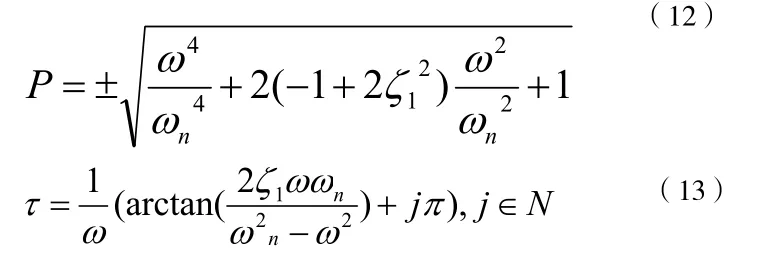
为了确定特征值在关键点的运动情况，需要根据参数求得特征方程D()λ的偏导数。因为特征值的虚数部分对其稳定性无影响，所以只有实数部分才是有意义的。因此，通过隐函数可计算得到：

表1列出了一部分二维曲线的偏导数值。其中所有的上下标注都是有意义的，且所有的分母都为正。

表1 偏导数和的实数部分

表1 偏导数和的实数部分

偏导数PD∂∂Re ∂τ∂DRe 0 2 4 2 4τω τ ωnnPP0 1 2 4 4 2 3 4τ+4πτnnPωPω2 4 4 2 2 2 2Pωτ+4ππnnPω2 4 4 2 2 2-8Pτ π ω+ 16πnnPωΛ 2 2 4 4 2 3 4τ+16πτnnPω PωΛ Λ n 2 4 4 2 3 4τ+2πτn)PωPωnn（2 4 4 2 2 2 2 1 (-τ+2ππωn)Pω2nPnnn-）（1

图7 不动点的局部稳定性域（ζ1=0）

上图表示为增益矩阵P和延迟时间τ的函数关系，近似曲线即稳定性域的边界。在此边界上，半主动控制系统的运动轨迹呈周期性变化，即临界稳定状态；在近似曲线之内的区域，系统的运动轨迹趋于不动点；在近似曲线之外的部分，系统的运动轨迹发散，处于不稳定状态。

3 研究结果

计算结果表明，在一定条件下，双时滞补偿可以取得较好的减震控制效果。时间滞后对桥梁半主动控制的影响非常显著,且时滞使得半主动控制系统对地震反应的减震效果降低，减震效果随着时滞常数的增大而变差。

4 结论

(1)通过对理想控制系统的线性反馈增益矩阵进行简单的修改，实现了一种解决时滞效应的反馈补偿方案。

(2)在模拟过程中，假设结构性能不随时间而改变，但在严重地震时的元素经常处于在弹塑性或塑性阶段，在这种情况下，当前的控制算法是不足的，与其同步进行的工作是：在开发过程中，将考虑了线性增益矩阵的变化视为一种模型结构性质变化的已知功能。

[1]Mohamed Abdel-Rohman,and A.H.Nayfeh,Active Control of Nonlinear Oscillations in Bridges,ASCEJournalofEngineering Mechanics,1987,Vol.113 N°3,p.335-348.

[2]丁皓江，何福保，谢贻权,等.弹性和塑性力学中的有限单元法[J].北京:机械工业出版社,1989:1-215.

[3]亓兴军，李小军，周国良.行波效应对大跨刚构连续桥梁半主动控制影响分析[J]，地震学报，2006,28(2):190-196.

U45

B

1007-6344（2016）10-0024-02