基于四元数指数矩的鲁棒彩色图像水印算法

王向阳　杨红颖　牛盼盼　王春鹏

(辽宁师范大学计算机与信息技术学院　辽宁大连　116081)

(wxy37@126.com)



基于四元数指数矩的鲁棒彩色图像水印算法

王向阳杨红颖牛盼盼王春鹏

(辽宁师范大学计算机与信息技术学院辽宁大连116081)

(wxy37@126.com)

Quaternion Exponent Moments Based Robust Color Image Watermarking

Wang Xiangyang, Yang Hongying, Niu Panpan, and Wang Chunpeng

(SchoolofComputerandInformationTechnology,LiaoningNormalUniversity,Dalian,Liaoning116081)

AbstractIt is a challenging work to design a robust color image watermarking scheme against geometric distortions. Moments and moment invariants have become a powerful tool in robust image watermarking owing to their image description capability and geometric invariance property. However, the existing moment-based watermarking schemes were mainly designed for gray images but not for color images, and detection quality and robustness will be lowered when watermark is directly embedded into the luminance component or three color channels of color images. Furthermore, the imperceptibility of the embedded watermark is not well guaranteed. Based on algebra of quaternions and exponent moments theory, a new color image watermarking algorithm robust to geometric distortions is proposed in this paper. We firstly introduce the quaternion exponent moments to deal with the color images in a holistic manner, and it is shown that the quaternion exponent moments can be obtained from the conventional exponent moments of each channel. Then we provide a theoretical framework to construct a set of combined invariants with respect to geometric distortions (rotation, scaling, and translation). And finally, we present a new color image watermarking algorithm robust to geometric distortions, which is based on a set of quaternion exponent moments invariants. Experimental results show that the proposed color image watermarking is not only invisible and robust against common signals processing such as median filter, noise adding, and JPEG compression, but also robust against the geometric distortions.

Key wordscolor image watermarking; geometric distortions; algebra of quaternions; exponent moments; quantization

摘要近年来，抗几何攻击数字图像水印方法研究取得了很大进展，但现有绝大多数图像水印嵌入算法都是针对灰度图像的，直接用于彩色载体图像的数字水印算法较少.即使原始载体是彩色图像，大部分方法也只是通过提取其亮度信息或使用单色通道信息嵌入数字水印.也就说，现有算法未能很好体现和保留不同色彩分量在整个颜色空间内的特定联系，因而必然影响数字水印的鲁棒性和不可感知性.以四元数与指数矩理论为基础，提出了一种基于四元数指数矩的抗几何攻击彩色图像水印算法.1)把传统灰度图像的指数矩理论推广到四元数层面，并定义出彩色图像的四元数指数矩；2)对四元数指数矩的不变特性进行推导与分析；3)构造出基于四元数指数矩的抗几何攻击彩色图像水印方案.仿真实验表明，该算法不仅具有较好的不可感知性，而且对常规信号处理和几何攻击均具有较好的鲁棒性.

关键词彩色图像水印；几何攻击；四元数；指数矩；量化

抗几何攻击的强鲁棒数字图像水印方法研究是一项富有挑战性的工作[1].一般说来，对于给定的数字图像水印算法，水印检测器必需知道数字水印嵌入的确切位置.所谓几何攻击，并非指该种攻击能够从含水印对象中去除水印信息，而是指其能够破坏数字水印分量的同步(即改变水印嵌入位置)，从而导致检测器找不到有效水印.几何攻击包括旋转、缩放、平移、长宽比改变等多种形式.截止到目前，人们主要采用5种措施设计抗几何攻击的鲁棒图像水印方案，分别为穷举搜索、扩频水印扩频码相结合、同步校正、利用原始数据重要特征、构造同步不变量等[2-3].其中，穷举搜索是图像信号在遭受时域几何攻击后恢复数字水印的最简单方法.通过定义有关参数(如图像旋转、缩放)的变化范围及变化步长，使它们的每种组合代表一个假设已经对作品进行的攻击.检测水印时首先逆转每个可能的组合，然后各应用一次水印检测器.显然，穷举搜索方法存在2点致命不足：1)计算代价太高，其计算量将随着搜索空间的增大而急剧膨胀；2)对水印检测器多次操作会增加虚警率.可见，只有在小搜索空间时，穷举搜索方法才有效，即该方法不利于实际应用[2-3].

从通信角度来看，原始载体图像可以被认为是近似连续幅度的、二维的、有限带宽的并具有较大平均噪声功率的信道，欲嵌入的数字水印是信息或信号，而对含水印图像的攻击可以被看作是在信道中引入的失真或畸变.显然，数字图像水印技术非常接近于典型通信理论，因此许多在连续信道上进行调制通信的方案，都可以作为数字水印技术的潜在方案，这为扩频技术在数字水印领域的广泛应用奠定了基础.一般说来，基于扩频原理的图像水印嵌入方案，往往首先采用误差纠错编码技术，对数字水印信息进行预编码，然后利用相移键控(PSK)等调制方法，对水印信息进行频谱扩展，最后将扩频水印信息直接加入到原始图像的像素值(或变换系数)中.而常见的数字水印检测方案包括2种：

1) 计算扩频序列与含水印图像的互相关性，再通过阈值判定得出数字水印信息；

2) 对含水印图像进行复原滤波，求得复原图像与含水印图像的差值，再与扩频序列进行相关检测.

扩频水印扩频码相结合方法的优点是无需额外同步信息，但由于其缺乏必要的同步保护机制，故普遍无法抵御长宽比改变等较复杂几何攻击.此外，现有部分扩频水印扩频码相结合方案无法实现水印信息的盲检测，因而不利于实际应用[4-5].

所谓同步校正方法是指首先利用相关技术计算出受攻击含水印图像所经历的各种变换参数(如旋转角度、缩放倍数等)，然后对受攻击含水印图像进行同步校正(即进行逆变换)，最后从校正后含水印图像中提取数字水印.显然，各种变换参数的正确计算是该类图像水印方法的关键.基于同步校正的鲁棒图像水印方案主要包括图像配准方法、模版或可识别结构嵌入方法、SVM同步校正方法等.基于配准的数字图像水印方法能够较好抵抗几何攻击，但其提取水印时需要原始载体图像参与，故不利于实际应用.基于模版或可识别结构的图像水印技术具有2个缺点：

1) 模版或可识别结构的嵌入会占用本可用于嵌入水印信息的空间，因而会影响水印的容量;

2) 容易受到模板移除攻击，因为在算法己知的情况下任何人都可以对模扳进行操作，将其去除.

而基于SVM同步校正的图像水印方案具有时间复杂度较高等弱点[6-7].利用原始数据重要特征的图像水印，即所谓“第2代数字图像水印”，其基本思想为：利用相对稳定的图像特征点来标识水印嵌入位置，并在与每个特征点相对应的局部特征区域内独立地嵌入水印信息，同时利用特征点来定位和检测数字水印，从而有效抵抗几何攻击.然而目前该类方法普遍存在特征点稳定性差且分布极不均匀、水印容量十分有限、时间复杂度较高等问题[8-10].

相比较而言，基于同步不变量的图像水印方案以其工作原理简单、无需辅助信息、检测性能稳定等特点而日益受到人们重视[11-19].这类算法的基本思想是从原始图像中找到具有同步不变性的量用来隐藏水印，而目前人们所采纳的同步不变量主要包括Fourier-Mellin变换、Radon变换、几何不变矩、直方图和奇异值等.由于具有同步不变性，在水印图像遭受攻击后，这些量没有变化，因而隐藏于其中的水印信息得以保存.大多数图像水印算法在对含水印载体进行几何攻击后，提取水印时存在许多问题.为克服这个弱点，研究者陆续提出了基于Fourier-Mellin变换的数字水印嵌入算法[11]，该类算法首先计算图像DFT，并对DFT的幅值进行LPM(log-polar map, LPM)，即将笛卡儿坐标系变为对数极坐标系；再对对数极坐标上的系数做DFT，并只取DFT的幅值，从而得到具有仿射变换不变性的空间；最后将水印信息嵌入到仿射变换不变空间内.为抵抗几何攻击，文献[12]引入2种广义Radon变换，提出了一系列鲁棒性能较好的图像水印方案.该类图像水印嵌入方案的核心思想如下：1)利用拐角检测算法检测图像内容中的拐角并找到其中鲁棒性最强的，该拐角被用作2个一维广义Radon变换的原点;2)水印嵌入和检测过程从2个变换中抽取出特征值，并在嵌入或相关检测之前对参考水印进行仿射变换校正.于是，水印嵌入与水印相关检测的同步得以实现.结合计算机视觉和模式识别领域广泛使用的归一化矩概念，文献[13]等文献相继提出了基于Zernike、伪Zernike、Krawtchouk、Tchebichef等不变矩的鲁棒图像水印嵌入技术.此外，Coatrieux等人[14]结合直方图形状不变特性，相继提出了基于像素(或变换系数)统计特征的空间域(或变换域)图像水印方法.Bhatnagar等人[15-16]以小波框架变换、可逆随机扩展变换及奇异值分解(SVD)理论为基础，提出了一种新的数字图像水印方法，该方法可以通过奇异值调制修改等措施，同时在原始载体内嵌入2个数字水印.为了取得不可感知性和鲁棒性的良好平衡.Niu等人[17]结合不变质心理论，提出了基于彩色图像归一化的非下采样轮廓变换(NSCT)域数字水印算法，获得了一定的抗全局几何攻击能力.

以上分析表明，抗几何攻击数字图像水印方法研究已取得了很大进展，但现有绝大多数图像水印嵌入算法都是针对灰度图像的，直接用于彩色载体图像的数字水印算法较少[18-19].即使原始载体是彩色图像，大部分方法也只是通过提取其亮度信息或使用单色通道信息嵌入数字水印[16-17,20-21]，由于其未能很好体现和保留不同色彩分量在整个颜色空间内的特定联系，故必然影响数字水印的鲁棒性和不可感知性.文献[22]提出了一种彩色图像四元数频域幅值调制水印算法，该算法首先对原始载体图像进行分块四元数傅里叶变换，然后将数字水印嵌入到傅里叶直流分量的模值中.由于算法将水印带来的误差扩散到红、绿、蓝3色图像分量上，故可获得较好的抗常规信号处理能力.盖琦[23]将离散四元数余弦变换理论引入到彩色图像水印领域，并提出了一种基于离散四元数余弦变换的彩色图像水印新方法，获得了较好的抵抗JPEG压缩能力，并对叠加噪声、尺度缩放等攻击有一定的鲁棒性.Tsui等人[24]提出了基于多维傅里叶变换的非盲彩色图像水印算法，尽管该算法考虑了不同色彩分量间的特定联系，但因其忽略了多维傅里叶变换系数间的对称特性及数字水印的同步问题，导致数字水印的不可感知性与抗几何攻击能力均较差.王丹[25]给出了基于Pauli算符与欧拉公式的双侧四元数傅里叶变换求解过程，并提出了基于极坐标映射关系的笛卡尔坐标系彩色图像数字水印算法，该算法选取中频环形区域作为嵌入位置，同时采用传统加性原则嵌入水印信息，但其只能抵抗中轻度信号处理和几何攻击.陈北京等人[26]定义了四元数调制重叠变换(MQLT)，分析了MQLT系数的对称特性，同时结合MQLT变换及其系数对称特性，提出了一种鲁棒的双彩色图像盲水印算法，具有较好的不可感知性和对常规信号处理的鲁棒性.Tsougenis等人[27]以传统Tchebichef矩、Krawtchouk矩理论为基础，结合可反映色彩分量间联系的四元数技术，构造了四元数图像矩并据此提出了自适应彩色图像水印方法，但因Tchebichef矩和Krawtchouk矩不同程度存在图像描述与重建能力较差、对噪声较为敏感、数值计算稳定性较差等不足，导致整个图像水印系统工作性能并不理想.

鉴于此，本文以性能优良的指数矩理论为基础(图像描述与重建能力强、噪声敏感性低、数值计算稳定等)，结合基于四元数的彩色像素矢量整体处理技术，将传统灰度图像指数矩理论拓展推广至四元数层面，定义推导了适合于彩色图像的高精度四元数指数矩，构造了适合于彩色图像的四元数指数矩几何不变量，并进一步提出了基于四元数指数矩的抗几何攻击彩色图像水印方案.

1四元数与指数矩简介

1.1彩色图像的四元数描述

四元数可看成是复数的推广，并以高维度形式呈现.早在1843年英国数学家Hamilton[28]就提出了四元数理论，但是直到20世纪90年代四元数的理论和方法才被英国科学家Sangwine应用到彩色图像处理中.

对于大小为M×N的彩色图像，用f(x,y)表示图像中的一个像素，x和y分别为像素所在矩阵的行和列的位置，x∈[1,M]，y∈[1,N].令四元数的3个虚部分别代表彩色图像的R，G，B三个分量，实部为0，则四元数可以把在三色空间上的彩色图像视为一个矢量整体进行描述，即彩色图像f(x,y)可以表示为如下的无实部纯虚四元数：

(1)

其中，fR(x,y)，fG(x,y)，fB(x,y)是对应彩色图像的R，G，B三个分量，i，j，k为虚数单位.

显然，相对于传统的单色通道或提取亮度图像后再处理的方法而言，基于四元数的彩色图像处理更能体现出彩色图像的整体性，彩色图像的颜色信息能够得到很好的保持.

1.2指数矩基本理论

孟敏等人[29]于2011年提出的指数矩，能够很容易地构造出图像的高阶矩和低阶矩，并可以使用较少的矩来重建图像.与Legendre矩、Zernike矩、伪Zernike矩、Tchebichef矩、Krawtchouk矩等相比，指数矩不仅具有良好的图像描述能力，而且具有基函数简单、计算复杂度低、对噪声不敏感、数值计算稳定等特点，故可广泛应用于模式识别、信息检索与分类、数字水印等诸多领域.

在极坐标系(r,θ)中，阶数为n，重复度为m的指数矩Enm可定义为

(2)

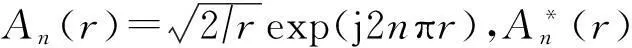
根据正交完整函数系理论，图像可以用无限的正交函数序列重建.使用有限数目的指数矩可以近似重建原图像函数f(r,θ)，并且所用项数越多，其近似程度越高.若已知图像最高阶nmax、最大重复度mmax的指数矩，则由其完备性和正交性，可得原始图像的重构公式：

(3)

2彩色图像的四元数指数矩

为便于全面刻画与描述彩色图像特征，我们这里将传统灰度图像的指数矩理论推广到四元数层面，并进一步定义出彩色图像的四元数指数矩.假设f(r,θ)为极坐标系下的彩色图像，则根据传统灰度图像的指数矩定义及四元数理论，我们可以定义彩色图像四元数指数矩(quaternion exponent moments, QEMs)[30-31]为

(4)

其中，μ是一个单位纯四元数，在此选择μ=(i+j+k)(r)表示径向基函数An(r)的共轭，且有：

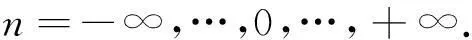
(5)

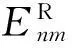
(6)

2.1四元数指数矩与传统指数矩之间的关系

1) 四元数指数矩分解与传统指数矩分解之间的关系

假设fR，fG，fB分别表示彩色图像的R，G，B三个分量，Enm(fR)，Enm(fB)，Enm(fG)分别表示彩色图像R，G，B三个分量的传统指数矩，Re(p)表示取复数p的实部，Im(p)表示取复数p的虚部，则四元数指数矩分解与传统指数矩分解之间的关系可以表示为

(7)

其中：

(8)

2) 四元数指数矩重构与传统指数矩重构之间的关系

根据四元数傅里叶变换及其逆变换理论[28]，四元数指数矩的重构过程可描述如下：

(9)

其中：

(10)

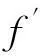
(11)

2.2四元数指数矩与传统指数矩之间的区别

四元数指数矩与传统指数矩之间的区别主要体现在2个方面:

1) 对于传统指数矩Enm=Anm+iBnm，其关于中心对称位置的指数矩为E-n-m=A-n-m+iB-n-m，其满足Anm=A-n-m,Bnm=-B-n-m，即Enm和E-n-m是一组共轭复数[29].

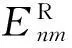
2) 由 1)知，传统指数矩的幅值满足|Enm|=|E-n-m|，即传统指数矩幅值是关于中心对称的[29]；

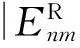
显然，进行数字水印嵌入时，应充分考虑上述四元数指数矩分布特点，以提高系统的不可感知性能.

图1给出了128×128×24 b真彩色图像Lena和Barbara的四元数指数矩重构图像及相应的重构误差.其中，由左至右，依次为阶数为5，10，20，30，40，50的四元数指数矩重构图像及相应的重构误差.

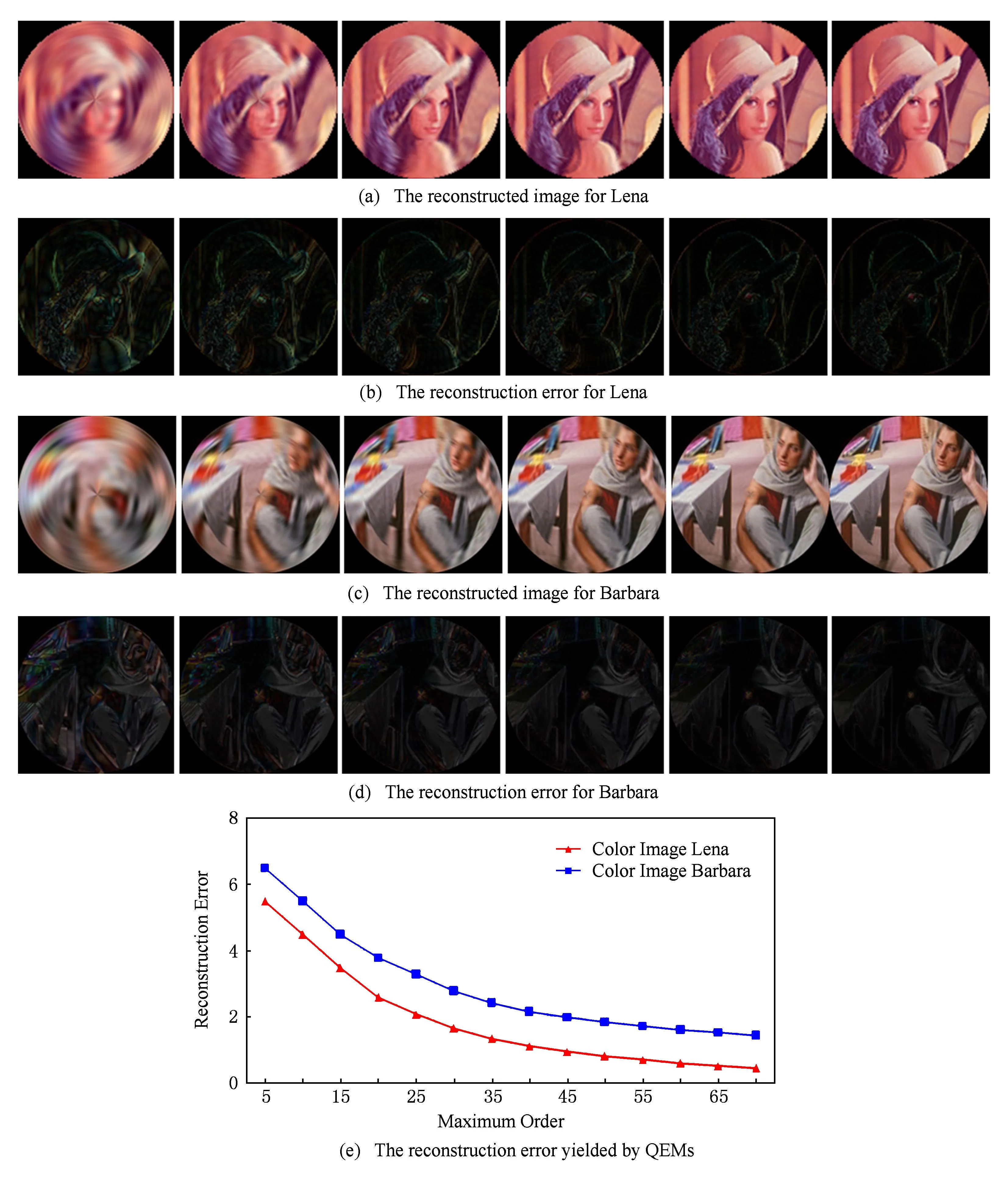
Fig. 1　The reconstructed images and reconstruction errors.图1　四元数指数矩的重构图像及相应的重构误差

3四元数指数矩的几何不变特性分析

下面我们来详细分析与讨论四元数指数矩的几何不变特性[30-32].

3.1四元数指数矩的平移不变性

四元数指数矩的平移不变性是通过几何矩实现的.对于一幅彩色图像，我们可以首先计算其质心，而彩色图像的质心坐标可通过零阶几何矩和一阶几何矩得到，即彩色图像的质心(xc,yc)为

(12)

其中，m0,0(fR)，m1,0(fR)，m0,1(fR)是颜色分量R的零阶和一阶几何矩，m0,0(fG)，m1,0(fG)，m0,1(fG)是颜色分量G的零阶和一阶几何矩，m0,0(fB)，m1,0(fB)，m0,1(fB)是颜色分量B的零阶和一阶几何矩.

待获得彩色图像的质心坐标(xc,yc)以后，我们可以先将彩色图像中心移到彩色图像的质心坐标，而后再计算彩色图像的四元数指数矩，此时四元数指数矩就具有了平移不变性.

3.2四元数指数矩的旋转不变性

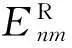
(13)

对式(13)两端取模，可得：

(14)

可见，旋转后彩色图像四元数指数矩的模与原彩色图像四元数指数矩的模是相等的，也就是说彩色图像四元数指数矩的模具有旋转不变特性.

3.3四元数指数矩的缩放不变性

我们可首先将彩色图像归一化到单位圆内，然后再计算彩色图像四元数指数矩，此时所计算得到的彩色图像四元数指数矩具有缩放不变性.对于一个给定的彩色图像函数g(r′,θ)，找到彩色图像的半径k，则r′的变化范围为0≤r′≤k，其归一化彩色图像函数可表示为

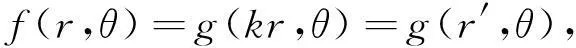
(15)

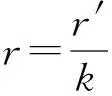
图2给出了四元数指数矩(幅值)的抗几何攻击能力测试结果(128×128×24 b真彩色图像Lena).这里，所测试的几何攻击包括旋转、缩放、平移、缩放旋转联合等.实验结果表明，彩色图像的四元数指数矩具有良好的几何不变特性.

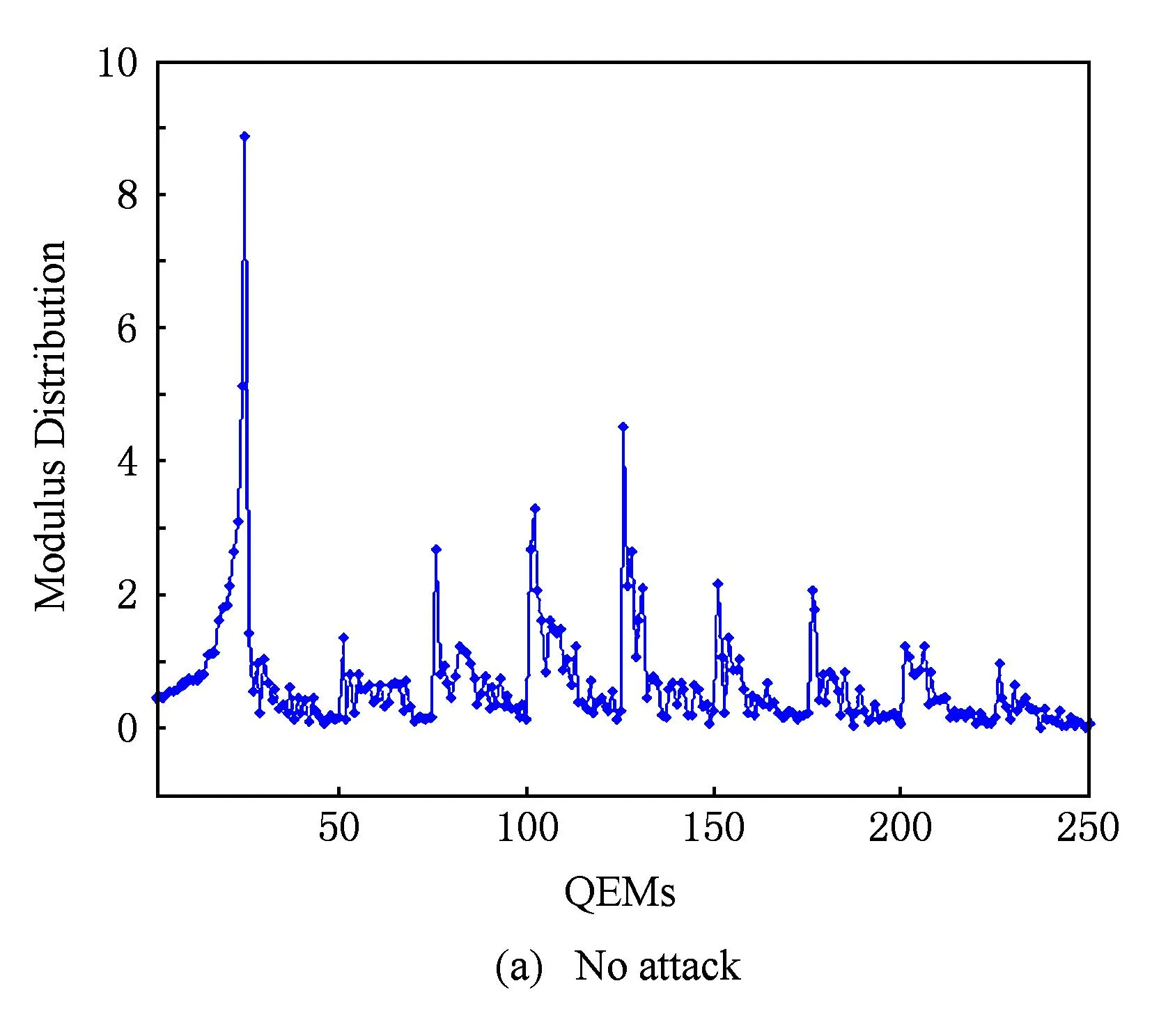
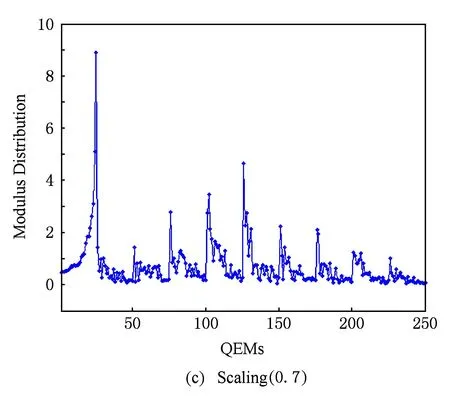
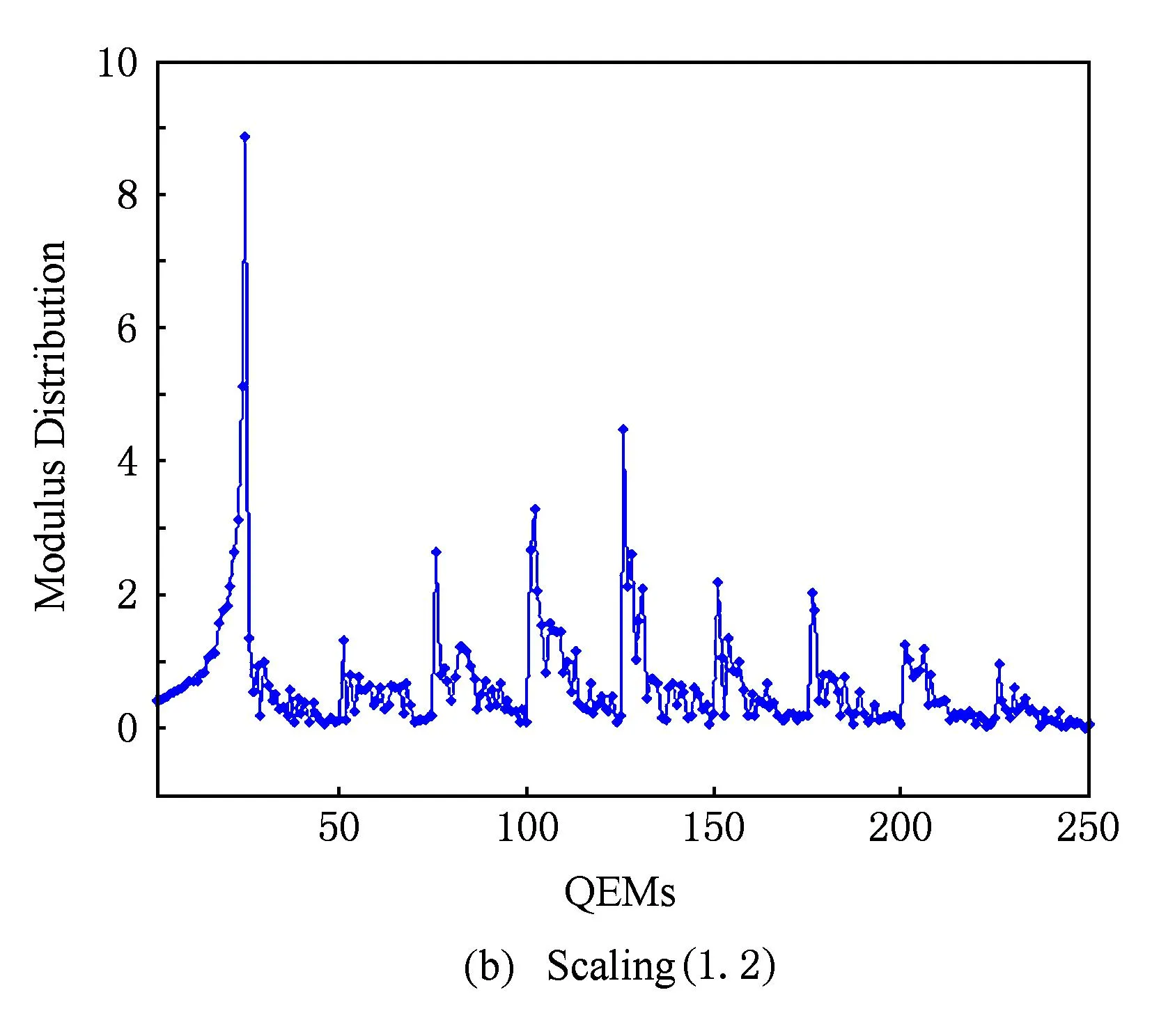
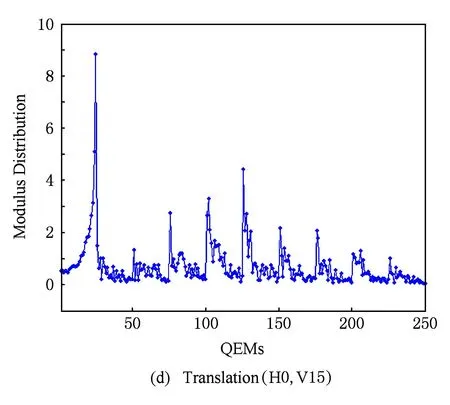
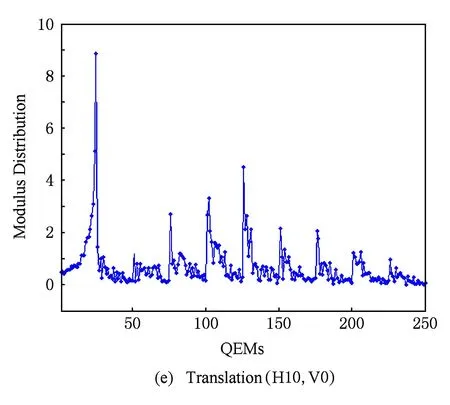
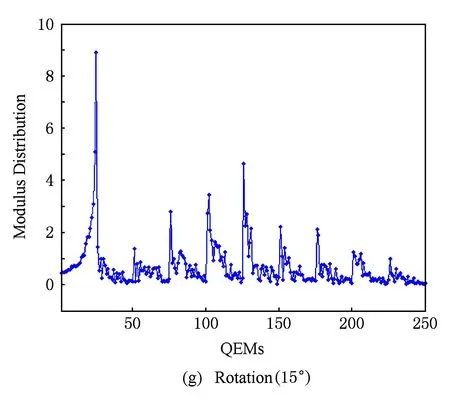
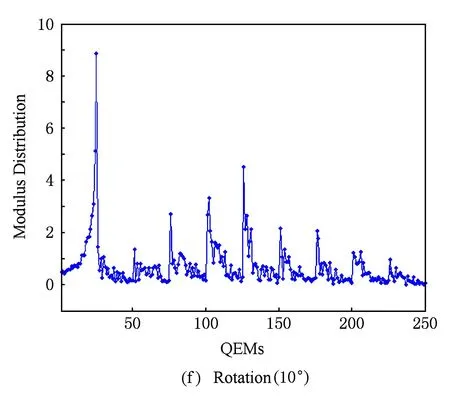
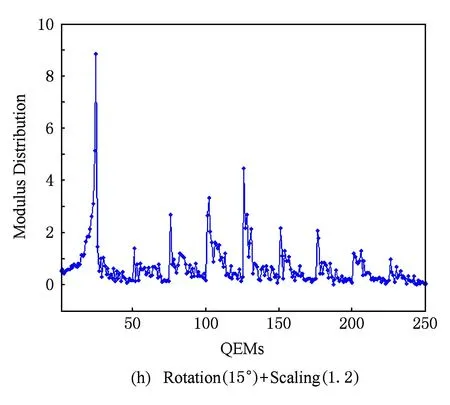
Fig. 2The modulus distribution of QEMs for color image Lena under various attacks.
图2四元数指数矩(幅值)的抗几何攻击能力测试(真彩色图像Lena)

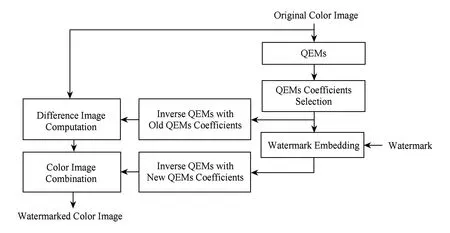
Fig. 3　Watermark embedding.图3　数字水印的嵌入原理

4抗几何攻击彩色图像水印

4.1基于四元数指数矩的彩色图像水印嵌入

本文将以性能优良的四元数指数矩为基础，提出一种可有效抵抗几何攻击的彩色图像水印新方案，其基本工作原理为：首先结合四元数指数矩的几何不变特性，计算出原始彩色图像的四元数指数矩，然后选取部分低阶四元数指数矩，并采纳量化调制策略将水印信息嵌入到四元数指数矩幅值中.图3给出了数字水印嵌入算法的系统框图.

设原始载体为24 b真彩色图像F={f(x,y),1≤x≤M,1≤y≤N}.其中，f(x,y)表示原始载体图像第x行、第y列像素的颜色值.

数字水印为二值图像W={w(i,j),1≤i≤P,1≤j≤Q}.其中，w(i,j)∈{0,1}代表二值水印图像的第i行、第j列像素值.则整个彩色图像水印的嵌入过程(关键步骤)可描述如下:

1) 数字水印的预处理

为了消除二值水印图像的像素空间相关性，提高整个数字水印系统的安全性能，确保彩色图像某一部分受到破坏后仍能全部或部分地恢复水印，宜首先对二值水印图像进行置乱加密.为此，本文首先引入Arnold变换，对二值水印图像W进行置乱加密并进一步将置乱后水印图像转换成一维数字水印W1，其中:

2) 四元数指数矩的计算

对原始彩色载体图像进行归一化处理，并计算出归一化彩色图像的四元数指数矩.参见第2节.

3) 低阶四元数指数矩的选取

大量仿真实验结果表明：面对滤波、叠加噪声、JPEG压缩等常规信号处理，部分四元数指数矩存在微小的计算误差.也就是说，必须合理选择四元数指数矩用于水印嵌入.为此，本文结合滤波、叠加噪声、JPEG压缩等常规信号处理实验，确定了如下稳定四元数指数矩(本文指攻击前后矩幅值变化小于2%的四元数指数矩为稳定四元数指数矩)选取规则：

①n≤0且m=0；

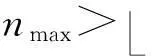
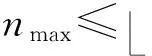
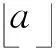
图4给出了512×512真彩色图像的稳定四元数指数矩选取示意图(这里四元数指数矩的最高阶nmax=31).其中，阴影部分所覆盖的区域即为稳定四元数指数矩所在区域.

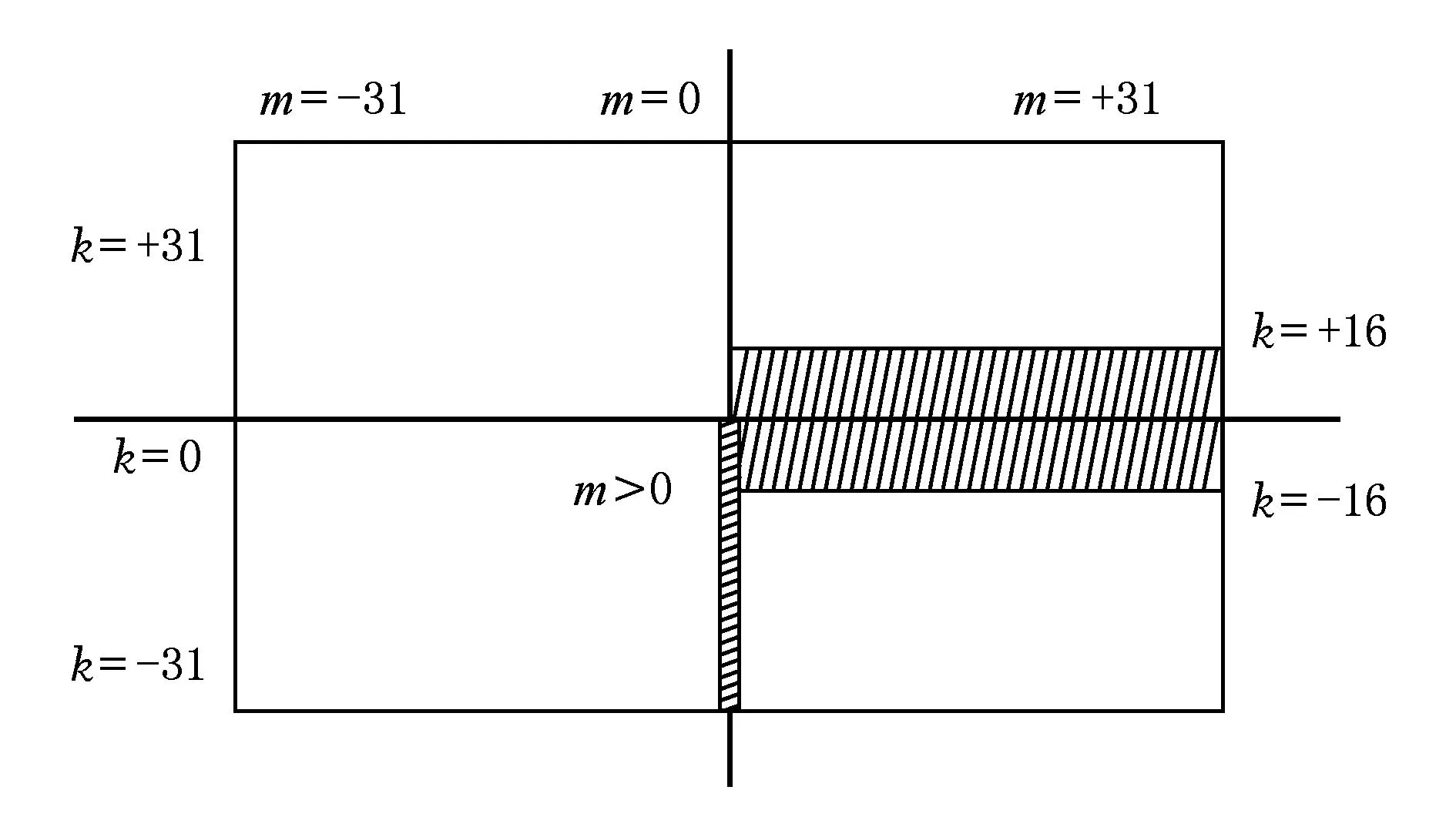
Fig. 4　Robust QEMs selection.图4　稳定四元数指数矩选取示意图

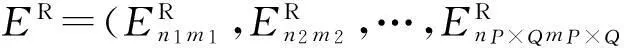
4) 数字水印的嵌入

本文采用量化调制四元数指数矩幅值的方法嵌入数字水印信息，量化规则如下：

(16)

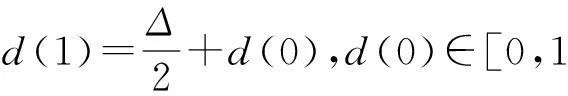
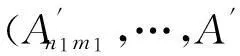
5) 含水印彩色图像的生成

① 计算出含水印归一化彩色图像，其由2部分合并而成：

部分1是未被修改的四元数指数矩所重构的彩色图像f*(x,y)：

(17)

这里，fO(x,y)是原始载体的归一化彩色图像，fW(x,y)是待修改四元数指数矩的重构部分彩色图像，重构方法见第2节.

部分2是已修改四元数指数矩的重构部分彩色图像fW′(x,y)，重构方法见第2节.

将上面2部分合并，即得到含水印归一化彩色图像f′(x,y)：

(18)

② 对含水印归一化彩色图像f′(x,y)进行逆归一化处理，即可得到含水印彩色图像F′.

4.2基于四元数指数矩的彩色图像水印提取

本文讨论的彩色图像水印检测算法属于目标检测算法，即在检测数字水印时不需要原始的载体图像.设待检测彩色图像为F′，则数字水印检测过程(关键步骤)可描述如下:

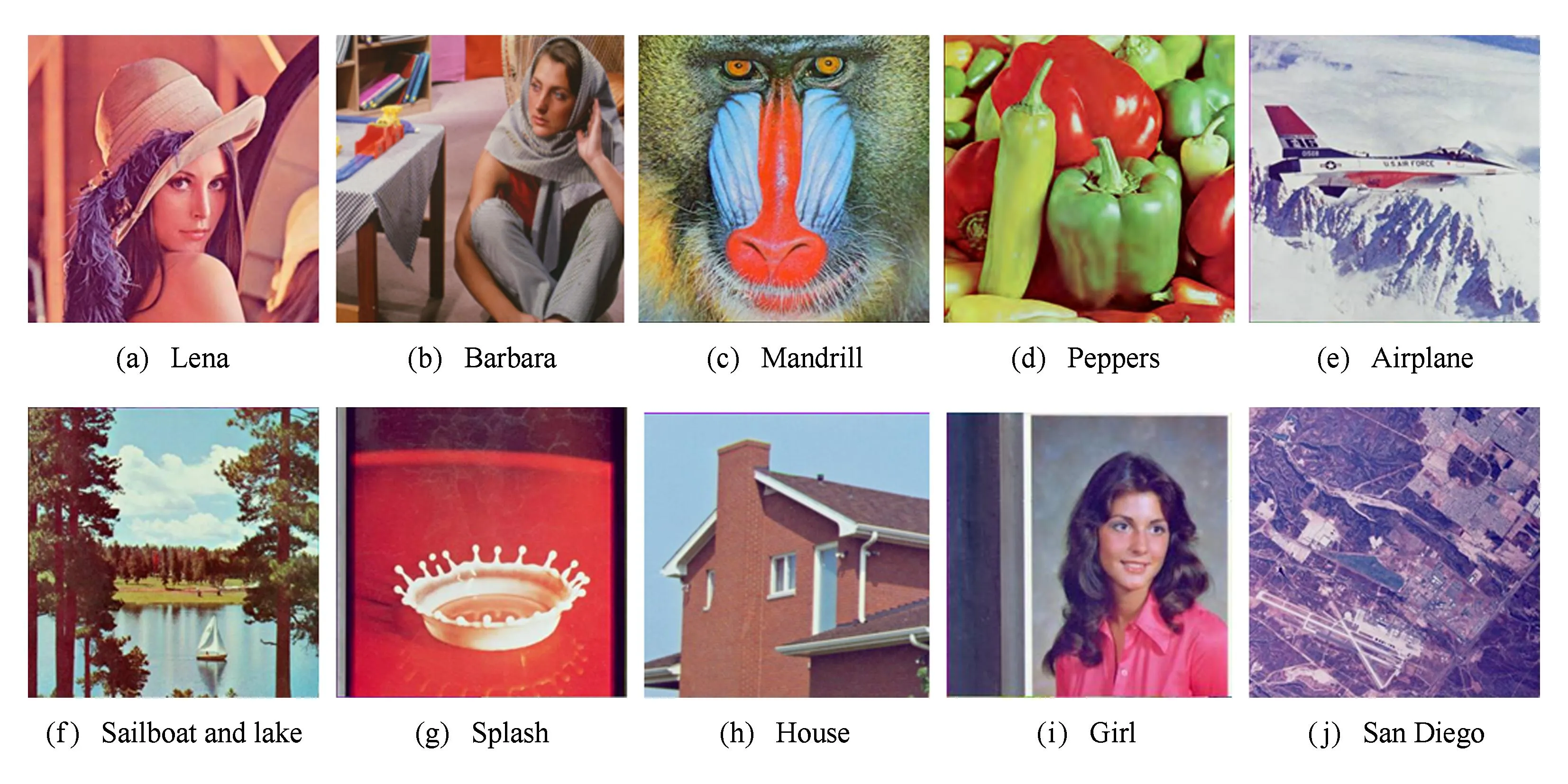
Fig. 5　The host color images.图5　原始彩色载体图像

1) 对待检测彩色图像F′进行归一化处理，并计算出归一化彩色图像的四元数指数矩.详见第2节.

2) 利用密钥Key1选择P×Q个四元数指数矩

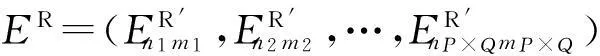
3) 数字水印提取.

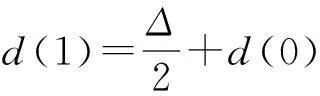
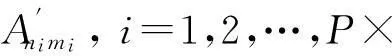
(19)

(20)

其中，i=1,2,…,P×Q,式(20)可以分解为3个具体步骤:

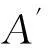
Ⅱ 计算Ⅰ中2个距离的差值，记为t=dis0-dis1；

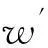
5仿真实验与结论

为了验证本文彩色图像水印算法的高效性，以下分别给出了不可感知性能测试、抗攻击(包括常规信号处理和几何攻击)能力测试的实验结果，并与图像归一化算法[17]、线性判别分析算法[20]、SVM分类算法[21]进行了对比.实验中，所选用的原始载体分别为256×256×24 b真彩色标准图像“Lena”,“Barbara”,“Mandrill”,“Peppers”,“Airplane”,“Sailboat and lake”,“Splash”,“House”,“Girl”,和“San Diego”，数字水印采用了16×16的二值图像，如图5和图6所示.另外，量化步长Δ=0.5.这里，我们使用了比特失真率BER和峰值信噪比PSNR来衡量数字水印算法的工作性能，BER和PSNR定义如下：

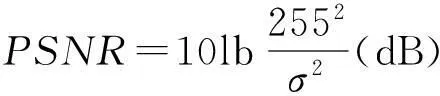
(21)

其中,F(i,j)和F′(i,j)分别为原始彩色载体图像和含水印彩色图像，M,N为图像大小.

Fig. 6　Digital watermark.图6　数字水印

5.1不可感知性能测试

表1给出了4种彩色图像水印方法的不可感知性能测试结果.图7分别给出了图像归一化算法[17]及本文算法的含水印彩色图像Lena，Barbara和Mandrill.图8分别给出了图像归一化算法[17]及本文算法的差值图像(原始彩色载体和含水印彩色图像的差值图像).

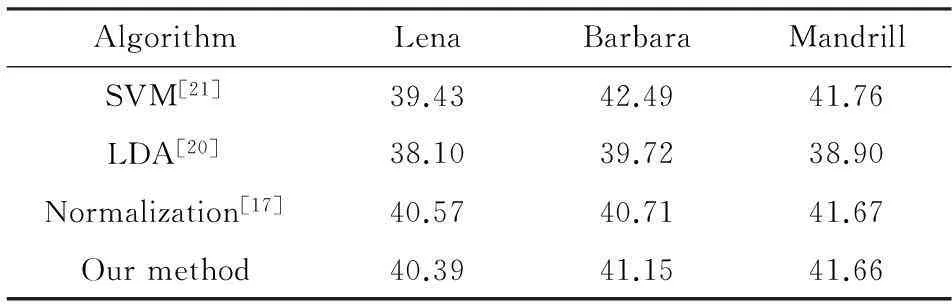
Table 1　The PSNR for Various Watermarking Method

Fig. 7　The watermarked images using different algorithms.图7　不同彩色图像水印方法的含水印图像

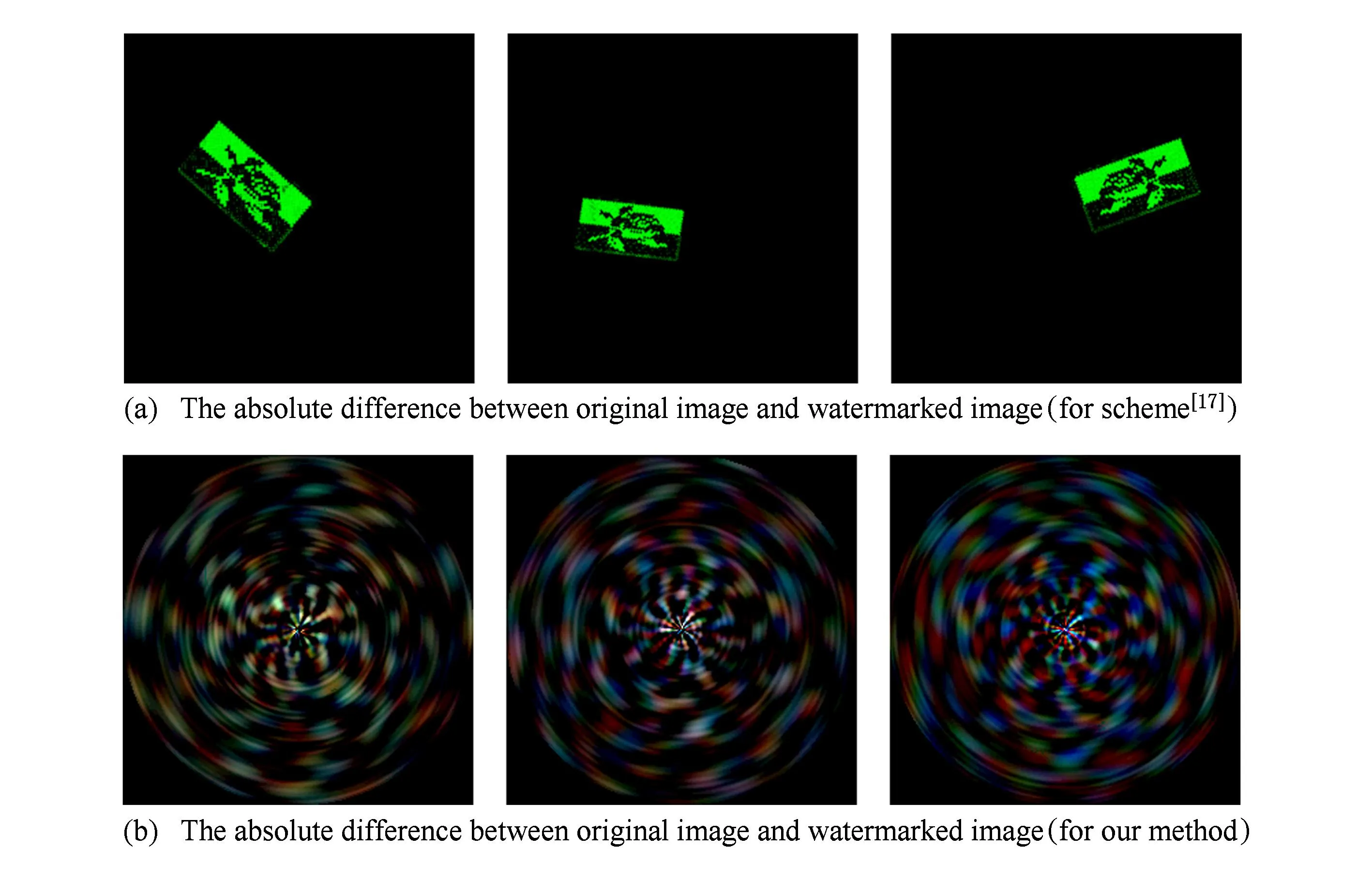
Fig. 8　The absolute difference images for different algorithms.图8　不同彩色图像水印方法的差值图像

5.2抗攻击能力测试

为了检测本文算法的鲁棒性能，仿真实验分别对图像归一化算法[17]、线性判别分析算法[20]、SVM分类算法[21]及本文算法的含水印彩色图像进行了一系列攻击.

图9给出了本文算法的部分数字水印检测结果(在常规信号处理和几何攻击下).在完全相同的实验环境和条件下，表2和表3分别给出了4种彩色图像水印方法的抗攻击能力对照结果(失真率BER).

Fig. 9　The attacked watermarked image and the extracted watermark.图9　本文算法的部分数字水印检测结果(在常规信号处理和几何攻击下)

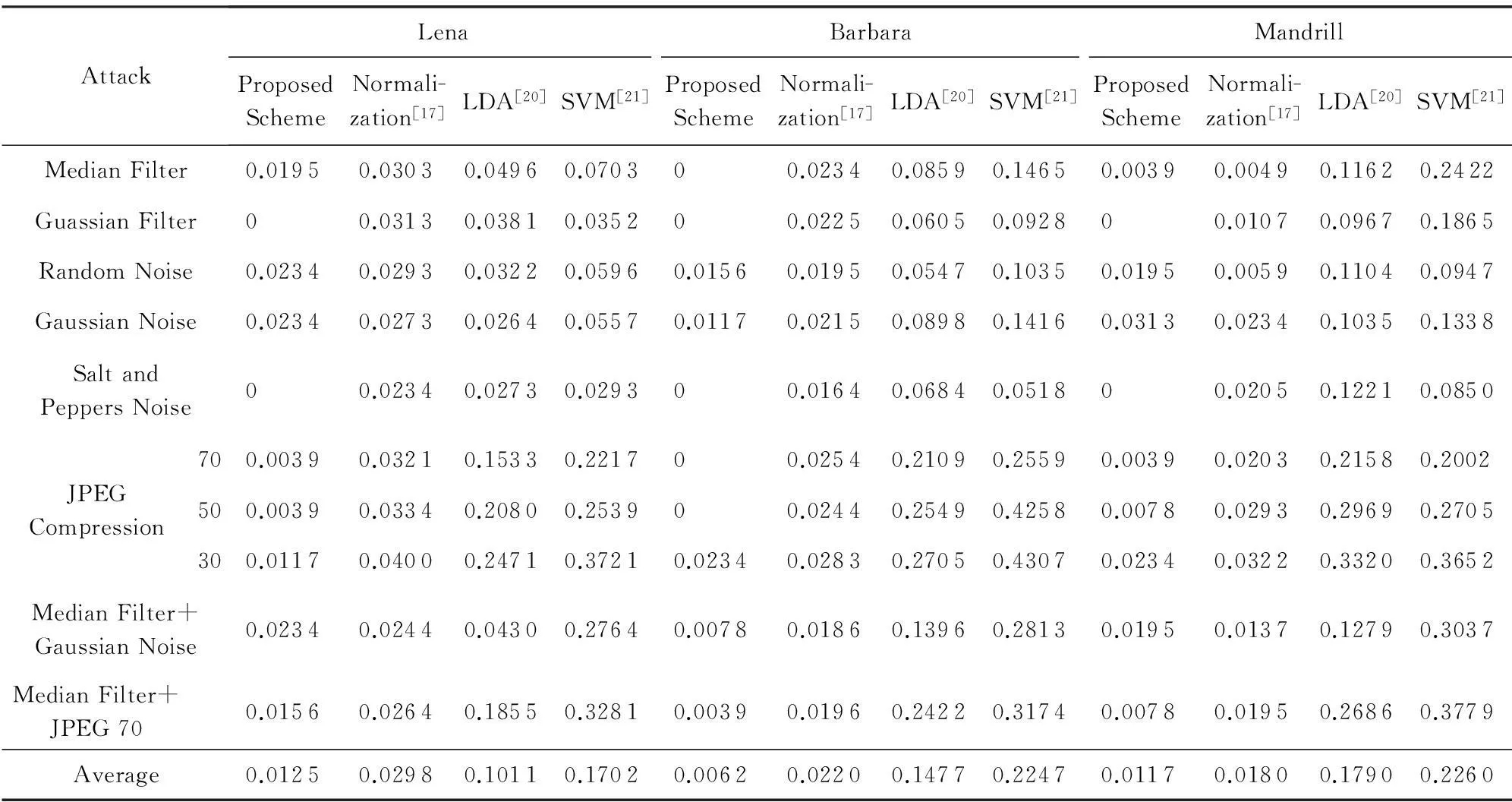
AttackLenaBarbaraMandrillProposedSchemeNormali-zation[17]LDA[20]SVM[21]ProposedSchemeNormali-zation[17]LDA[20]SVM[21]ProposedSchemeNormali-zation[17]LDA[20]SVM[21]MedianFilter0.01950.03030.04960.070300.02340.08590.14650.00390.00490.11620.2422GuassianFilter00.03130.03810.035200.02250.06050.092800.01070.09670.1865RandomNoise0.02340.02930.03220.05960.01560.01950.05470.10350.01950.00590.11040.0947GaussianNoise0.02340.02730.02640.05570.01170.02150.08980.14160.03130.02340.10350.1338SaltandPeppersNoise00.02340.02730.029300.01640.06840.051800.02050.12210.0850JPEGCompression700.00390.03210.15330.221700.02540.21090.25590.00390.02030.21580.2002500.00390.03340.20800.253900.02440.25490.42580.00780.02930.29690.2705300.01170.04000.24710.37210.02340.02830.27050.43070.02340.03220.33200.3652MedianFilter+GaussianNoise0.02340.02440.04300.27640.00780.01860.13960.28130.01950.01370.12790.3037MedianFilter+JPEG700.01560.02640.18550.32810.00390.01960.24220.31740.00780.01950.26860.3779Average0.01250.02980.10110.17020.00620.02200.14770.22470.01170.01800.17900.2260

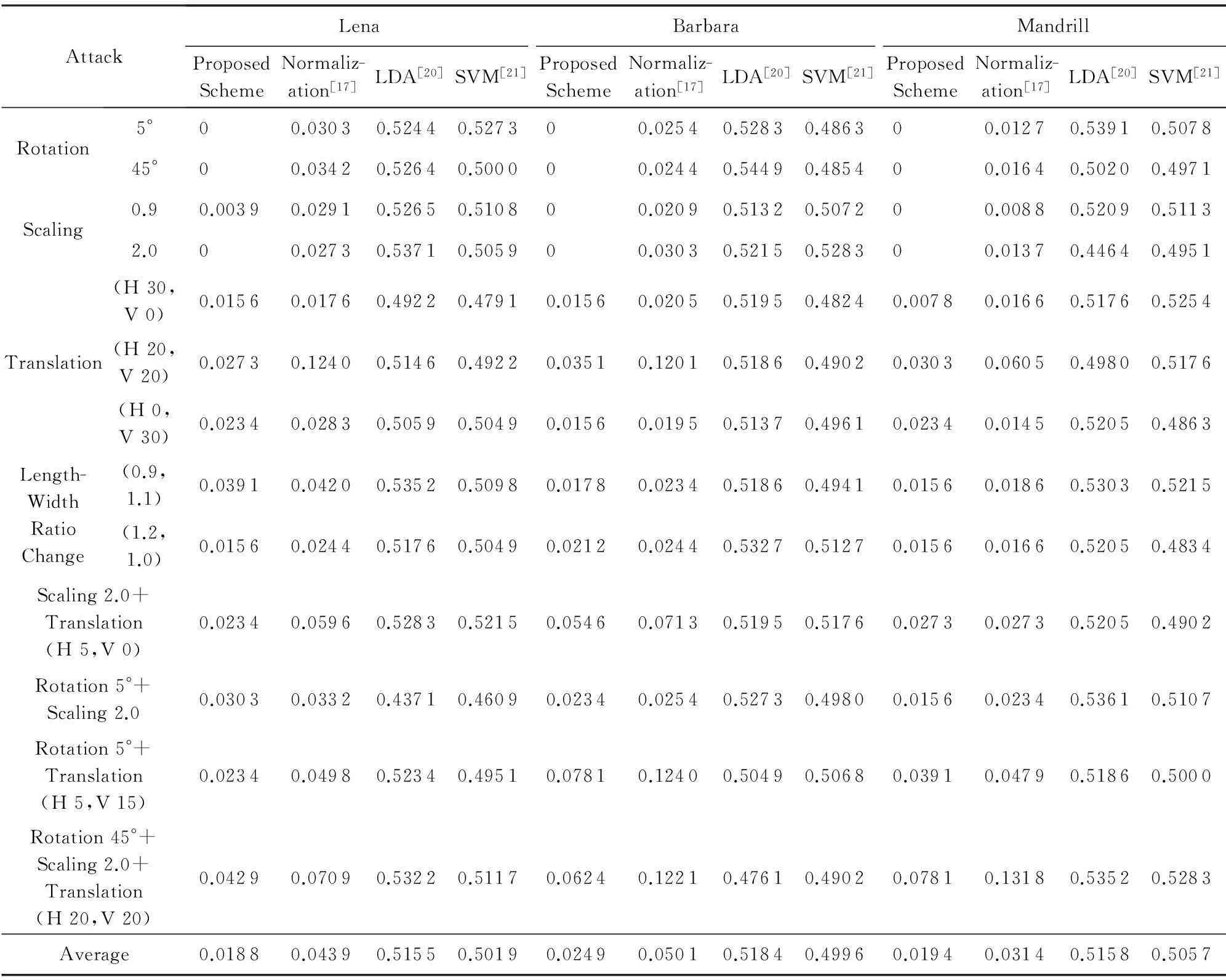
Table 3　The Watermark Detection Results for Geometric Distortions (BER)

实验结果表明:本文所提出的彩色图像水印算法不仅具有较好的不可感知性，而且对常规信号处理和几何攻击均具有较好的鲁棒性，整体工作性能明显优于图像归一化、线性判别分析、SVM分类等彩色图像水印方案，其原因在于本文采用了性能稳定的四元数指数矩不变量嵌入水印.

6结束语

本文以传统的四元数理论与指数矩理论为基础，定义推导了可全面反映色彩分量间内在联系的彩色图像四元数指数矩，分析了彩色图像四元数指数矩的不变特性，并据此提出了一种基于四元数指数矩的抗几何攻击彩色图像水印算法.同时，仿真实验结果也说明了本文算法的有效性.

特别需要指出的是:本文所定义推导的彩色图像四元数指数矩可广泛应用于彩色图像识别、分类、检索等诸多领域，故具有较大的应用价值.

参考文献

[1]Marco B, Davide C, Victor P. Protecting the content integrity of digital imagery with fidelity preservation: An improved version[J]. ACM Trans on Multimedia Computing, Communications, and Applications, 2014, 7(3): Article 15

[2]Cheddad A, Condell J, Curran K. Digital image steganography: survey and analysis of current methods[J]. Signal Processing, 2010, 90(3): 727-752

[3]Bianchi T, Piva A. Secure watermarking for multimedia content protection: a review of its benefits and open issues[J]. IEEE Signal Processing Magazine, 2013, 30(2): 87-96

[4]Mathon B, Cayre F, Bas P, et al. Optimal transport for secure spread-spectrum watermarking of still images[J]. IEEE Trans on Image Processing, 2014, 23(4): 1694-1705

[5]Li M, Michel K K, Dimitris A P. Extracting spread-spectrum hidden data from digital media[J]. IEEE Trans on Information Forensics and Security, 2013, 8(7): 1201-1209

[6]Yang H Y, Wang X Y, Wang C P. A robust digital watermarking algorithm in undecimated discrete wavelet transform domain[J]. Computers & Electrical Engineering, 2013, 39(3): 893-906

[7]Zhang H, Shu H, Coatrieux G. Affine legendre moment invariants for image watermarking robust to geometric distortions[J]. IEEE Trans on Image Processing, 2011, 20(8): 2189-2199

[8]Lou Oujun, Wang Zhengxuan. A contourlet-domain watermarking algorithm against geometric attacks based on feature template[J]. Chinese Journal of Computers, 2009, 32(2): 308-317 (in Chinese)(楼偶俊, 王钲旋. 基于特征点模板的Contourlet域抗几何攻击水印算法研究[J]. 计算机学报, 2009, 32(2): 308-317)

[9]Su P, Chang Y, Wu C. Geometrically resilient digital image watermarking by using interest point extraction and extended pilot signals[J]. IEEE Trans on Information Forensics and Security, 2013. 8(12): 1897-1908

[10]Yuan X C, Pun C M, Chen P C L. Geometric invariant watermarking by local Zernike moments of binary image patches[J]. Signal Processing, 2013, 93(7): 2087-2095

[11]Kang X G, Huang J W, Zeng W J. Efficient general print-scanning resilient data hiding based on uniform log-polar mapping[J]. IEEE Trans on Information Forensics & Security, 2010, 5(1): 1-12

[12]Zhu H Q, Liu M, Li Y. The RST invariant digital image watermarking using Radon transforms[J]. Digital Signal Processing, 2010, 20(6): 1612-1628

[13]Papakostas G A, Koulouriotis D E, Tourassis V D. Performance evaluation of moment-based watermarking methods: A review[J]. Journal of Systems and Software, 2012, 85(8): 1864-1884

[14]Coatrieux G, Pan W, Cuppens-Boulahia N. Reversible watermarking based on invariant image classification and dynamic histogram shifting[J]. IEEE Trans on Information Forensics and Security, 2013, 8(1): 111-120

[15]Bhatnagar G, Wu Q M, Atrey P K. Secure randomized image watermarking based on singular value decomposition[J]. ACM Trans on Multimedia Computing, Communications, and Applications (TOMCCAP), 2013, 10(1): Article 4

[16]Su Q, Niu Y, Zou H, et al. A blind dual color images watermarking based on singular value decomposition[J]. Applied Mathematics and Computation, 2013, 219(16): 8455-8466

[17]Niu P P, Wang X Y, Yang Y P, et al. A novel color image watermarking scheme in nonsampled contourlet-domain[J]. Expert Systems with Applications, 2011, 38(3): 2081-2098

[18]Moghaddam M E, Nemati N A. A robust color image watermarking technique using modified imperialist competitive algorithm[J]. Forensic Science International, 2013, 233(1): 193-200

[19]Chou C H, Liu K C. A perceptually tuned watermarking scheme for color images[J]. IEEE Trans on Image Processing, 2010, 19(11): 2966-2982

[20]Fu Y G, Shen R M. Color image watermarking scheme based on linear discriminant analysis[J]. Computer Standard & Interfaces, 2008, 30(3): 115-120

[21]Tsai H H, Sun D W. Color image watermark extraction based on support vector machines[J]. Information Sciences, 2007, 177(2): 550-569

[22]Sun Jing, Yang Jingyu, Fu Desheng. Watermarking algorithm for color images based on quaternion frequency modulation[J]. Computer Science, 2011, 38(3): 123-126 (in Chinese)(孙菁, 杨静宇, 傅德胜. 彩色图像四元数频域幅值调制水印算法[J]. 计算机科学, 2011, 38(3): 123-126)

[23]Gai Qi. Color image information hiding technology based on quaternion theory[D]. Tianjin: Nankai University, 2009 (in Chinese)(盖琦. 基于四元数理论的彩色图像信息隐藏技术[D]. 天津: 南开大学, 2009)

[24]Tsui T K, Zhang X P, Androutsos D. Color image watermarking using multidimensional Fourier transforms[J]. IEEE Trans on Information Forensics and Security, 2008, 3(1): 16-28

[25]Wang Dan. Research on quaternion Fourier transform and digital watermarking[D]. Changchun: Jilin University, 2013 (in Chinese)(王丹. 四元数傅立叶变换及数字水印算法研究[D]. 长春: 吉林大学, 2013)

[26]Chen Beijing, Tian Cuicui, Dai Hui, et al. Modulated quaternion lapped transform and its application in dual color image watermarking[J]. Journal of Southeast University: Natural Science Edition, 2013, 43(6): 1195-1202 (in Chinese)(陈北京, 田翠翠, 戴慧, 等. 四元数调制重叠变换及其在双彩色图像数字水印中的应用[J]. 东南大学学报: 自然科学版, 2013, 43(6): 1195-1202)

[27]Tsougenis E D, Papakostas G A, Koulouriotis D E, et al. Adaptive color image watermarking by the use of quaternion image moments[J]. Expert Systems with Applications, 2014, 41(14): 6408-6418

[28]Hamilton W R. Elements of Quaternions[M]. London: Longmans Green, 1866

[29]Meng Min, Ping Ziliang. Decompose and reconstruct images based on exponential-Fourier moments[J]. Journal of Inner Mongolia Normal University: Natural Science Edition, 2011, 40(3): 258-260 (in Chinese)(孟敏, 平子良. 基于指数矩的图像分解和重建[J]. 内蒙古师范大学学报: 自然科学版, 2011, 40(3): 258-260)

[30]Chen B J, Shu H Z, Zhang H et al. Quaternion zernike moments and their invariants for color image analysis and object recognition[J]. Signal Processing, 2012, 92(2): 308-318

[31]Guo L Q, Zhu M. Quaternion Fourier-Mellin moments for color image[J]. Pattern Recognition, 2011, 44(2): 187-195

[32]Xin Y, Liao S, Pawlak S. Circularly orthogonal moments for geometrically robust image watermarking[J]. Pattern Recognition, 2007, 40(12): 3740-3752

Wang Xiangyang, born in 1965. Professor. His research interests include network information security, multimedia computing, and computer vision.

Yang Hongying, born in 1965. Professor. Her research interests include multimedia signal processing, pattern recognition, and multimedia security.

Niu Panpan, born in 1983. PhD, Lecturer. Her research interests include information hiding and digital watermarking.

Wang Chunpeng, born in 1988. PhD candidate. His research interests include image processing and digital watermarking.

中图法分类号TP309.2

基金项目：国家自然科学基金项目(61472171，61272416)

收稿日期：2014-11-04；修回日期：2015-03-26

This work was supported by the National Natural Science Foundation of China (61472171，61272416).