一种通用云计算资源调度问题的快速近似算法

魏　蔚　刘　扬　杨卫东

(河南工业大学信息科学与工程学院　郑州　450001)

(nsyncw@126.com)



一种通用云计算资源调度问题的快速近似算法

魏蔚刘扬杨卫东

(河南工业大学信息科学与工程学院郑州450001)

(nsyncw@126.com)

A Fast Approximation Algorithm for the General Resource Placement Problem in Cloud Computing Platform

Wei Wei, Liu Yang, and Yang Weidong

(CollegeofInformationScienceandEngineering,HenanUniversityofTechnology,Zhengzhou450001)

AbstractThere are regionally distributed demands for various resources in cloud based large-scale online services. Given fixed resource budget, the service providers need to decide where to place resources to satisfy massive demands from all regions, where demands are usually represented by mean value in given time span. However, in scenarios with a large number of resources, demands are dynamic and stochastic, considering fine-grained demands and adopting stochastic model will further improve resource utilization. Compared with mean demand-based algorithm, considering demand stochasticity in algorithm will increase resource utilization ratio, but also leads to high time complexity. The time complexity of optimal algorithm is linear to total amount of resources, thus may be inefficient when dealing with a large number of resources. Based on nonlinear programming theory, we propose Fast Resource Placement (FRP), an effective resource placement method of high efficiency. In the algorithm, optimal solution is represented by continuous functions of input, and we construct approximation functions to reduce the computation complexity. The preliminary experiments show that in scenarios with general settings, compared with optimal algorithm, FRP can reduce the computation time by three orders of magnitude, and can achieve 99% effect of optimal solution. Therefore, FRP can be used to schedule large number of resources efficiently in time-tense scheduling scenarios.

Key wordsstochastic demand; resource scheduling; resource placement; nonlinear programming; cloud computing

摘要在分布式云计算平台中，面向大规模用户的在线应用需处理针对海量资源的用户需求，在给定的资源预算下，服务提供商需确定最优资源放置位置，以最大程度地满足用户需求,通常需求用给定时间段内均值表示.然而真实场景中用户需求是高度动态和随机的，采用随机需求模型以考虑更多需求细节，资源利用率可得到进一步优化.但相比均值调度方法，随机需求模型会导致很高的计算复杂度.已有的最优解求解算法的时间复杂度和资源总量成正比，无法满足海量资源在线调度的效率要求.基于非线性规划理论，提出了一个快速资源分配算法，该算法可将计算复杂度降低至最优解算法的1‰，并逼近最优解效果的99%，因此可用于在线应用场景中海量资源的高效调度.

关键词随机需求；资源调度；资源放置；非线性规划；云计算

大规模在线服务系统(如YouTube[1]和Facebook[2])面临来自全球各个区域的高度动态的用户请求，可利用云计算平台降低费用并提升用户体验.在典型的分布式云计算平台中，需妥善分配资源到全球各个云数据中心以满足尽可能多的用户请求；且对于单个用户请求，倾向分发到较近的数据中心以提供较好的用户体验.

已有工作初步探讨了在上述场景中进行资源调度的若干问题.在流媒体分发的相关工作中，文献[3]深入分析了面向流处理服务的资源部署问题，考虑了经由中间节点响应客户请求的情况，采用集合覆盖等方法从多角度规约问题获取最优解.文献[4]分析了混合云中面向视频点播服务的资源配置问题，通过限制平均延时以保证服务质量，利用李雅普诺夫优化方法获得长时间范围内的统计平均最优.在内容分发网络研究方向上，文献[5]考虑利用空闲带宽分发容迟数据，通过延时调度充分复用带宽资源并减少平均分发时间，采用任务调度与资源整合相结合的思路.文献[6]中的MetaCDN架构将用户内容分发到多个不同的存储云中，最大化租用费用及服务质量相关的效用函数.文献[7]提出基于拉普洛夫优化理论的通用优化框架，在保证服务质量的前提下最小化操作费用.文献[8]研究了存储云中的内容存放问题，以及在存储云间的分发网络构建问题，并提出了多种启发式算法.文献[9]设计了一种结合树形和网状拓扑的新型混合分发架构，采用网络编码方法提高分发效率，保证服务质量同时可大幅降低骨干网流量.文献[10] 提出了基于用户行为特征的资源分配策略，通过统计用户工作习惯与任务完成时间期望值的变化规律，建立用户行为特征信息表，从而动态调整云计算系统的资源分配策略.文献[11]引入用户效用的概念，建立了云环境中用户效用的描述模型，给出了用户对任务执行时间和费用满意程度的量化方法，基于线性规划理论提出了云环境中面向用户效用的任务调度优化模型.除了高度相关的云计算方向研究工作，P2P领域中的相关工作也研究了类似的资源调度问题[12].

上述工作采用均值需求模型以保证调度算法效率，然而真实场景中用户需求是高度动态和随机的，通过考虑更多需求细节，采用随机需求模型，资源利用率可得到进一步优化.在均值模型中，资源需求通过给定调度时间间隔内资源需求量均值表示，参与运算的是代表均值的标量值；随机需求模型中，资源需求使用随机变量表示，参与运算的一般是需求的累积概率分布函数.文献[13-14]将基于随机需求的通用资源调度问题转化为最小费用最大流问题，并提出基于连续最短路径的最优解算法.其中，文献[13]的问题设定中，每区域有资源限制，目标是最大化满足的需求数量的期望值；文献[14]的问题设定中，没有区域资源限制，目标是资源费用和收益组合表示的整体代价最小化.但基于连续最短路径求解算法的复杂度与资源总量成正比例，无法满足大规模场景下实时快速调度的时间要求.

通过观察通用分配问题的内部结构，我们提出了快速近似算法，论文的创新点如下:1)证明该问题可转化为一个2阶段优化问题，可逐步快速求解；2)证明在每阶段的子问题中，最优结果均可表示为输入参数的函数，并给出函数的数学表达式；3)采用离散函数模拟算法中的连续函数，提出了快速近似算法.实验结果表明，该算法在达到最优解效果99%的情况下，时间复杂度可缩减至最优解算法的1‰.

1通用资源分配问题

对来自区域j的对i型资源的请求，若该请求被分配给资源i，则该请求被标记为“已满足”.一个来自区域j的i型资源的请求被满足，则将它分配到：1)位于区域j的i型资源，称之为本地满足；或2)位于其他区域的i型资源，称之为远程满足.若请求没有被分配到任何资源，则将其标记为“未满足”.

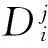
(1)

(2)

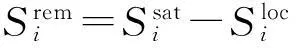
(3)

则方案P的i型收益期望值为

(4)

因对于任意连续的非负随机变量x与常量C有:

(5)

其中,cdfx(·)是x的累积概率分布函数，则式(4)中i型收益可转化为最终形式：

(6)

则所有i型收益的期望值的总和为总期望收益:

(7)

在通用的离线资源分配场景中，服务提供商通常会预订定量的全局资源(总量记为U)，有:

(8)

(9)

(10)

(11)

2快速资源分配算法

在典型的云计算系统中，通用离线资源调度问题的输入数据量会非常大，在常见场景中一般会有资源类型和区域数的乘积I×J≥104.为寻找高效的解决算法，我们首先研究最优解的特征，首先引入定理1.

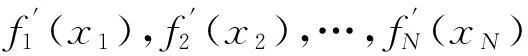
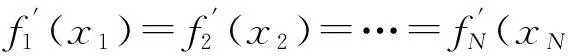
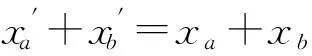
(12)

(13)

证毕.

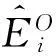
(14)

因为Li(1≤i≤I)对给定的类型配置方案O是常量，则根据定理1，可由以下方法找到{P}O中达到最大i型期望收益的资源配置方案P′.

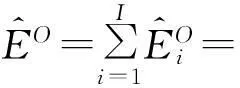
(15)

通过下述推论可找到限制U下的最优方案：

为得到最优算法，还需明确最优类型配置方案和最优配置方案间的内在关系，描述如下：

基于推论1至推论4，在构建需要的函数后，原问题可转化为2阶段优化问题并快速求解：阶段1中，对给定的全局限制U，根据推论2～3快速定位最优类型配置方案O′；阶段2中，根据推论1在 {P}O′中快速定位最优资源配置方案P′.由推论4可知，P′即为满足全局资源约束U的最优方案.

算法1. 快速资源分配算法FRP.

输入：需求累积分布函数cdfi(·),cdfi,j(·)及其反函数;资源总量U;参数Xi,j=min(cdfi,j(x)=1|∀x);

① FORi=1 toI

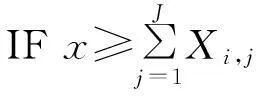
④ END IF

⑤ END FOR

⑥ FORk=0 toK

⑦v=wlockK;

⑧ FORi=1 toI

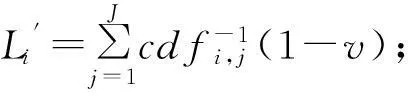
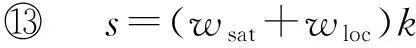
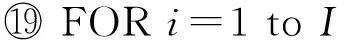
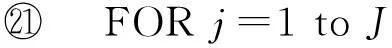
3实验

本文和文献[13]问题设定较接近，且文献[13]的求解方法具代表性，我们实现了文献[13]中基于连续最短路径(successive shortest path, SSP)的最优求解算法，命名为SSP-RP(SSP based resource placement).基于相同的实验设定，比较均值算法、SSP-RP和FRP的求解效果，并验证FRP求解效率和效果之间的关系.其中，实验图表涉及的比率型数据，均表示FRP方法收益与文献[13]中SSP-RP方法收益的比值.在实验设定中，随机用户需求符合Zipf分布(同文献[13])，即i型资源的平均需求占所有需求的比例如下：

(16)

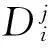
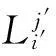
(17)

首先我们比较3种方法在不同Zipf参数下效果的变化趋势.参考文献[13]，实验设定如下：区域数量和资源数量分别是J=4和I=500，收益权值wloc=wsat=1，FRP的精度K=100，总请求量期望值λ=1 000.Zipf参数取较大范围，为0.7～1.4.实验中我们比较3种方法在资源盈余(U=1 500>λ)和资源不足(U=500<λ)情况下的效果，如图1和图2所示，在图1、图2中，横坐标为Zipf参数，纵坐标为期望收益.我们可看到在不同的Zipf参数下，FRP都要好于均值分配算法，且与SSP-RP算法的效果非常接近.

Fig. 1　Expected revenue with different Zipf values under deficit scenario.图1　资源不足时收益与Zipf的关系

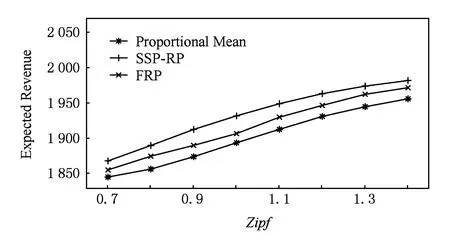
Fig. 2　Expected revenue with different Zipf values under surplus scenario.图2　资源盈余时收益与Zipf的关系

为明确资料类型数量I对算法的影响，我们还比较了3种方法的效果随资源类型数变化趋势，实验设定如下：资源数量分别是J=4和I=500，收益权值wloc=wsat=1，FRP的精度K=100，总请求量期望值λ=1 000，Zipf=1.0.同文献[13]，取I∈[100,1 000]，以涵盖不同数量级的资源数量.我们比较了I为100～1 000时3种算法的求解效果，如图3和图4所示，在不同的资源数量I下，FRP的效果也始终优于均值方法，和SSP-RP方法接近.

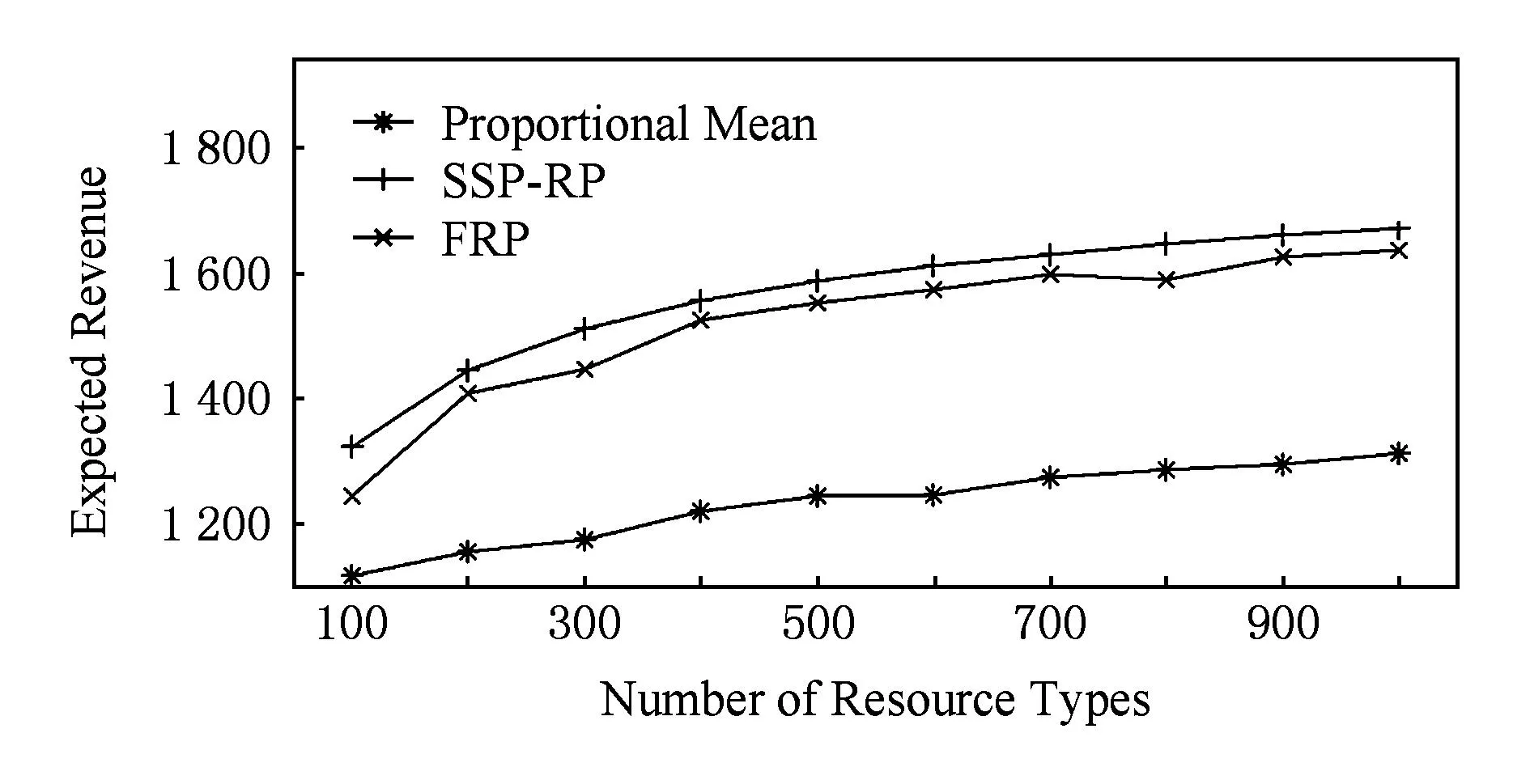
Fig. 3　Expected revenue with different number of resource types under deficit scenario.图3　资源不足时收益与资源数量的关系

Fig. 4　Expected revenue with different number of resource types under surplus scenario.图4　资源盈余时收益与资源数量的关系

同时从图1～4的2个实验中，可看到随着资源数量由不足转为盈余，均值方法的效果也逐渐接近SSP-RP最优求解算法，使得FRP和SSP-RP的优势不明显.分析实验数据后发现，随着资源数量的增加，由于待满足的请求没有变化，问题优化空间缩小导致优化效果不明显.而实际场景中资源数量一般都略有不足，因此FRP相比均值算法仍有很大优势.

我们同时在通用场景中比较了FRP和SSP-RP的效果.首先比较在不同Zipf参数和资源数量I下FRP和SSP-RP期望收益的比率，如图5和图6所示.我们可看到FRP受Zipf参数轻微影响，同时也会受资源总量I的影响，资源不足时资源收益略低一些.分析实验数据后我们发现，因为最后的分配结果会4舍5入到整数，资源不足情况下，舍入对结果影响较大.

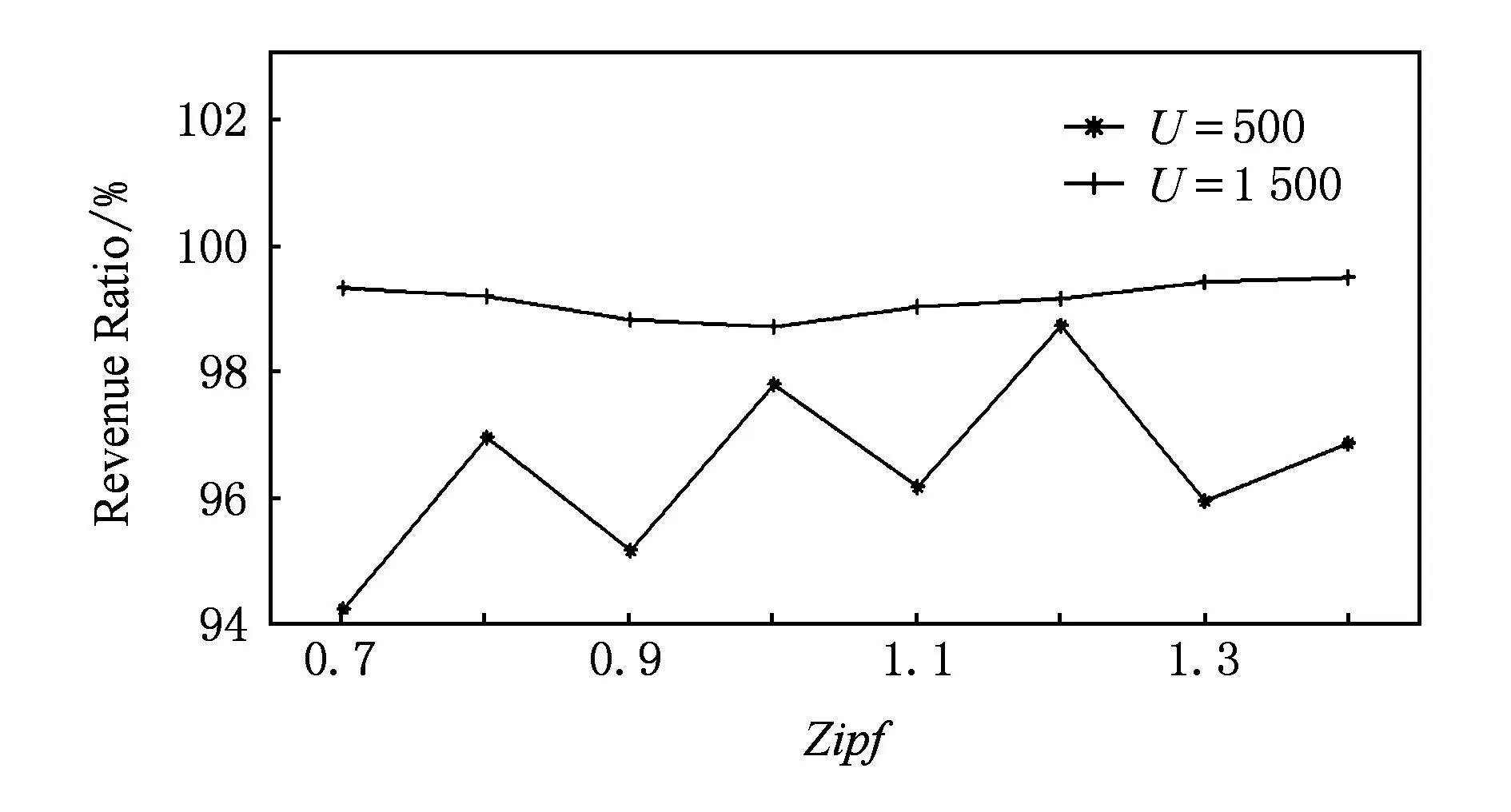
Fig. 5　Revenue ratio of FRP to SSP-RP with different Zipf values.图5　FRP和SSP-RP的收益比率与Zipf的关系

Fig. 6　Revenue ratio of FRP to S-URP with different number of resource types.图6　FRP和SSP-RP的收益比率与资源数量的关系

FRP算法的时间复杂度与精度K成正比，因而我们试比较不同K下FRP的期望收益和SSP-RP算法结果的比值，如图7所示.其中横坐标为FRP求解精度K，取值为10～200；纵坐标为单个K值下不同U时多次实验得到的多个FRP和SSP-RP收益比率的均值.我们可看到，FRP可通过很低的时间复杂度可获得近优解，在所有场景中都能达到SSP-RP的97%以上，且因SSP-RP和FRP的时间复杂度分别为O(IJU)和O(IJK+IKlogK),当λ=10 000且K=10时，FRP能以降低3个数量级的时间复杂度接近最优解99%，具明显的改进效果.

Fig. 7　Average revenue ratio of FURP to SSP-RP with different cycle counts.图7　FRP和SSP-RP的平均收益比率与循环数的关系

4结束语

本文研究了分布式云计算平台中基于随机需求的通用资源分配问题，并提出了可获取近似解的快速求解方法.相比已有文献中的最优解算法，我们的方法可达到最优解的99%，同时计算复杂度只有最优解算法的1‰，是对已有算法的有效补充.

参考文献

[1]YouTube. YouTube homepage[EBOL]. (2005-02-15) [2015-03-12]. http:www.youtube.com

[2]Facebook. Facebook homepage[EBOL]. (2004-02-04) [2015-03-12]. http:www.facebook.com

[3]You Kun, Tang Bin, Qian Zhuzhong, et al. QoS-aware placement of stream processing service[J]. Journal of Supercomputing, 2013, 64(3): 919-941

[4]Qiu Xuanjia, Li Hongxing, Wu Chuan, et al. Dynamic scaling of VoD services into hybrid clouds with cost minimization and QoS guarantee[C]Proc of IEEE Int Packet Video Workshop. Piscataway, NJ: IEEE, 2012: 137-142

[5]Huang Yongfeng, Dong Yongqiang, Zhang Sanfeng, et al. Leftover bandwidth-aware peer selection algorithm for inter-datacenter content distribution[J]. Journal on Communi-cations, 2013, 34(7): 24-33 (in Chinese)(黄永锋, 董永强, 张三峰, 等. 数据中心间空闲带宽感知的内容分发算法[J]. 通信学报,2013, 34(7): 24-33)

[6]Broberg J, Buyya R, Tari Z. Metacdn: Harnessing storage clouds for high performance content delivery[J]. Journal of Network and Computer Applications, 2009, 32(5): 1012-1022

[7]Qiu Xuanjia, Li Hongxing, Wu Chuan, et al. Cost-minimizing dynamic migration of content distribution services into hybrid clouds[C]Proc of INFOCOM 2012. Piscataway, NJ: IEEE, 2012: 2571-2575

[8]Chen Fangfei, Guo Katherine, Lin John, et al. Intra-cloud lightning: Building CDNs in the cloud[C]Proc of IEEE INFOCOM’12. Piscataway, NJ: IEEE, 2012: 433-441

[9]He Zhicong, Gu Guangzhao, Wang Xin, et al. Novel cooperative caching strategies for video streaming distribution based on reconfiguration routers[J]. Journal on Communications, 2012, 33(6): 82-90 (in Chinese)(何智聪, 谷光昭, 王新, 等. 基于可重构路由器上缓存的流媒体协作分发策略[J]. 通信学报, 2012, 33(6): 82-90)

[10]Zhou Jingcai, Zhang Huyan, Zha Wenliang, et al. User-aware resource provision policy for cloud computing[J]. Journal of Computer Research and Development, 2014, 51(5): 1108-1119 (in Chinese)(周景才, 张沪寅, 查文亮, 等. 云计算环境下基于用户行为特征的资源分配策略[J]. 计算机研究与发展, 2014, 51(5): 1108-1119)

[11]Tang Zhuo, Zhu Min, Yang Li, et al. Random Task-oriented user utility optimization model in the cloud environment[J]. Journal of Computer Research and Development, 2014, 51(5): 1120-1128 (in Chinese)(唐卓, 朱敏, 杨黎, 等. 云环境中面向随机任务的用户效用优化模型[J]. 计算机研究与发展, 2014, 51(5): 1120-1128)

[12]Tan B, Massoulie L. Optimal content placement for peer-to-peer video-on-demand systems[C]Proc of IEEE INFOCOM’12. Piscataway, NJ: IEEE, 2012: 694-702

[13]Rochman Y, Levy H, Brosh E. Resource placement and assignment in distributed network topologies[C]Proc of IEEE INFOCOM’13. Piscataway, NJ: IEEE, 2013: 1914-1922

中图法分类号TP301.6

基金项目：国家自然科学基金项目(U1504607,61202099);河南省教育厅科学技术研究重点基金项目(2010A520008,13A413001,14A520018);河南省重点科技攻关基金项目(102102210025);新世纪优秀人才支持计划基金项目(NCET-12-0692);河南工业大学博士基金项目(2012BS011,2013BS003);河南工业大学自然科学基础研究重点培育计划基金项目(2014JCYJ04)

收稿日期：2014-12-08；修回日期：2015-04-08

This work was supported by the National Natural Science Foundation of China (U1504607,61202099), the Key Science and Technology Research Project of Education Department of Henan Province (2010A520008,13A413001,14A520018), Henan Provincial Key Scientific and Technological Plan (102102210025), the Program for New Century Excellent Talents in University of Ministry of Education of China (NCET-12-0692), the Doctor Foundation of Henan University of Technology (2012BS011,2013BS003), and the Plan of Nature Science Fundamental Research in Henan University of Technology (2014JCYJ04).