细长轴磨削时辅助支撑对自由振动的影响

李香飞，苗德华

（天津职业技术师范大学机械工程学院，天津　300222）



细长轴磨削时辅助支撑对自由振动的影响

李香飞，苗德华

（天津职业技术师范大学机械工程学院，天津300222）

摘要：从振动角度分析支撑架刚度对工艺系统的影响，得出细长轴磨削时的受力简化模型。将有支撑架辅助支撑的细长轴简化为中间弹性支撑的超静定梁模型，以支座反力替代弹性支撑的振动系统，根据连续梁的边界条件及弹性支撑处的约束条件，得出频率特征方程和自振频率，将理论推导所得结果与有限元法所得结果进行对比，并分析中间弹性支撑位置变化时，细长轴各阶频率的变化规律。

关键词：细长轴；超静定结构；弹性支撑；磨削加工

轴类零件中长径比大于10及以上的属于细长轴类型。细长轴常用于精密高速传动部件，例如机床、武器装备以及测量仪器等设备。细长轴已加工表面质量是影响这些仪设备使用性能及其自身寿命的主要因素，因此对其进行合理的磨削加工对保证加工质量十分必要。细长轴本身刚度较差，在磨削加工时易产生让刀和振动现象。针对上述现象，国内外学者通过建立加工模型实现在线实时检测与补偿，提高磨削加工质量，这种误差在线补偿技术在行业内获得较好的应用，但对于复杂的工艺模型，该技术还不能满足加工要求。一些学者从磨削参数、磨削液以及安装方式等方面提出了许多新方法，如宋灿等[1]提出以水射流辅助支撑、以射流冲击力抵消背向力的设计思路，获得较好的效果，但该技术还处于试验阶段，不能应用于实际生产中。一般细长轴的加工常采用跟刀架或中心架提高工艺系统的刚度，文献[2]提出采用跟刀架来提高磨削刚度，讨论了跟刀架刚度对系统振动的影响。文献[3]在细长轴磨削工艺改进中提出了在支撑处装加减振棒，提高工艺系统刚度，但没有讨论中心架位置对工艺系统频率的影响。上述文献中都提到中心架支撑托架的固有频率会对工艺系统的振动产生一定影响，因此本文从振动角度研究分析支撑架刚度对工艺系统的影响，得出细长轴磨削时的受力简化模型。根据连续梁的边界条件及弹性支撑处的约束条件，得出频率特征方程和自振频率，同时分析中间弹性支撑位置变化时细长轴各阶频率的变化规律。

1　细长轴加工工艺系统力学模型

采用MM1336外圆磨床进行细长轴加工，为减小固定顶尖支撑力随机变化引起的细长轴振动，采用弹性顶尖的装夹方式，其中一端为液压顶尖，一端为固定顶尖。由于细长轴刚性差，故采用中心架进行辅助支撑。在加工前先对细长轴进行冷校直，采用中心架放在轴中间处的支承方式，使L/d值为原来的1/2，这样在磨削时工艺系统的刚性可增加几倍。在放上中心架之前，须在轴中心架位置处预先磨出一段与支承爪对应的外圆面，其表面粗糙度及圆柱度误差应在公差要求范围内，以免影响加工精度。因此，先磨削中心架位置并留有适当的余量，以减小轴的弯曲变形引起的内应力。

磨削加工时，细长轴会受磨削力Fx、Fy和Fz作用，Fx引起的横向振动可忽略不计。磨削力Fy和Fz引起在xOy平面和xOz平面的横向振动响应分别以y（x，t）和z（x，t）表示，y（x，t）和z（x，t）是关于切削位置x和时间t的二元函数。对于简支梁，其边界条件为：y（0，t）= 0，y（L，t）= 0。中间有中心架辅助支撑的简化模型如图1所示。

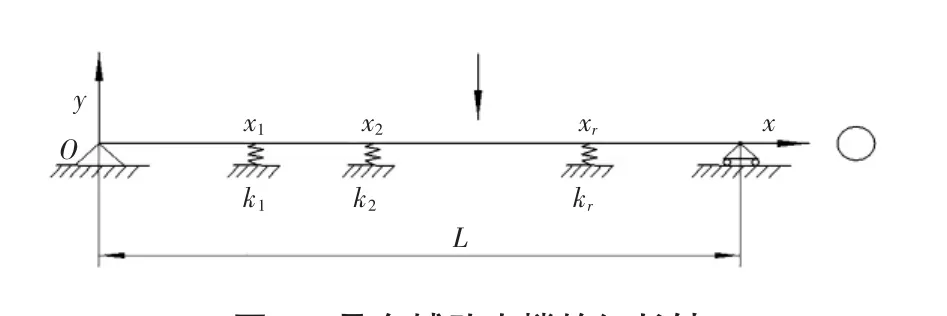
图1　具有辅助支撑的细长轴

将支撑简化为弹性支撑的连续细长轴，其弹性支承的刚度为kr（r = 1，2，…，r）。用集中力代替辅助支撑的简化模型如图2所示[4]。

图2　受力简化模型

激振力为F是切削力（F为不同平面的磨削力Fy、Fz），图2所示的超静定细长轴的强迫振动方程为[4]：

式中：EI为抗弯刚度；ρ为材料密度；A为轴的截面积；f（x，t）为外力，包括弹性支反力和切削力，f（x，t）的表达式为：

式中：v = n·f/60为砂轮沿轴向移动的速度；δ为狄拉克函数；F0为横向力，在xOy平面内F0= Fy，在xOz平面内F0= Fz。

狄拉克函数的特性为：

在Xr处的位移约束条件为：

采用振型分解法对微分方程求解，梁在强迫振动下的动挠度y（x，t）表示为：

式中：φi（x）为主振型函；qi（t）为广义振型坐标，由振型正交性质，对式（4）两边同乘以φn（x）dx并进行积分，得到：

当i≠n时，等式右边积分为0，于是得到第n项的振型表达式为：

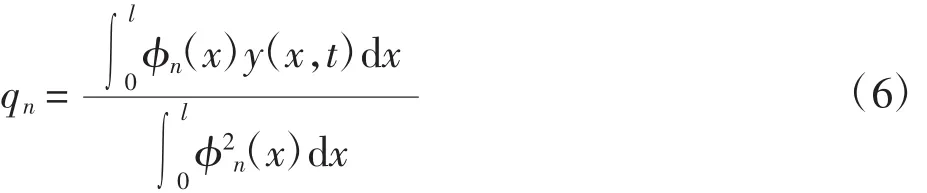
对简支梁的振动方程进行分解，将式（2）—式（4）代入式（1）得：

将式（3）代入式（1）化简后，两端同乘以φn（x）dx，再进行全长积分，得到第n个振型的广义坐标运动方程为：

式中：对于等截面的简支梁，振型函数设为三角函数：

将式（9）代入式（8）得：

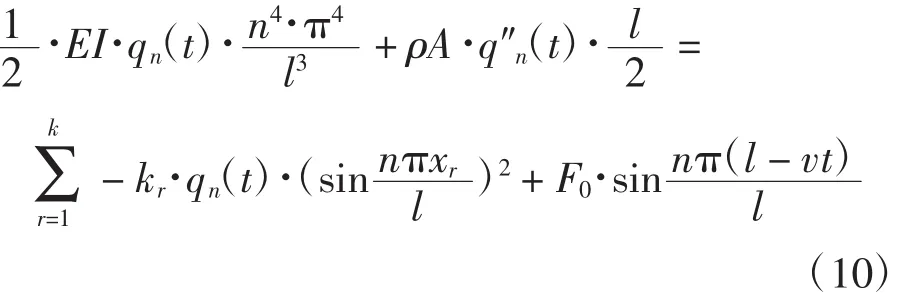
令

则式（10）化简为：

由于磨削时，先磨削弹性支撑位置，并留有较小的余量，因此初始时刻，细长轴的弯曲挠度忽略不计。在t = 0时刻，qn（0）= q′n（0）= 0。令τn= nπv/l

可得：

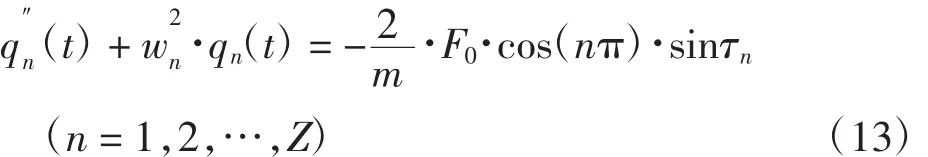
方程（13）的通解为：

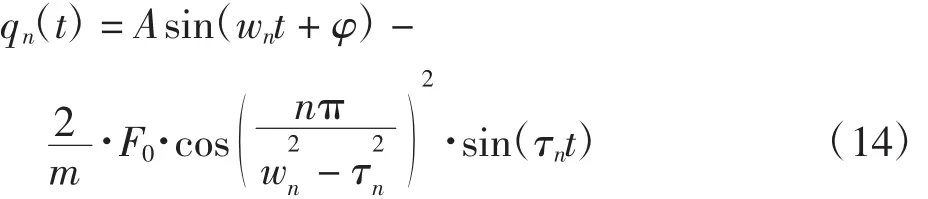
由初始条件qn（0）= q′n（0）= 0可得：

将式（9）、式（14）和式（15）代入式（4）中，求得由移动切削力引起的xOy平面内工艺系统位移响应为：

由于xOz平面内的受力与xOy平面内相同，根据以上方法可得到xOz平面内F0引起的轴的振动响应。

2　实例分析

一中心架支撑简图如图3所示。图中两端为简支的两跨连续梁，梁的横截面尺寸为b×h = 0.2×0.3 m，单段长度为L1= L2= 3 m，材料密度为ρ=7 800 kg·m-3，弹性模量为E = 210 GPa，弹性支撑刚度为K = 5.426× 107N/m。

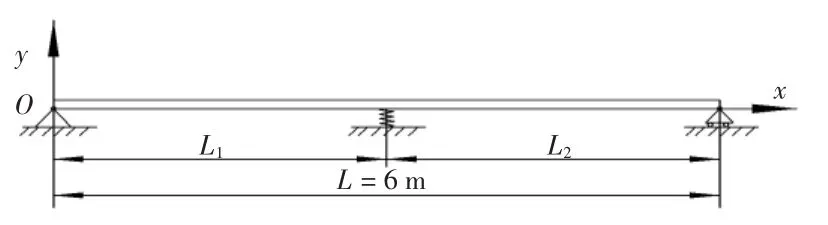
图3　一中心架支撑简图

在没有施加切削力时，低阶频率对系统影响最大，因此取前3阶频率。系统的频率由式（11）计算得到，其结果与文献[4]得到的结果进行比较，如表1所示。采用本文的公式得到的结果与有限元分析得到的结果相比，二者误差小于1%，结果基本一致，由此验证了本文推导过程的正确性。

表1　本文计算的前3阶频率结果与有限元法计算结果的比较

3　支撑位置对频率的影响

现针对两中心架支撑的工艺系统进行分析，中心架位置如图4所示。

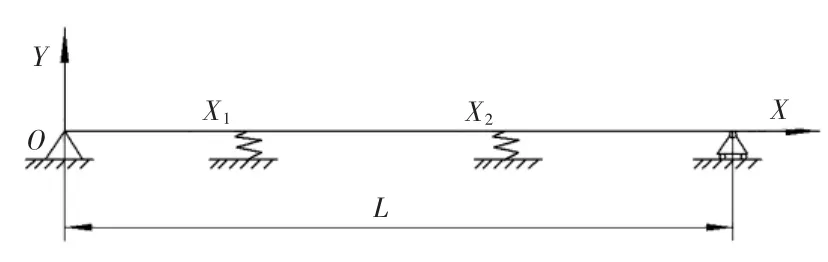
图4　中心架位置简图

由图4可知，X1、X2的边界条件为：

将式（17）代入式（11）化简得：

令

对式（19）求关于X1、X2的偏导数，获得使βn最大值时X1、X2的取值，X1、X2的取值情况如表2所示。

由表2可知，当X1、X2对称布置时，βn达到最大值。设ε是X1与l的比值，X1、X2呈对称布置，由式（17）可知ε取值范围是[0，1/2]，采用Matlab绘出1～3阶频率与中心架位置的关系曲线，如图5所示。

表2　最大值时X1、X2的取值情况

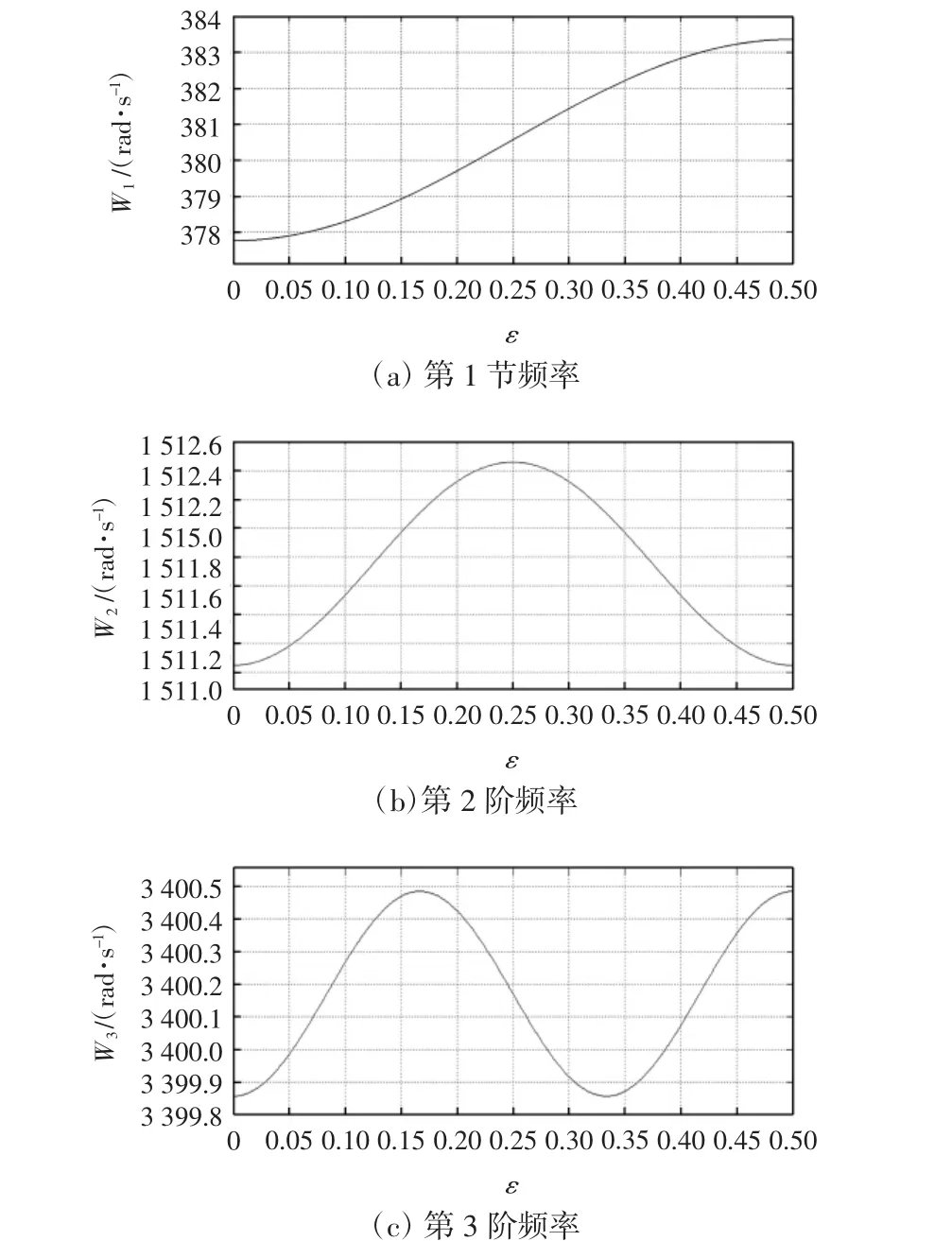
图5　1～3阶频率与中心架位置关系曲线图

由表2数据可知，采用对式（19）求偏导获取最优中心架位置的方法可行，通过数据分析得出两中心架对称布置时，式（19）取得最大值。由图5(a）可知，系统第1阶段频率随中心架位置的变动而变动，变化规律呈抛物线状，当中心架在细长轴1/2处，系统的频率取得最大值；由图5（b）可知，系统第2阶段频率变化规律与图5（a）的一致，但峰值位置发生变化，出现在细长轴1/4处；由图5（c）可知，第3阶频率与支撑位置之间的关系呈正弦曲线，在细长轴1/6处系统频率达到峰值，这与实际加工时支撑布置工况相符合。通过对研究所得数据进行分析，从理论上解释了中心架对称分布的合理性。由分析可知，在第1阶频率，两中心架在轴的中间位置重合，此处为刚性最薄弱的环节；在第2阶频率，刚性薄弱环节在轴的1/4处与3/4处；而第3阶频率的刚性薄弱环节在轴的1/6处与5/6处。

4　结束语

本文研究了细长轴磨削时弯曲变形及振幅等对磨削的影响。基于横向振动原理建立了细长轴磨削过程的振动模型，并从力学及数值分析方面得出辅助支撑部件刚度引起的被加工工件振动响应的关系式；通过数值计算以及仿真分析了中心架尺寸变化对工艺系统振动频率的影响，找到了中心架布置的最佳位置；从理论角度提出可通过中心架对称布置来提高工艺系统刚度，减小加工变形。本研究的结果为细长轴类磨削工艺制定提供了理论依据。

参考文献：

［1］宋灿，吕彦明，徐看，等．水射流辅助支撑改善细长轴加工中的弯曲变形［J］．机械设计与研究，2015，31（1）：99-101.

［2］孙伏，严长明．细长轴磨削加工过程有限元分析［J］．陕西理工学院学报：自然科学版，2015，31（4）：9-11.

［3］董华超，李智勇．不锈钢细长轴磨削加工的工艺改进［J］．精密制造与白动化，2012（2）：51-53.

［4］张鹏，叶茂，徐梅玲，等．基于反力替代的弹性支撑连续梁桥自由振动［J］．广州大学学报：自然科学版，2013，12（6）：37-40.

［5］潘德军，张家库.高速电主轴系统固有频率与临界转速分析［J］．轴承，2008（10）：24-27.

［6］韩贤国，王敏杰，欧阳华江．车削过程中工件的振动力学建模与分析［J］.机械强度，2012，34（5）：644-649.

［7］马生彪．磨削加工过程振动仿真与磨削温度预测［D］．郑州：郑州大学，2011．

［8］吕长飞，李郝林．外圆纵向磨削力和磨削功率模型研究［J］．现代制造工程，2011（12）：72-75．

［9］陈涛，周全华．细长轴的磨削工艺分析［J］．机械工程师，2014（8）:228-229.

［10］傅玉灿，田霖，徐九华，等．磨削过程建模与仿真研究现状［J］．机械工程学报，2015，5（7）：197-203.

Effects of assistant supporting mechanism on free vibration in slender bar grinding

LI Xiang-fei，MIAO De-hua
（School of Mechanical Engineering，Tianjin University of Technology and Education，Tianjin 300222，China）

Abstract：Study on the influence of brace stiffness on the process system from a perspective of vibration analysis and obtains a simplified mechanical model of slender shaft grinding.The slender bar with center rests is simplified to a static indeterminate beam with flexible supports.According to the boundary conditions of continuous beam and elastic constraints，the frequency equation and the natural frequencies are obtained.The results from this theoretical research and the finite element method are compared.Furthermore，this paper obtains the patterns of each order natural frequency by analyzing the change of elastic support location.

Key words：slender bar；statically indeterminate structure；flexible support；grinding machining

作者简介：李香飞（1986—），男，硕士研究生；苗德华（1957—），男，教授，硕士生导师，研究方向为机械设计、新材料的开发与性能等.

基金项目：天津市科技计划项目（15ZXZNGX00220）.

收稿日期：2016-01-07

中图分类号：TG580

文献标识码：A

文章编号：2095－0926（2016）01－0041－04