大学生数学焦虑因素的显著关联水平及聚类分析*

范大付

百色学院教务处，广西　百色　533000



大学生数学焦虑因素的显著关联水平及聚类分析*

范大付**

百色学院教务处，广西百色533000

摘要：通过对大学生数学焦虑因素的非参数统计分析与研究，统计出数学焦虑的显著程度、关联特征水平及聚类分析相关结果。

关键词：非参数；数学焦虑；关联水平；聚类分析

大学生数学焦虑是一种过分焦虑大学数学而影响数学学习效率的一种消极认知、悲观厌学的数学学习行为表现及心理体验。而非参数统计是一种不依赖于总体分布和不涉及总体参数的检验方法。其原理：就是在原假设下的条件下，根据观测值的相对大小建立相应的检验统计量，并确定其的分布，然后判断这些统计量的数据是否在原假设下是否为小概率事件[1]。本文以百色学院学生为研究对象，收集到09级数学与应用数学本科有效问卷85份、09级物本有效问卷31份 。本文以spss统计软件作为研究工具对数学焦虑进行非参数统计分析研究

一、数学焦虑各因素显著水平及程度

据教育生理学相关研究表明，大学生数学焦虑因素主要有下列五种：数学专业与非数学专业(即专业差别)、性别差异、课堂提问方式、学习障碍、考核方式。为了科学分析这五种焦虑因素的焦虑水平，我们对文[2]中各焦虑量数据换算成相应得分后编制成表1-1。

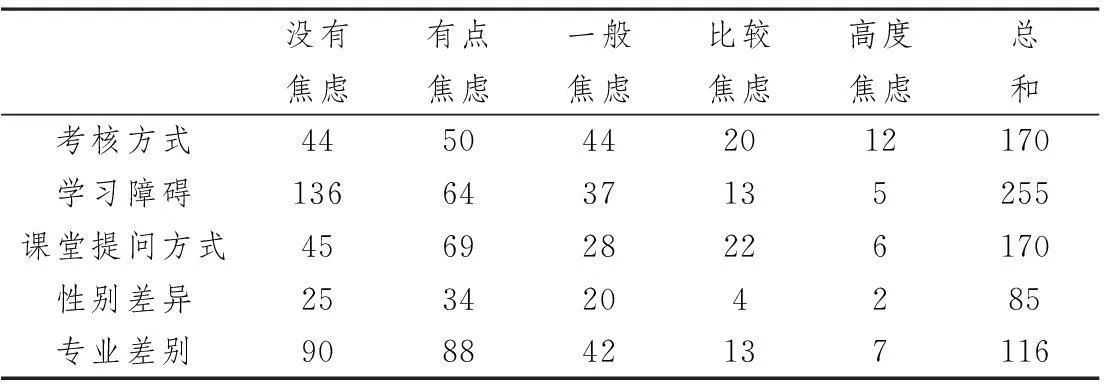
表1-1　数学焦虑因素焦虑量统计数据表

把上表数据输入软件，得各因素焦虑水平，如表1-2：

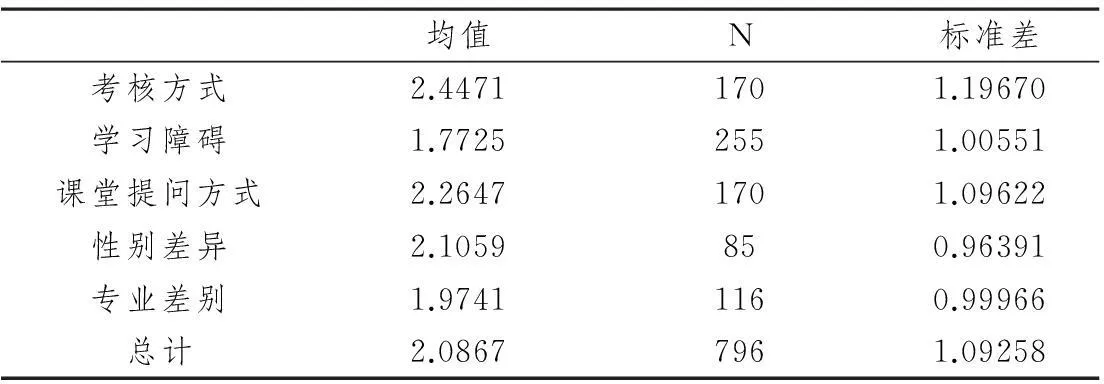
表1-2　数学焦虑量统计分析表

从表1-2可知，五种数学焦虑因素水平依次为：考核方式>课堂提问方式>性别差异>专业差别>学习障碍。可见，焦虑量最大的为考核方式，焦虑量最小的为学习障碍，五种焦虑因素量的波动性几乎相等，近似等于1，易知五种焦虑因素的调查统计数据比较科学。而五种因素的显著程度在文[2-3]中已统计出结果，即闭卷显著于开卷、口头提问方式显著于书面提问方式、学习障碍不问时产生的数学焦虑显著于问老师、问同学两种方式、女性显著于男性、数学专业显著于非数学专业，本文不再讨论。

二、数学焦虑产生因素的数据的分布及数据属性特征

调查数据的分布特征及属性在概率统计分析中有着比较重要的作用地位。一是，可以分析大学数学焦虑因素的数据分布特征。二是，可以了解数学焦虑因素的数据关联属性。三是，为解决数学焦虑提供科学的信息来源及应对策略。

(一)数学焦虑产生因素的数据分布特征

为了了解数学焦虑产生因素的数学焦虑量数据的未知分布，我们主要采用 拟合优度检验。下面我们就用 检验来分析这五种因素的分布情况。先统计好数学焦虑量频率数据，如下表2-1。

表2-1　数学焦虑因素的焦虑量频率表 [3]

对于给定的显著水平α=0.05，在spss中输入上表数据，经过K-S统计分析后，获得数学焦虑相关分布特征统计结果，如表2-2。

根据表2-2的分布特征统计结果数据可知，五种焦虑因素的正态分布、均匀分布、指数分布的检测显著性概率约等于0.000，都小于0.05，可见五种数学焦虑因素的统计数据均不服从正态、均匀、指数三种分布。而考核方式、性别差异的泊松分布的显著性概率分别为0.157、0.161，都大于0.05，即考核方式、性别差异服从泊松分布。专业差别、课堂提问方式、学习障碍三个因素的泊松分布的显著性概率均小于0.05，即不服从泊松分布。从表2-2统计分析结果可知，五种数学焦虑因素中，唯有数学考核方式、性别差异两个因素服从泊松分布。[4-6]

表2-2　数学焦虑因素的分布特征统计结果表

(二)数学焦虑因素的数据属性特征

在数学焦虑因素的数据属性特征的非参数统计分析中，不仅要分析数据的属性特征，并了解多变量不同取值下的分布，而且还要分析掌握多变量的联合分布特征，以此分析变量之间的相互影响及水平关系。

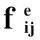
表2-3　数学焦虑各产生因素的焦虑量数据理论频数

对于给定的α=0.05，根据Pearson χ2检验原理，输入表2-3数据，卡方检验结果如表2-4：

表2-4　卡方检验

a.2单元格(8.0%)的期望计数少于5.最小期望计数为2.99。

对于定的显著水平α=0.05，根据表2-4统计结果Pearson χ20=70.991，相伴概率为0.000，则有相伴概率小于0.05，易知卡方检验显著，焦虑程度与焦虑类型之间几乎没有关联性。

表2-5　对称度量数据

根据表2-5分析结果易知，关联水平GL=0.286，则可判断出数学焦虑因素与焦虑程度的关联性非常小，每个焦虑因素的焦虑量几乎没有关联，即相互独立。

(三)数学焦虑产生因素的数据的聚类分析

聚类分析是将样本个体或指标变量按其具有的特性进行分类的一种统计分析方法，其原理是选择相关的观测指标，通过不同的距离实现分组，使组内的数据对象具有高度的相似度[11]。现根据表1-1数据，将变量分成三类，利用spss进行K-均值聚类分析，得到表3-1 最终聚类中心、表3-2 最终聚类中心间的距离、表3-3 聚类成员分析结果：

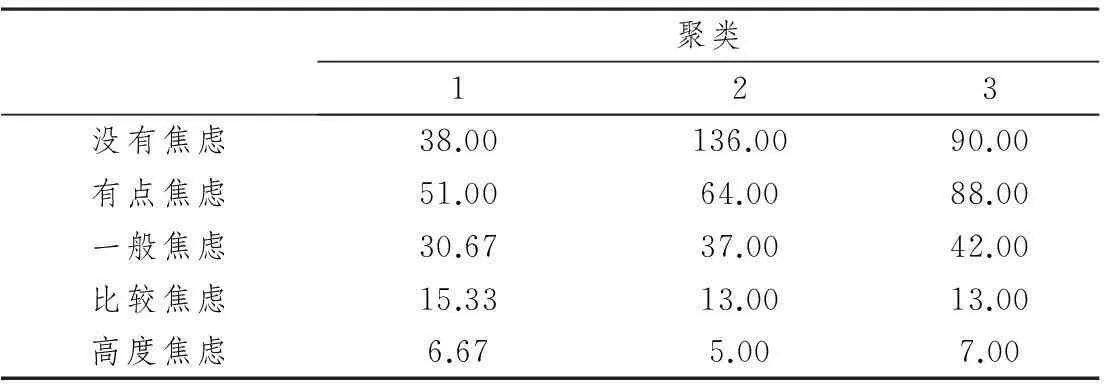
表3-1　最终聚类中心

表3-2　最终聚类中心间的距离

表3-3　聚类成员

通过聚类分析的结果可以看出，五种焦虑类型若分成3类的话，数学考核、数学课堂提问方式、性别差异这三楼比较相似，距离也远，焦虑程度也高。因此，我们在解决数学焦虑问题时，可考虑主要从这三个方面下手。

[参考文献]

[1]谷彬，赵彦云.非参数统计作用与发展[J].中国统计，2004，38(4)：56-57.

[2]范大付.大学生数学焦虑产生因素的非参数统计分析[J].重庆理工大学报(自然科学)，2012，26(7)：94-99.

[3]范大付.非参数统计在大学生数学焦虑中的应用研究[M].南宁：广西大学，2012.

[4]朱新玲，黎鹏.非参数检验在市场假查中的应用[J].江苏统计应用研究，2003，19(11)：24-25.

[5]徐明.两种非参数统计方法的应用[J].体育科学，1997，15(6)：88-89.

[6]洪楠.SPSS for Windows统计分析教程[M].北京：电子工业出版社，2000.

[7]易丹辉等.非参数统计：方法与应用[M].北京：中国统计出版社，2009.

[8]孙山泽.非参数统计讲义[M].北京：北京大学出版社，2000.

[9]王静龙，梁小筠.非参数统计分析[M].北京：高等教育出版设，2006.

[10]范金城，梅长林.数据分析[M].北京：科学出版社，2002.

[11]刘震，吴广等.统计分析与应用[M].北京：电子工业出版社，2011.

Significant correlation level and cluster analysis of College Students' mathematics anxiety

FAN Da-fu

Office of academic affairs，Baise University，Baise，Guangxi 533000

Abstract：by non parametric statistical analysis and Research on the factors of College Students' math anxiety，analysis of related results feature level and clustering correlation significant degree of math anxiety and statistics.

中图分类号：O1-4

文献标识码：A

文章编号：1006-0049-(2016)02-0007-02

**作者简介：范大付(1974-)，男，广西灌阳人，硕士，讲师，广西百色学院教务处，研究方向：应用数学、基础数学。

*广西高校科学技术研究项目(2013LX146)；广西高校科学技术研究项目(YB2014390)；广西自然科学基金(2014GXNSFAA118030)；广西高等教育本科教学改革工程项目(2015JGZ160)；广西高等教育本科教学改革工程项目(2015JGB376)。