基于虚拟脱靶量预测的准闭环校射方法

吴映锋，李文才，王长城

（1.解放军63961部队，北京　100012；2.中国兵器工业第五八研究所，四川　绵阳　621000）



基于虚拟脱靶量预测的准闭环校射方法

吴映锋，李文才，王长城

（1.解放军63961部队，北京100012；2.中国兵器工业第五八研究所，四川绵阳621000）

摘要：针对传统高炮大闭环校射脱靶量不易检测、可校射时间短暂，提出了一种基于虚拟脱靶量预测的准闭环校射方法。首先给出了弹丸双站角度测量的初始状态估计算法；其次，结合外弹道理论建立了一种虚拟等距脱靶量的预测模型，分析了射击校正量的估计方法与准闭环校射方案的实现流程。该方法避免了大闭环校射对脱靶量的直接检测，并提高了高炮闭环校射的时效性。

关键词：高炮，火控，虚拟脱靶量，准闭环校射

0　引言

高炮作为末端防御的最后一道屏障，在拦截快速近程或复杂环境下的低空目标中具有不可替代的优势［1］。随着尖端军事技术在空袭作战中的应用，空袭兵器多样化、作战手段复杂多变，使高炮武器系统面临着日益严峻的形势，促使其向智能化、网络化与高精度方向发展［2-3］。大闭环校射作为改善高炮射击精度的一种重要途径，自被提出以来便成为高炮火控系统研究领域经久不衰的热点问题之一［4-7］。

大闭环校射基于对脱靶量的实时测量，通过对射击过程的反馈控制，实现对射击误差在线修正。脱靶量检测与校射实时性是制约大闭环校射工程化应用的关键问题。由于弹丸体积小，远距离特征不明显，难以检测、捕捉与跟踪；当其接近目标时，观测易受干扰，给弹丸、目标的分辨带来困难，造成脱靶量不易准确检测；其次，大闭环校射中只有在弹丸飞抵目标时才能测到脱靶量，即在首发弹整个飞行时间内的射击为开环的，不可校射，而高炮射击过程原本短暂，可实施大闭环校射的时间也就更为短暂［8］。为此，本文针对大闭环校射存在脱靶量不易检测、校射时效性不足，提出了一种基于虚拟脱靶量预测的准闭环校射方法。通过对弹丸初始轨迹的测量跟踪，结合外弹道学原理，分析了虚拟等距脱靶量的预测模型，并给出了射击校正量的估计方法与方案实现流程。

1　问题描述

图1　基于虚拟脱靶量预测的准闭环校射原理示意

基于虚拟脱靶量预测的准闭环校射基本原理如图1所示。探测设备在跟踪被拦截目标的同时，利用两部空间分布式布局的光电跟踪仪，对已发射弹丸的初始阶段运动轨迹进行实时采集与跟踪，以确定其初始段运动状态，基于外弹道模型积分推算观测过程终止之后的弹道轨迹。结合目标跟踪装置输出的目标航迹信息，实时预测本次射击的虚拟脱靶量，经闭环校射软件实时处理，求出待发射弹丸的射击修正量，修正射击诸元，实现在线校射的闭环火力控制。

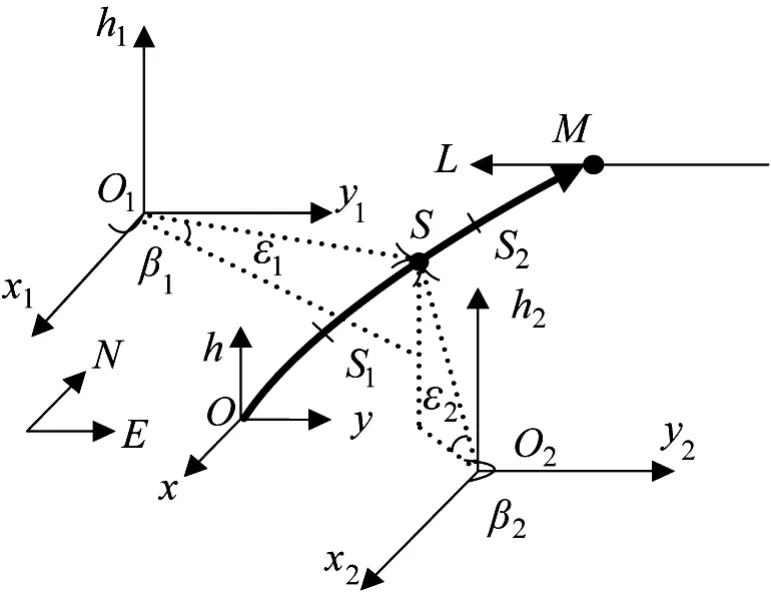
图2　准闭环校射系统空间几何关系

光电跟踪仪、火炮空间布局示意与坐标系定义如图2所示。其中，O为高炮大地坐标原点，正东为x轴正向，正北为y轴正向，xyh遵守右手定则。L表示目标航路，M为理论未来点，OM为弹丸飞行轨迹。O1、O2分别是光电跟踪仪坐标原点，坐标轴指向与高炮大地坐标轴相同。S1，S2为一射击中弹道观测段，（xb，k，yb，k，hb，k）表示k时刻弹丸在Oxyh中的位置坐标（弹道S点），光电跟踪仪通过实时跟踪、采集弹丸视频图像，经图像处理，提取弹丸质心在本地坐标系下的俯仰角εi，k、方位角βi，k测量：

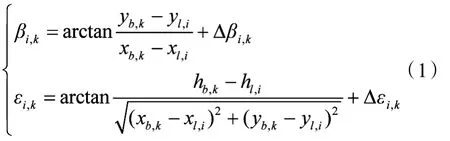
其中i=1，2，将上式改写成向量形式：

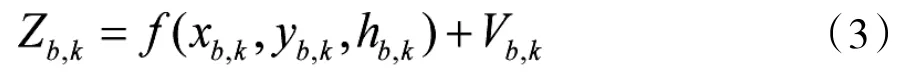
其中f（xb，k，yb，k，hb，k）表示直角坐标到角度的非线性变换函数，Vb，k是均值为0，协方差为Rb，k服从高斯分布的测角误差向量

2弹丸初始段状态估计

记弹丸k时刻状态量为Xb，k，Xb，k=［xb，k，yb，k，hb，采用考虑重力加速度的Singer模型描述弹丸初始段轨迹运动状态：

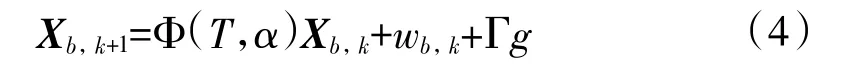
其中Φ（T，α）=ΦS（T，α）⊗I3，ΦS（T，α）为Singer模型的状态转移矩阵，是采样周期T与机动频率α的函数，⊗表示矩阵Kronecker乘积。wb，k为利零均值的高斯噪声向量，协方差为Q（T，α，σ2m）=QS（T，α，为Singer模型的过程噪声协方差，σ2m为加速度方差。Γ=［01×8，-1］T，g为重力加速度。通过基线标定，可确定两个观测站的空间位置坐标，只要得到弹丸相对观测站的方位角与俯仰角，根据空间观测射线相交原理，可确定其位置坐标，即状态可观测。由式（1），观测模型为非线性方程，要确定弹丸的初始阶段运动状态即需解决非线性滤波问题，本文采用UKF滤波，步骤如下：

Step 1.初始化状态X^b，0，方差Pb，0

Step 2.计算X^b，ksigma点Xi，k及相应的权值：

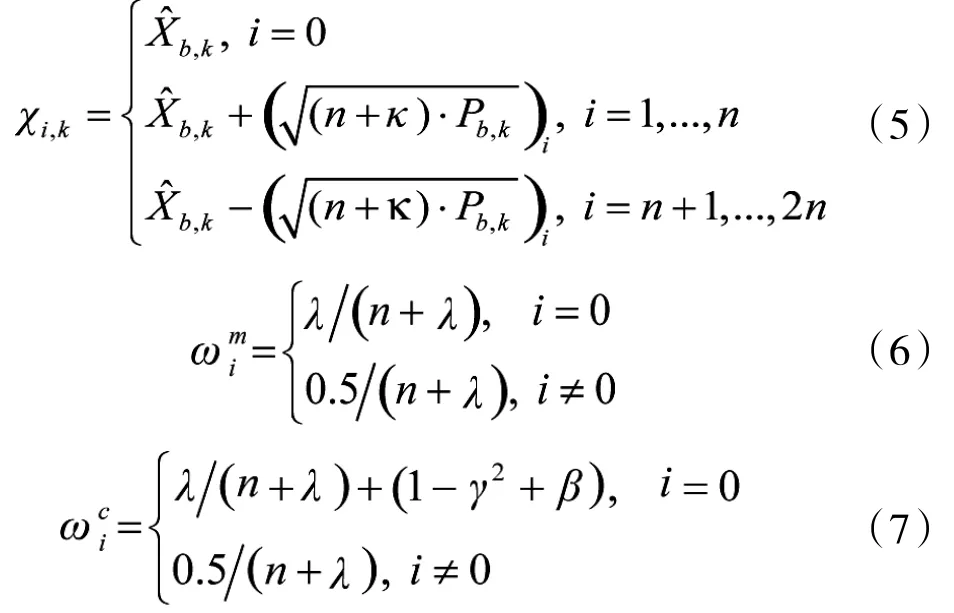
Step 3.预测：

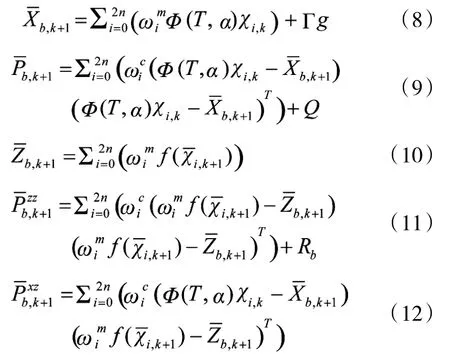
Step 4.更新：

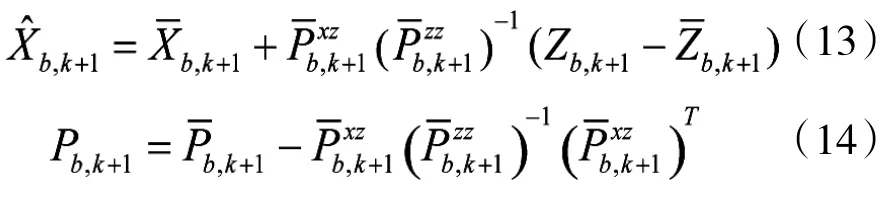
由于观测站呈空间分布式布局，观测站之间数据传输存在延迟，且各站观测采样周期、数据处理能力存在差异，在利用角度数据估计弹丸运动状态之前，需对观测站数据预处理，主要包括时空误差配准、野值剔除等环节。解决数据的空间配准，一般可采用基线测量、寻北定向等标定手段确定观测站在高炮坐标系中的位置{xi，l，yi，l，hi，l}i=1，2及其本地坐标系{Oixiyihi}i=1，2坐标轴指向，根据式（1）将弹丸观测站角度测量转换为在Oxyh中的坐标表示。针对数据的时间配准，可利用目标数据携带的时标与时统信号，采用虚拟融合法或内插外推法，将双站测角数据校准到固定的数据处理周期。

3基于虚拟脱靶量的准闭环校射

3.1弹丸飞行轨迹预测

基于上述数据处理方法，通过两部光电跟踪仪对弹丸的短时连续观测跟踪，便可确定弹丸的运动状态xb，k。针对某一次连续观测，记弹丸出膛瞬间的时刻为t0，结束对弹丸跟踪的时刻为te，在te时刻，以弹丸质心O'为原点固定设置坐标系O'x'y'h'，其定义为：记通过弹丸合速度方向且与大地垂直的平面为A'，通过弹丸质心O'且与高炮坐标系中Oxy平行的平面为B'，A'与B'的交线为x'轴，其与合速度方向夹角小于90°的方向为正，过O'点垂直地面、方向向上为h'，x'y'h'符合右手定则，如图3所示。记（xb'yb'hb'）为弹丸在O'x'y'h'中的位置坐标，v为切向速度，θ为方向倾角，不考虑横风、偏流等因素的影响，可得到简单的外弹道方程［9］：为弹道系数，p为气压，ρon、ρ为标准空气密度和空气密度，τ为虚温，τon为标准地面虚温，Cxon为阻力系数，g为重力加速度，R1为气体常数，Cs为音速，k为空气比热比。本文中针对的是己方发射的弹丸，系数c为已知量，在简化条件下若能确定初始状态θ（te），v（te），便可在观测跟踪后预测弹丸运动状态。记te时刻在高炮坐标系中，由UKF滤波得到的弹丸位置、速度量为：xb则

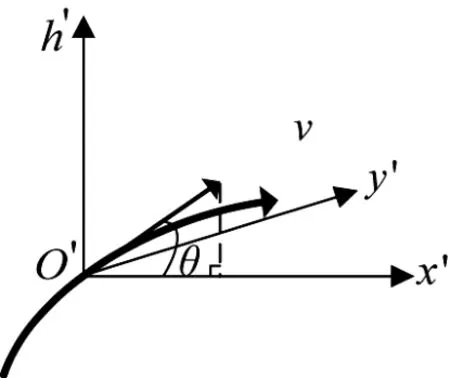
图3　弹道预测坐标系

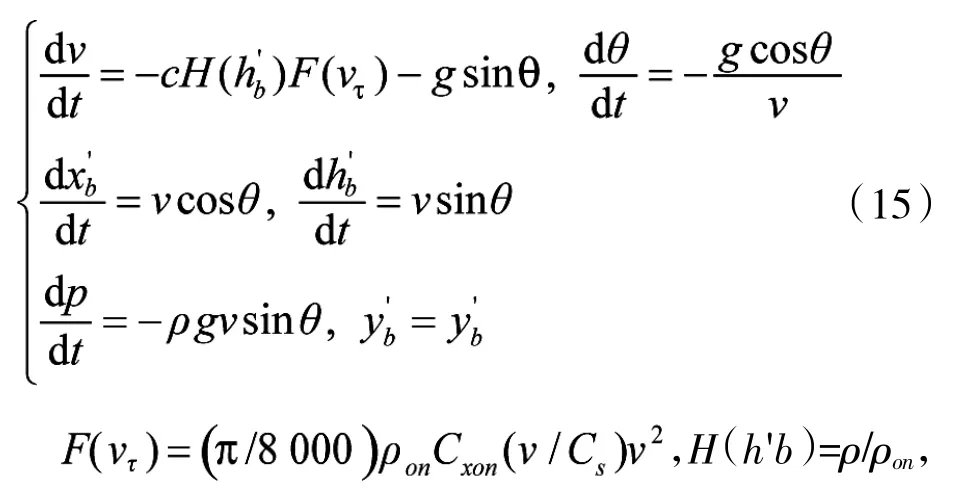
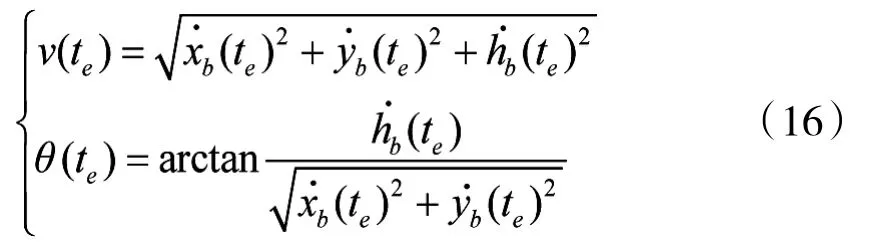
3.2虚拟等距脱靶量预测与校射

根据式（16）确定的初始条件与式（15）的弹道微分方程，利用弹道积分，可预测以te为初始时刻，间隔时间Tf-te+t0后的弹丸状态。利用UKF得到的弹丸运动估计量是在高炮坐标系Oxyh中表示的，而通过弹道积分获得的弹丸预测坐标在其预测坐标系中表示。由图3可知，坐标系O'x'y'h'可看做高炮坐标系分别沿Ox、Oy与Oh平移Δx、Δy与Δh后，再绕Oh逆时针旋转φ得到：

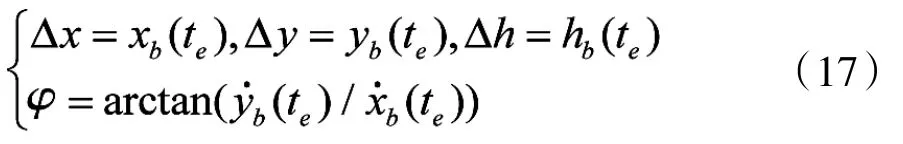
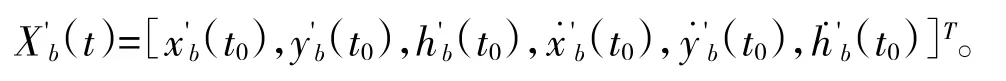
记t时刻在坐标系O'x'y'h'中的弹道预测量为据式（17）所示坐标变换参数，可得到弹道预测状态在高炮坐标系中的表示Xb（t）：

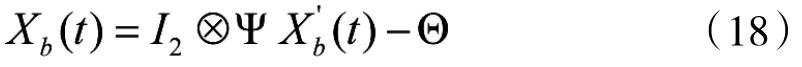
其中

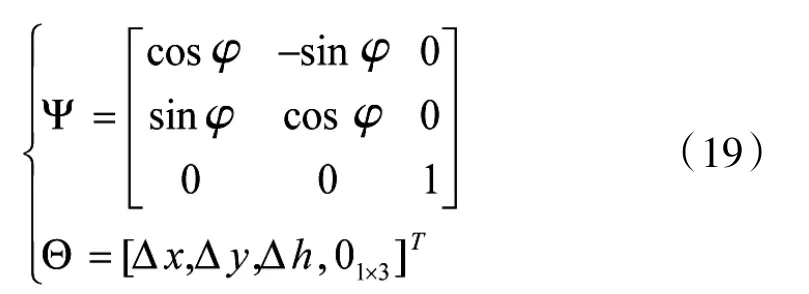
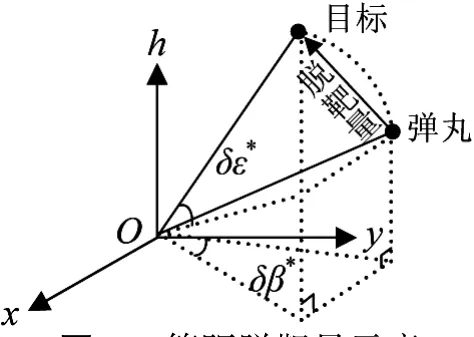
图4　等距脱靶量示意

严格意义上的脱靶量是指目标航迹与弹丸轨迹间的最短距离矢量。由于该定义不利于实际量测和处理，一般采用便于数学处理的等距脱靶量，即目标与弹丸相对运动过程中，两者与高炮距离相等时的距离矢量，本文以弹目俯仰、方位角之差δε*，δβ*表示，如图4所示。联合目标航迹预测与弹道积分方程，利用插值方式，可得到弹丸、目标与高炮距离相等的时间点，将此时的俯仰角、方位角偏差视为脱靶量。

在大闭环校射中，为了确立虚拟脱靶量与发射时刻的对应关系，需对其建模。一般可将其分解为系统误差、相关随机性误差和不相关随机误差3部分［9］，以俯仰角偏差δε*k为例：

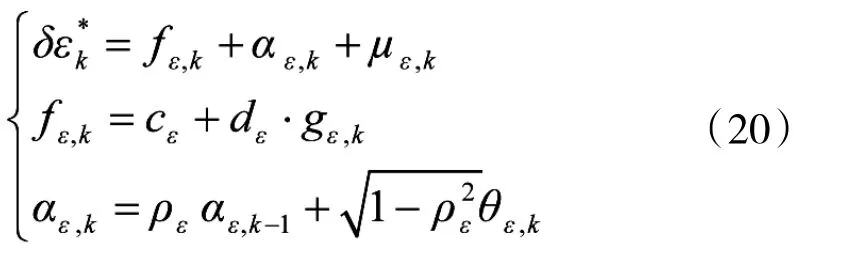
其中，cε与dε为常值误差，gε，k与gβ，k为已知的距离确定性函数。αε，k为宽平稳一阶马尔可夫过程，ρε为相关系数，με，k与θε，k均为零均值的高斯白噪声。得到虚拟脱靶量序列后，应用Kalman滤波等估计方法可得到αε，k、cε与dε的估计值α^ε，k、c^ε与d^ε，相应的最佳校正量Uε，k为：

综上，给出基于虚拟脱靶量的准闭环校射流程，见图5所示。

4仿真分析

经上述分析，本文校射方法较大闭环校射的本质区别在于脱靶量的获取方式不同。根据虚拟脱靶量准闭环校射的实现流程，脱靶量的关键在于对弹道初始段运动参数估计与弹道预测精度。考虑到实验条件限制，本文仅对初始段弹丸跟踪精度与弹道预测精度进行仿真分析。

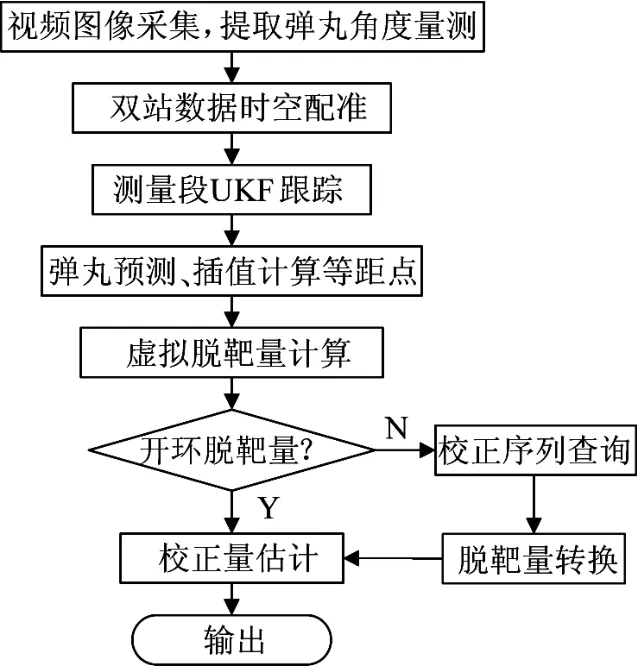
图5　基于虚拟脱靶量的准闭环校射流程

图6　光电跟踪仪布站示意图

考虑如图6所示的一字（a）、三角（b）两种典型的布站方式。弹丸初速为848.53 m/s，方向矢量在Oxy平面内的投影沿x轴正向并与其平行，方向倾角45°，布阵中基线分别为l1=100 m，l2=100 m，弹道跟踪测量段为100 m≤h≤800 m。光电跟踪仪测角标准差分别设定为0.5 mil，0.8 mil，1.2 mil。利用蒙特卡洛仿真，结果如图7～下页图10所示。

图7　一字布阵弹道初始段跟踪误差（方位角）

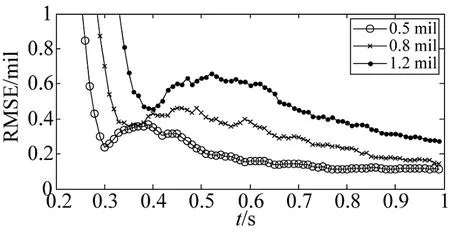
图8　一字布阵弹道初始段跟踪误差（俯仰角）

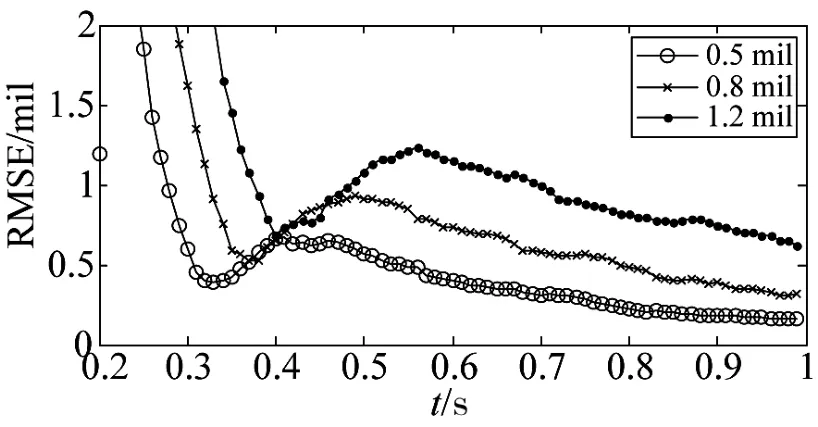
图9　三角布阵弹道初始段跟踪误差（方位角）

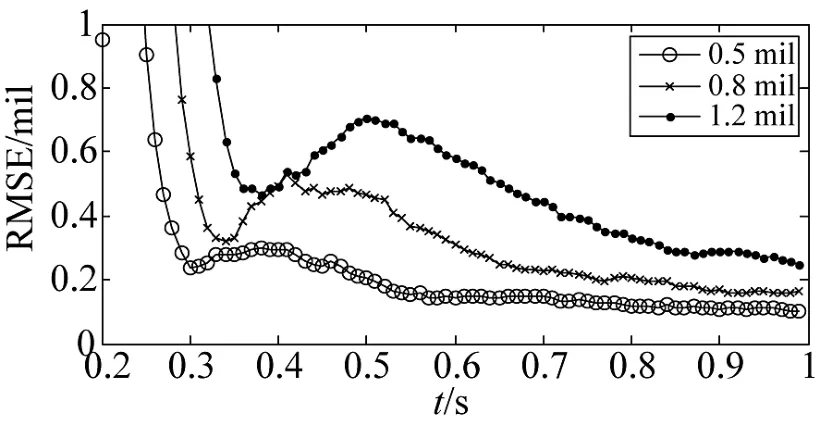
图10　三角布阵弹道初始段跟踪误差（俯仰角）

可见，初始段弹道跟踪误差受布站方式与光电跟踪仪角度误差的影响，表1为t=0.8 s的跟踪误差统计结果。经比较，布站方式对俯仰角跟踪精度影响较小，而采用一字布站方位角跟踪精度明显优于三角布站方式。根据仿真结果，采用一字布阵，若光电跟踪仪测角误差控制在1 mil左右，在100 m≤h≤800 m的初始段弹道中，方位、俯仰跟踪均方根误差（RMSE）分别在0.2 mil～0.3 mil、0.3 mil～0.6 mil范围内，可满足火控系统精度要求。

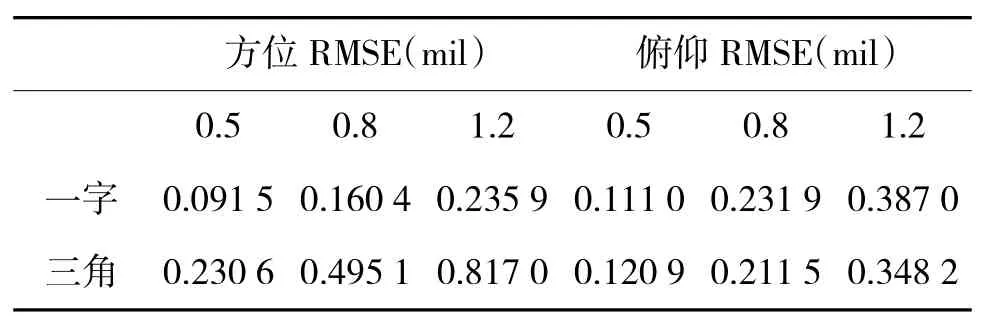
表1　t=0.8 s跟踪误差RMSE

5　结论

本文提出了一种基于虚拟脱靶量预测的准闭环校射方法，通过对弹道初始段轨迹的观测跟踪，结合外弹道积分与目标航迹信息，推导了虚拟等距脱靶量的预测模型，并分析了射击校正量的估计算法。与传统大闭环校射方法相比，克服了脱靶量难以检测的不足，更加有利于工程实现；其次，基于弹道预测方式的校射方法，在弹丸未到达理论未来点之前便可确定待发射弹丸的射击修正量，为高炮拦截争取了更加充裕的时间实施火力闭环控制，提高了在线校射的时效性。同时，本文在弹丸轨迹预测过程中采用了外弹道简化模型，不可避免地引入了弹道预测误差，如何提高弹丸轨迹预测精度进而为后续校射提供更为准确的脱靶量信息，仍需进一步研究。此外，鉴于实验条件的限制，本文仅从理论方面分析了所提方法的系统构成、虚拟脱靶量预测模型和校射原理，对该方法校射性能的实验验证有待进一步探索。

参考文献：

［1］薄煜明，郭治，杜国平，等.高炮与防空导弹在近程防空反导中的互补性［J］.兵工学报，2002，23（3）：164-166.

［2］陈勇，刘克敏，孙幸福.网络火控中一些亟待解决的关键技术［J］.火力与指挥控制，2011，36（6）：5-7.

［3］陈杰，陈晨，夏元清，等.网络化防空火控系统中的航迹融合［J］.控制理论与应用，2009，26（9）：977-982.

［4］黄义，汪德虎，黄景德，等.近程高射速反导舰炮武器系统大闭环校射新方法［J］.舰船科学技术，2011，33（4）：106-109.

［5］戴耀，汪德虎，胡江.舰炮对空闭环校射新方法研究［J］.电子学报，2006，34（12）：2491-2493.

［6］姜本清，何友.用于闭环校射系统雷达跟踪弹丸的弹丸运动模型［J］.火力与指挥控制，2000，25（6）：11-14.

［7］粱冠辉，程远增，王春平，等.高炮自适应校射算法的研究与实现［J］.火力与指挥控制，2012，37（7）：157-160.

［8］郭治.现代火控理论［M］.北京：国防工业出版社，1996.

［9］汪德虎.舰炮火控原理［M］.北京：国防工业出版社，2009.

Research on Quasi Closed Loop Fire Control Based on Virtual Miss Distance Prediction

WU Ying-feng，LI Wen-cai，WANG Chang-cheng
（1.Unit 63961 of PLA，Beijing 100012，China；2.NO 58 Research Institute of China Ordnance Industries，Mianyang 621000，China）

Abstract：As the traditional closed loop fire control lacks timeliness，and the miss distance cannot be measured easily，a method for quasi closed loop fire control based on virtual miss distance prediction is proposed in this paper.First，the estimation algorithm of the projectile initial state is given with the angle measurement that provided by double observation stations.Then，a prediction model of virtual miss distance is founded based on exterior ballistic theory.Moreover，the estimation algorithm of shoot emendation and the process of quasi closed fire control are analyzed.It shows that the proposed method can avoid the direct detection of miss distance and improve the timeliness of closed loop fire control.

Key words：antiaircraft gun，fire control，virtual miss distance，quasi closed loop fire control

作者简介：吴映锋（1972-），男，江苏东台人，硕士研究生。研究方向：高炮武器系统的作战使用与论证。

收稿日期：2015-03-18修回日期：2015-05-11

文章编号：1002-0640（2016）03-0101-05

中图分类号：TP212.9

文献标识码：A