基于SVM-UPF的雷达弱小目标检测前跟踪算法*

秦占师，张智军，曹晓英，陈　稳

（空军工程大学航空航天工程学院，西安　710038）



基于SVM-UPF的雷达弱小目标检测前跟踪算法*

秦占师，张智军，曹晓英，陈稳

（空军工程大学航空航天工程学院，西安710038）

摘要：针对低信噪比条件下雷达弱小目标的检测与跟踪，提出了基于支持向量机和无迹粒子滤波的检测前跟踪算法。该算法采用无迹卡尔曼滤波生成粒子滤波的重要性密度函数，提高了粒子的使用效率，在此基础上将支持向量机引入到粒子重采样步骤中，通过构建状态的后验概率密度函数来获得多样性的新粒子，有效解决了粒子贫化问题，仿真结果表明，该算法提高了目标的检测概率和跟踪精度。

关键词：检测前跟踪，粒子滤波，无迹卡尔曼滤波，支持向量机

0　引言

检测前跟踪（Track-Before-Detect，TBD）是低信噪比条件下对目标进行检测和跟踪的一种多帧信号积累技术［1］，它在每一帧雷达图像不设检测门限，而是将每一帧的回波信息数字化，并将数据存储起来，然后在各帧数据间对假设路径包含的点作几乎没有信息损失的相关处理，经过多帧积累，在目标航迹被估计出来后，检测结果与目标轨迹同时宣布。近年来TBD技术广泛用于雷达弱小目标的检测和跟踪领域。

目前典型的TBD方法主要有Hough变换法［2］、多级假设检验法［3］、动态规划法［4］和粒子滤波法［5-6］等。基于粒子滤波的TBD（PF-TBD）算法在每帧以目标的出现概率来描述目标的出现状态，在此基础上通过更新的粒子实现目标运动状态的估计，适用于非线性、非高斯情况，是一种真正引入了跟踪的算法。见文献［7-10］。

针对以上问题，本文将无迹卡尔曼滤波（Unscented Kalman Filter，UKF）和支持向量机（Support Vector Machines，SVM）引入到粒子滤波中，利用UKF生成粒子滤波的重要性密度函数，由于UKF将当前时刻的量测融入到系统的状态转移过程中，使得粒子的分布更接近真实的后验概率分布；将SVM引入到粒子重采样步骤中，能获得具有多样性的新粒子，从而有效克服粒子的贫化问题。通过仿真表明，该算法具有较好的检测与跟踪性能。

1系统模型的建立

1.1目标运动模型

假设目标为点目标，在x-y平面内，目标状态方程描述为：

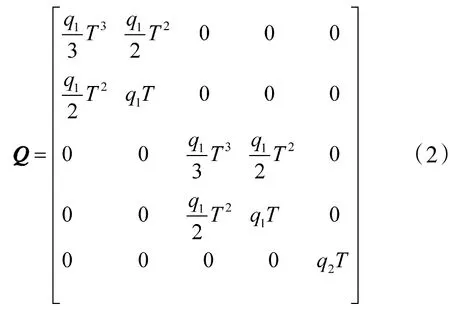
其中：T表示雷达扫描周期，q1、q2分别表示目标运动状态和强度的过程噪声方差。

目标在k时刻的存在状态用Ek来表示。Ek=0表示目标不存在，Ek=1表示目标存在。由此定义目标“新生”概率和“死亡”概率则其马尔科夫转换概率矩阵为：

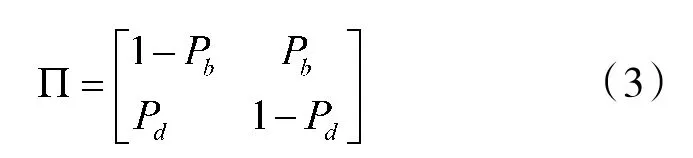
1.2目标观测模型

假设雷达产生一系列整个警戒区域的距离-多普勒图，每一帧图像有m×n个分辨单元（包括m个距离单元和n个多普勒单元）。第k时刻分辨单元（i，j）的观测资料可表示为zk={，i=1，2，…，M，j=1，2，…，L}，时刻的完整测量数据集合表示为Zk= {zi，i=1，2，…，k}。其中为目标的强度量测数据，可表示为：

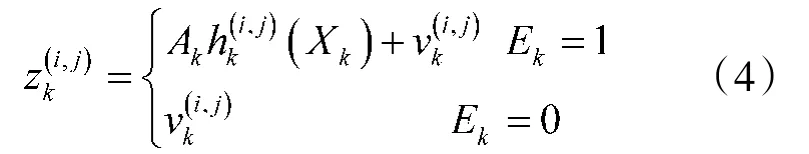
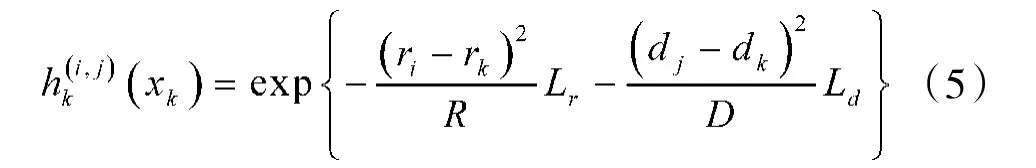
1.3目标模型的似然函数

假设各个分辨单元以及各帧图像之间，量测噪声相互独立，在此前提下，可认为分辨单元内的量测也是独立的，则量测似然函数可描述为：

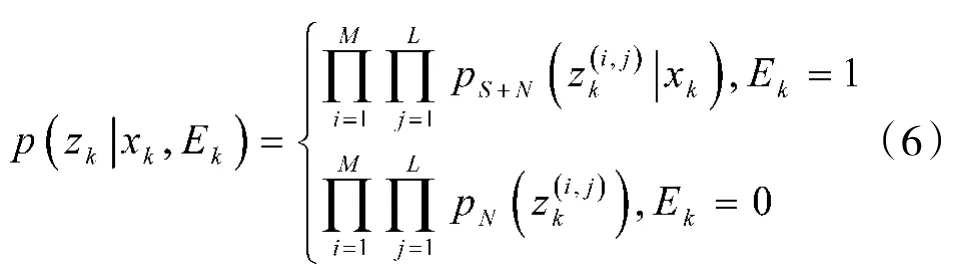
考虑到目标只能对自身及其临近分辨单元的信号强度产生影响，因此，可将似然函数p（zk|Xk，Ek）近似描述为：

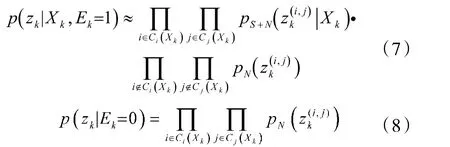
其中：ci（Xk）和cj（Xk）表示受目标回波信号强度影响的距离和多普勒分辨单元（i，j）的集合。

2基于SVM-UPF的检测前跟踪算法

基于粒子滤波TBD算法的基本步骤［11］为：初始化；生成粒子新状态；计算权值并归一化；重采样和目标状态估计。标准PF-TBD算法存在粒子退化问题，为了减少退化现象影响，本文从重要密度函数选择和重采样两个方面进行改进，分别将UKF和SVM引入到PF-TBD算法中。

2.1 UKF基本原理

UKF是S.Julier等人提出的一种非线性滤波方法，它利用无迹变换在估计点附近确定采样，用这些样本点表示的高斯密度近似状态的概率密度函数。算法步骤为：

①初始化

假设初始状态向量为x0，其误差协方差矩阵为P0，则

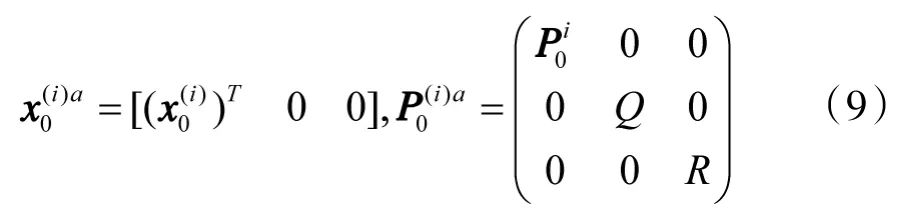
②计算sigma点

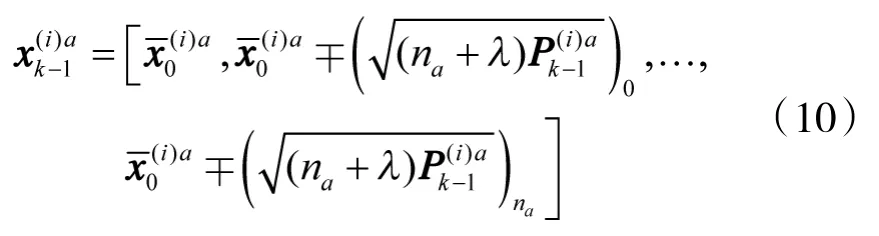
其中，λ为合成比例参数，na=nx+nw+nv。

③时间更新

④量测更新

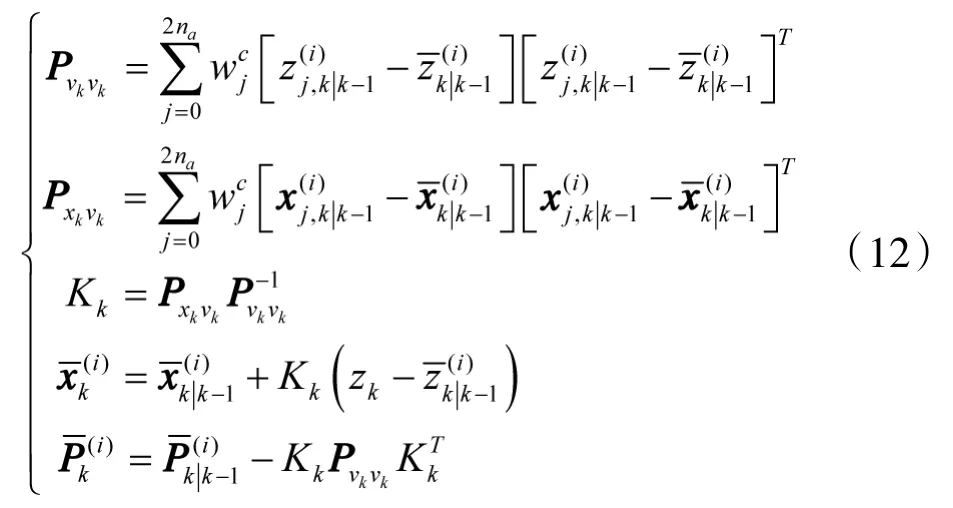
将UKF引入到粒子滤波的算法称为UPF算法，其基本思想是利用UKF构造重要性密度函数，即对k-1时刻的粒子集进行UKF滤波，得到粒子的后验均值和方差用一簇高斯分布构造重要性密度函数，即：

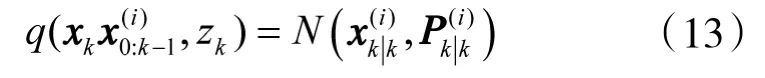
UPF算法融入了新的观测信息，因此，通过UPF更新后，粒子的状态更能反映系统真实的后验状态分布，进而可以抑制粒子退化现象。

2.2基于SVM的重采样方法

支持向量机是一种基于统计学习理论和结构风险最小化原则的机器学习技术［12］，因其具有出色的学习能力以及良好泛化能力，近年来在模式识别、概率密度估计等领域得到了广泛的应用。

根据概率密度的定义，要从样本中估计概率密度，需求解如下方程［13-14］：

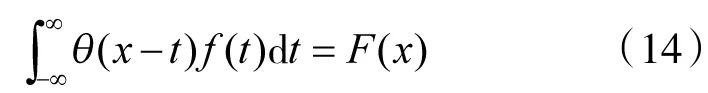
方程（14）的解需在如下函数集中寻找：

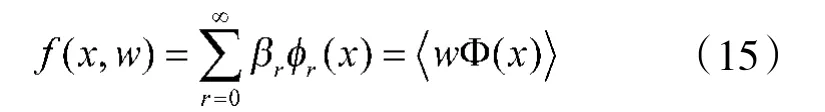
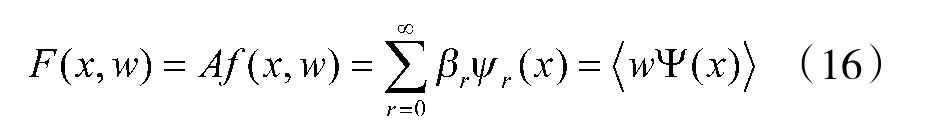
因此，寻求操作数方程的解等同于在像空间中寻找线性回归函数的系数ω。

对于独立同分布样本集{xi，i=1，2，…，l}，其对应的经验分布函数集为{Fl（xi），i=1，2，…，l}。当采用线性SVM和ε不敏感损失函数时，概率密度估计问题等价于如下的数学规划问题［15］：

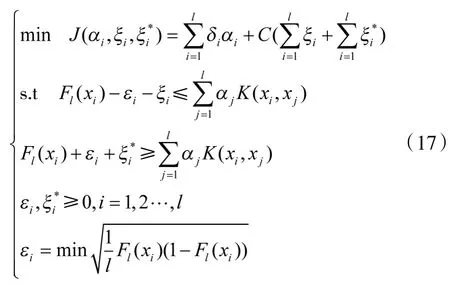
将其代入式（15）可得

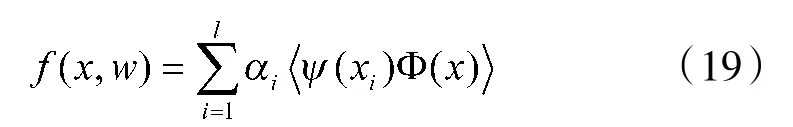
定义像空间中的核函数及交叉核函数分别为

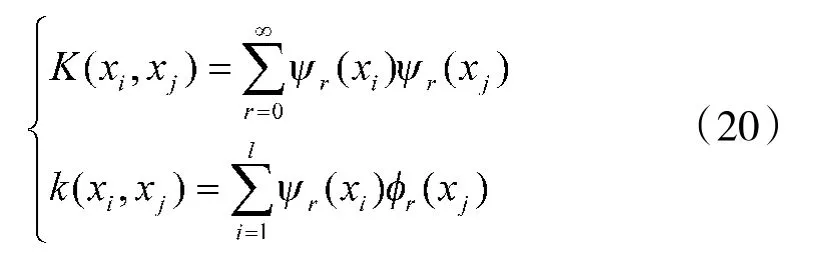
并且对任意x有

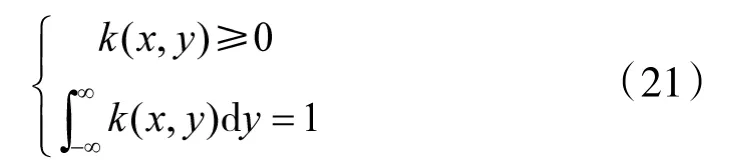
本文采用的核函数以及交叉函数分别为：

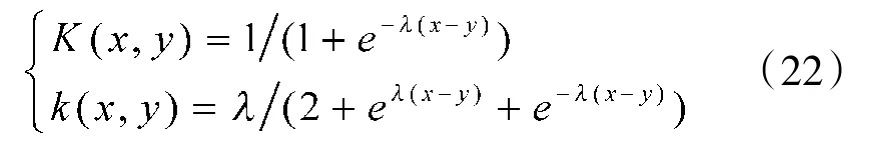
利用交叉核函数可以得到操作数方程的解为：

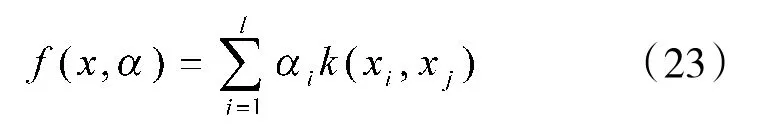
其中系数αi满足：

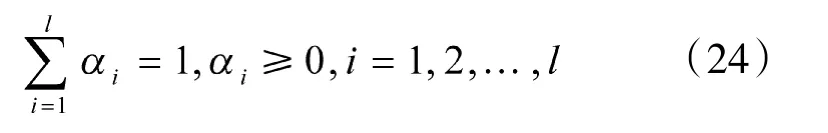
因此，基于SVM的重采样步骤为：

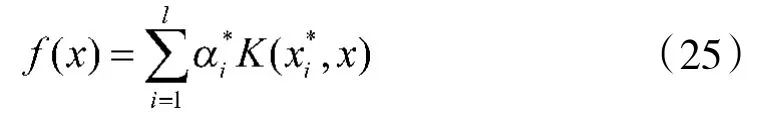
②随机采样。根据状态后验概率密度函数进行随机采样，得到新的粒子集

基于SVM的重采样方法，通过核函数拟合离散分布，得到后验概率密度分布模型，根据此函数进行随机采样可得到多样性的粒子，从而解决了粒子贫化问题。

2.3基于SVM-UPF弱小目标TBD算法

基于上述的讨论，下面给出基于SVM-UPF的弱小目标检测前跟踪算法。假设已知混合状态向量Yk=［XkTEk］T在k-1时刻的联合后验概率密度p（Yk-1|zk-1）可由粒子集来描述。则算法基本步骤如下：

①初始化，设k=0，根据先验分布q（x0）和目标存在的先验概率P（E0=1）产生混合状态样本Yk= ［XkTEk］T；

②更新混合状态样本（Xk，Ek）i，i=1，2，…，N；

对“新生”粒子（满足Eik-1=0，Eik=1的粒子），根据先验分布q（bXk|Ik）采样得到。

对“存活”粒子（即满足Eik-1=0，Eik=1的粒子），利用UKF算法对k-1时刻的粒子状态进行更新，得到重要性密度函数以此重要性密度函数进行采样得到Xik。③计算粒子权值并归一化

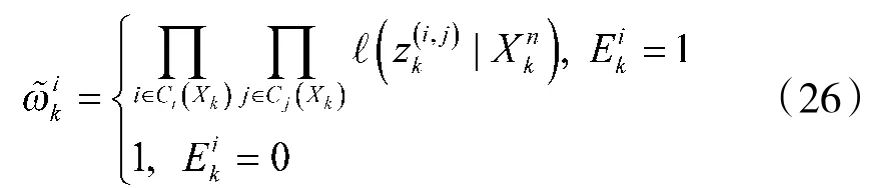
归一化粒子权值：

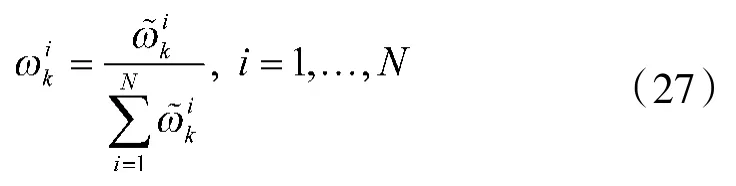
④粒子重采样

计算有效粒子数量Neff，如果其小于预设门限Nth，则利用基于SVM的重采样方法对粒子集重采样得到

⑤计算目标出现概率和估计运动状态

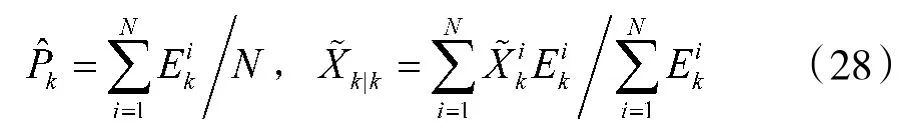
⑥k=k+1，重复步骤②至步骤⑤。

3模拟与分析

假设单个目标作匀速运动，雷达扫描周期T=1 s，一共仿真30个雷达扫描周期，分辨单元数目：m=50，n=50目标从第7帧开始出现，持续到第22帧后消失，目标在第7帧时的状态向量为X7= ［4.2，0.45，7.2，0.25，20］，目标运动状态和强度的过程噪声方差分别为q1=0.001，q2=0.01，量测模型参数R=2 000，D=1，Lr=0.01，Ld=0.01。粒子数N=2 000，“新生”粒子的先验分布q（x0）为：x～U［0，50］，y～U ［0，50］，x˙～U［-3，0］，y˙～U［-3，0］，目标存在的先验概率P（E0=1）=0.05，检测门限设置为0.6。马尔科夫链转移概率Pb=Pd=0.05。蒙特卡罗次数M=1 000情况下进行模拟。

①下页图1为SNR=3 dB和SNR=9 dB情况下，PF-TBD和改进算法的目标检测概率对比曲线。

由图1可知，在不同的SNR下，改进算法的目标检测概率明显高于PF-TBD算法，随着SNR的提高，两种算法的目标检测概率都有所增加；当SNR=3 dB时，两种算法的目标检测概率都较低，当目标出现后，PF-TBD大约有2个时刻的时延，检测概率有一定起伏，而改进算法没有时延，检测概率稳定；当SNR=9 dB时，两种算法的检测概率都有显著提高，且没有检测时延。以上仿真结果表明，改进算法的检测性能优于传统的PF-TBD算法。

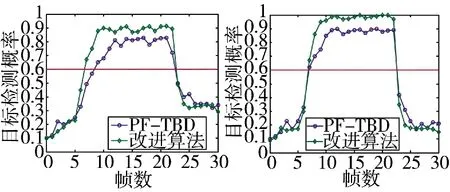
（a）SNR=3 dB　　（b）SNR=9 dB图1　两种算法的目标检测概率

②图2为SNR=3 dB和SNR=9 dB情况下，PF-TBD和改进算法的目标跟踪均方根误差对比曲线。

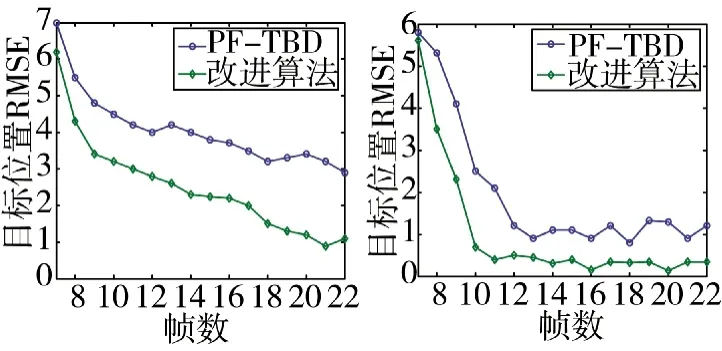
（a）SNR=3 dB　　（b）SNR=9 dB图2　两种算法的目标位置RMSE

由图2可知，不同的SNR下，改进算法的跟踪误差都小于PF-TBD算法，且随着信噪比的提高，目标的跟踪误差逐渐减小；当SNR=3 dB时，改进算法的误差明显小于PF-TBD算法，当SNR=9 dB时，两种算法的跟踪误差都有所减小，且PF-TBD算法趋近改进算法。以上仿真结果表明，改进算法的跟踪性能优于传统的PF-TBD算法，当信噪比较低时，优势更明显。

③表1为信噪比为9 dB时，PF-TBD算法和改进算法的目标位置RMSE均值、方差及平均运行时间比较。

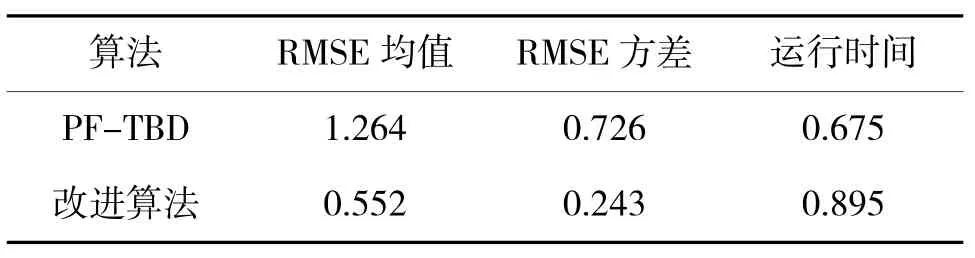
表1　两种算法运行时间

从表1可以看出，改进算法的跟踪精度和稳定性均优于PF-TBD算法。但是，改进算法运算时间较长，因此，提高算法的计算速度是下一步的研究方向。

4　结论

本文提出了一种基于SVM-UPF的检测前跟踪算法。利用UKF算法生成粒子滤波的重要密度函数；在此基础上，本文又将SVM引入到粒子滤波的重采样步骤，通过构建状态的连续后验概率密度模型来获得具有多样性的新粒子，从而有效克服粒子的贫化问题。仿真实验表明，该算法在低信噪比下具有较高检测概率和跟踪精度。

参考文献：

［1］吴孙勇，廖桂生，杨志伟.改进粒子滤波的弱目标跟踪与检测［J］.宇航学报，2010，31（10）：2395-2401.

［2］CARLSON B D，EVANS E D，WILSON S L.Search radar detection and track with the hough transform，part I:system concept［J］.IEEE Trans.On Aerospace and Electronic System，1994，30（1）:102-108.

［3］BLEEKMAN S S.Multistage hypothesis tracking for mdfiple target tracking［J］，Aerospace and Electronic Systems Magazine，2004，19（1）:5-18.

［4］ARNOLD J，SHAW S，PASTERNACK H.Efficient target tracking using dynamic programming［J］.IEEE Trans，On Aerospace and Electronic System，1993，29（1）:44-56.

［5］BOERS Y，DEIESSEN H.Multitarget particle filter track before detect application［J］.IEEE Proceedings on Radar，Sonar and Navigation，2004，151（6）:351-357.

［6］康莉，谢维信，黄敬雄.基于unscented粒子滤波的红外弱小目标跟踪［J］.系统工程与电子技术，2007，29（1）:1-4.

［7］杨小军，潘泉，王睿，等.粒子滤波进展与展望［J］.控制理论与应用，2006，23（2）:261-267.

［8］高山，毕笃彦，魏娜.基于UPF的小目标检测前跟踪算法［J］.计算机应用，2009，29（8）:2060-2064.

［9］张苗辉，刘先省.基于MCMC无味粒子滤波的目标跟踪算法［J］.系统工程与电子技术，2009，31（8）:1810-1813.

［10］杨宁，钱峰，朱瑞.基于遗传算法的改进粒子滤波算法［J］.上海交通大学学报，2011，45（10）:1526-1530.

［11］朱志宇.粒子滤波算法及其应用［M］.北京:科学出版社，2010.

［12］蒋蔚，伊国兴，曾庆双.基于SVM数据融合的实时粒子滤波算法［J］.系统工程与电子技术，2010，32（6）:1334-1338.

［13］张聪，高磊，李少军.基于改进HFQC滤波的红外弱小目标检测［J］.四川兵工学报，2015，36（5）:137-140.

［14］VAPNIK V N，MUKHEJEE S.Support vector method for multivariate density estimation［C］//Advances in Neural Information Processing Systems,Cambridge:MIT Press，2000.

［15］WESTON J，GAMMERMAN A，STITSON M O，et al.Support vector density estimation［C］//Advances in Kernel Methods-SV Learning，Cambridge:MIT Press，1999.

Track-before-Detect Algorithm for Radar Weak Target Based on Support Vector Machines Unscented Particle Filter

QIN Zhan-shi，ZHANG Zhi-jun，CAO Xiao-ying，CHEN Wen
（School of Aeronautics and Astronautics Engineering，Air Force Engineering University，Xi’an 710038，China）

Abstract：An improved Track-Before-Detect（TBD）algorithm based on support vector machines and unscented particle filter is proposed for weak target detection and tracking in low Signal to Noise Radio（SNR）environment.The improved algorithm uses the Unscented Kalman filter to generate the important proposal distribution which can match the true posterior distribution more closely.On this basis，the article introduces support vector machines into particle resampling.By building the posterior probability density model of the states，diversiform particles can be gained.And the impoverishment problem is solved effectively by these diversiform particles.The simulation results show that the improved algorithm can improve probability of detection and tracking accuracy.

Key words：track-before-detect，particle filter，unscented Kalman filter，support vector machines

作者简介：秦占师（1989-），男，山东菏泽人，硕士研究生。研究方向：雷达信号处理及工程应用。

*基金项目：陕西省电子信息系统综合集成重点实验室基金资助项目（201107Y03）

收稿日期：2015-03-05修回日期：2015-05-07

文章编号：1002-0640（2016）03-0048-05

中图分类号：TN957

文献标识码：A