基于GARCH模型的股票市场风险度量

柯希均

（湖北咸宁职业技术学院，湖北 咸宁 437100）

基于GARCH模型的股票市场风险度量

柯希均

（湖北咸宁职业技术学院，湖北 咸宁 437100）

国内外预测股指股票市场风险基本采用对波动性估计具有精度、准确度和可信度较高的GARCH模型族。本文用沪深300和标普500两组指数构建GARCH（1，1）模型，计算两组指数的VaR值。将GARCH（1，1）模型同相应EGARCH、TARCH模型进行比较，并结合所计算出的VaR值，揭示两地金融资本市场的差异。

GARCH模型；风险度量；VaR

GARCH模型是一个为金融时间序列量体订做的回归模型，可以有效地追踪金融时间序列收益率的动态方差，特别适用于波动性的分析和预测，这样的分析对投资者的决策能起到非常重要的指导性作用。大量实证研究表明，金融市场收益率分布具有“尖峰厚尾”的特性，如果使用正态分布进行估计会损失大量尾部信息。鉴于金融时间序列的波动集聚性和分布的“尖峰厚尾”性，Nelson和Hamilton分别用广义误差分布（GED）与t分布来调整尾部的偏差；而VaR（Value at Risk：在险价值）的提出，使市场风险能够更为直观地表现出来。本文用GED分布来拟合GARCH（1，1）模型，并计算VaR（Value at Risk：在险价值）来度量金融市场风险。

一、文献综述

1、GARCH模型

自从Engle（1982）提出ARCH模型分析时间序列的异方差性以后，T·Bollerslev（1986）又提出了GARCH模型。GARCH模型是在ARCH模型基础上对方差的表现形式进行了直接的线性扩展，弥补了在优先样本下ARCH模型阶数过大所带来的计算效率和精度上的不足。

为了衡量收益率波动的非对称性，Glosten、Jagannathan与Runkel（1989）提出了GJR模型，在条件方差方程中加入负冲击的杠杆效应，但仍采用正态分布假设。

Nelson（1991）提出了EGARCH模型。Engle等（1993）利用信息反应曲线分析比较了各种模型的杠杆效应，认为GJR模型最好地刻画了收益率的杠杆效应。

Glosten、Jagannathan与Runkel（1993）分析比较了各种GARCH-M模型，指出不同的模型设定会导致条件方差对收益率产生正或负的不同影响。

2、VaR

G30集团在研究衍生品种的基础上，于1993年发表了标题为《衍生产品的实践和规则》的报告，提出了度量市场风险的VaR（Value at Risk：风险价值）。

J.P.Morgan推出Risk Metrics风险控制模型，主要用于计算VaR。

Philippe Jorion（1996）详细地介绍了VaR的定义、一般计算方法，并总结了各种计算VaR方法的特点。通过实证分析，对比正态分布和t分布下的静态模型计算VaR值的区别。

二、理论依据

1、GARCH模型原理

一般的GARCH模型可以表示为：

其中，xt是1×（k+1）维外生变量向量，酌是（k+1）×1维系数向量。式（1）给出的均值方程式是一个带有误差项的外生变量函数。由于是以前面信息为基础的一期向前预测方差，所以被称作条件方差，式（1）也被称作条件方差方程，包含3个组成部分：常数项琢0：用均值方程的扰动项平方的滞后来度量从前期得到的波动性的信息。（ARCH项），上一起的预测方差（GARCH项）。

2、VaR模型原理及估计方法

VaR方法的核心在于描述金融时间序列的统计分布或概率密度函数。通常我们以价格或指数的对数收益率序列为描述对象。若使用价格、指数序列，则我们描述该金融时间序列的统计分布过程中就会受到一定的限制，因为价格或指数的取值范围为[0，+∞]。另外，对数收益率Rt的取值范围位于整个实数域，且多期对数收益率是单期对数收益率的和。

考虑一个证券组合，假定P0为证券组合的初始价值，R是持有期内的投资回报率，在期末证券组合的价值为：P=P0（1+R）。

假定回报率R的期望和波动性（通常用标准差来描述）分别为μ和滓。若在某一置信水平琢下，证券组合的最低价值为P*=P0（1+R*），则根据VaR的定义，证券组合偏离均值的非预期损失为VaR，公式为：

VaR琢=E（P）-P*=P0（1+μ）-P0（1+R*）=P0（μ-R*）

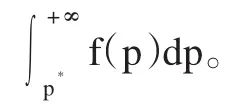
3、VaR估计的方差—协方差法

方差一协方差方法是基于对数收益服从正态分布的假设，在此基础上用历史数据来度量均值、标准差、相关系数等主要参数的方法。

三、实证分析

1、数据选取

本文选取的研究对象：沪深300指数开盘价，样本区间为2011年4月1日至2014年1月10日；美国标准普尔500指数开盘价，样本区间为2013年8月19日至2016年8月18日。鉴于两地股市开盘日期的不一致，因此，将样本区间调整为两地共同开盘日的日收盘价，调整后样本个数同为712。

数据来源于大智慧行情软件，使用软件为Eviews7.1及Excel2010。

2、描述性统计

由时序图可以看出，两组时间序列显然都为非平稳序列。对日开盘价取对数收益率Rt，其表达式为：Rt=lnPtlnPt-1。Pt为指数当日开盘价，Pt-1为指数前一日开盘价。

（1）沪深300和标普500的偏度均与0有一定差异，拒绝均值为0的原假设，不符合正态分布的特征。

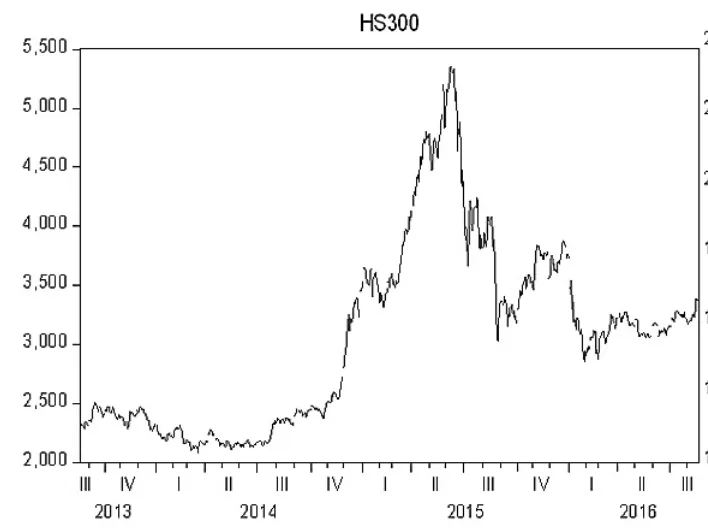
图1 沪深300指数日开盘价时序图

图2 标普500指数日开盘价时序图

图3 沪深300收益率时序图

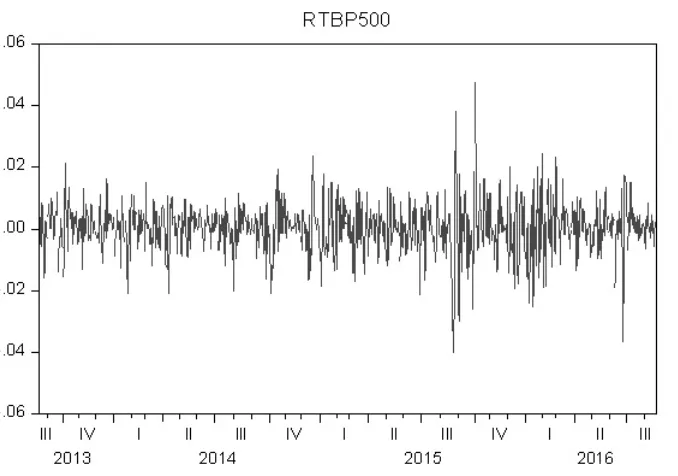
图4 标普500收益率时序图

图5 沪深300日收益率残差时序图

图6 标普500日收益率残差时序图

（2）标准正太分布的峰度K应为3，沪深300（K=7.557889＞3）和标普500（K=6.173763＞3）收益率曲线的分布凸起程度大于标准正态分布，说明存在较为明显的“尖峰厚尾”形态。

（3）沪深300收益率的JB统计量为718.82，标普500收益率的JB 统计量为302.5816，两者均大于5%的显著性水平上的临界值5.99，所以可以拒绝其收益分布正态的假设，并初步认定其收益分布呈现“厚尾”特征。

3、序列的单位根检验

观察收益率序列的图形。

检验结果显示两个序列均是平稳的。

4、检验ARCH效应

观察沪深300和标普500收益率的自相关图，可以看出无自相关性，因此直接将两者对常数回归得到残差序列。观察残差平方的自相关图，分别对两序列进行LM检验。

沪深300指数和标普500指数日收益率残差序列具有集群效应，大波动集后接连大波动集，小波动集后连着小波动集。沪深300ARCH效应检验P值为0.0138，标普500ARCH效应检验P值为0.0000，均不能拒绝不存在ARCH效应的原假设。

表1 沪深300指数GARCH模型残差LM检验

表2 标普500指数GARCH模型残差LM检验

5、估计模型参数

对两组日收益率进行检验后，可以看出序列呈平稳性、自相关性不显著、残差序列存在ARCH效应。因此，可以对序列模拟GARCH 模型。为了判断均值方程中是否加入风险度量项，对两组数据分别进行了含M项的GARCH模型的拟合。拟合后沪深300指数、标普500的GARCH项系数均显著，因此保留M项。各估计系数满足非负性，在10%的水平下显著。

6、检验残差的自相关性和正态性

通过观察残差的自相关图和残差平方的自相关图，我们可以认为两组指数GARCH模型的残差序列、残差平方序列均不存在自相关性。由正态分布检验可以看出两组残差序列均不具有正态性。

可以看到，两组指数GARCH模型残差均不存在ARCH效应，拟合出的GARCH 方程组都已很好的消除了条件异方差效应。因此，上述模型能够较好的反映沪深300指数和标普500指数的收益率序列异方差现象。

所得GARCH（1，1）模型方程如下：

沪深300指数

标普500指数

四、VaR计算

所用VaR公式如下：VaR=-Pt-1Z琢滓t。通过前面的分析，我们知道收益率的分布明显不符合正太分布，因此，我们假设其服从GED分布。

设期初时刻的W值为1，采用GARCH标准差的均值计算，时间间隔为一天。即计算一天期的VaR值，同时用GARCH标准差的最大值和最小值计算VaR极大值和极小值。

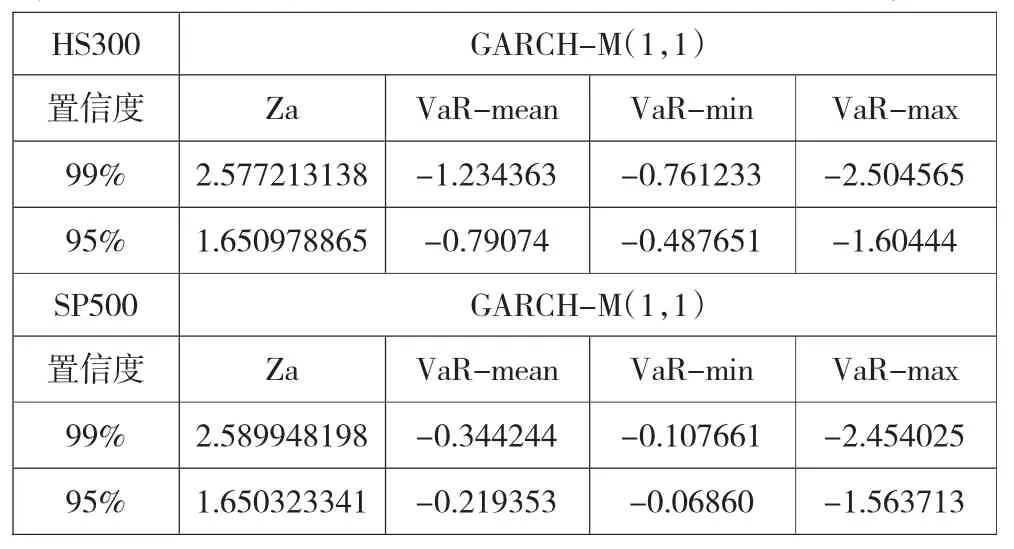
表3 两种指数在GED分布下的不同模型的VaR估算结果

五、结论

本文通过对沪深300和标普500收益率序列的GARCH模型模拟，建立VaR风险评估模型，可以得到以下几点结论。

第一、沪深300和标普500收益率密度分布不是正态分布，而是具有明显的“尖峰厚尾”的特征。这可能是因为投资者对市场的预期和风险偏好不同，导致对收益率的预期也不一样，并且投资者对于信息的反应具有滞后性。

第二、通过建立不同的GARCH模型可以发现，不论是美股市场还是大陆市场，负向冲击对市场的影响要大于正向的冲击，在实际中表现为利空使股市下跌的幅度大于利好使股市上涨的幅度。在TARCH和EGARCH模型中，标普500杠杆项的系数均大于沪深300杠杆项系数，这说明美国金融市场对信息反馈的非对称效应更强，投资者对坏的信息反映会更加敏感。换言之，美国金融市场相对于中国金融市场，在对股市波动性的反映操作上更为成熟灵敏。

第三、从VaR估计结果来看，标普500的VaR值始终小于沪深300的VaR值，这说明中国内地股市风险要高于美国股市。

[1] 胡利琴：金融时间序列分析实验教程[M].武汉大学出版社，2012.

[2] 张穹宇：基于GARCH-VAR模型的股票市场风险度量研究[J].东方企业文化·财会金融，2013（9）.

[3] 谢军军：VaR风险度量方法在股票市场的应用研究 [D].华中科技大学，2006.

[4] 任甄、吴雷：GARCH（1，1）模型波动率预测的实证研究[J].金融观察，2010（11）.

（责任编辑：徐悦）

咸宁职业技术学院校级一般课题项目，金融中介发展与产业结构优化的实证研究，编号：2016B006。