圆锥曲线中定点问题剖析



圆锥曲线中定点问题剖析

◇福建陈龙

在高考的试卷中与圆锥曲线相关题目往往是压轴题之一,是高考的难点问题.在圆锥曲线中有一类有关动直线过定点的问题往往是命题的热点．这类问题与圆锥曲线中的其他类型问题不同,它不存在常规解法,只有比较笼统的解题思想，即定点问题必然是在变化中能够表现出的不变量,也就是用变量表示问题中诸如直线方程、数量积、比例关系等表达式,从而能够从表达式中分析出不受变量影响的某个点．但这种模糊的解题思想对于学生而言,就缺少了一个明确的抓手,在处理相关问题时,学生往往不知如何下手．因此，有必要对这类问题进行理论和实践的全面剖析．

1理论剖析:解题思想解读,归纳解题方法

圆锥曲线中有关定点的问题有很多种类,其中考查最多的一类是动弦过定点的问题,这类问题的解题思想很明确:将问题中的直线方程用某个变量表示出来,分析直线方程中不受变量影响的某个点,即为所求定点．解题的思想虽然很简单,但突破这类问题有一个关键点,即变量的选择．如何选择变量及选择什么样的变量，会使题目的解题过程呈现不同的思路及解题方法．众所周知,确定一条直线需要2个要素:斜率和一点或者直接知道2点,结合动弦过定点的解题思想,显然这里为解题中变量的选择提供了一定的思路,即在通常的处理过程中往往是从直线的斜率或点的坐标入手以其为中间变量,寻找不变量．而变量选择的不同,也就为我们解决问题提供了2类不同的处理方式.

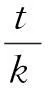
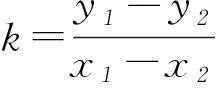
上述2种解题思想,虽然采用了不同的中间变量,但解题的思路其实是理出一脉,其实质为引进变化的参数来建立直线方程,换句话说即利用变量来书写动弦所在直线方程,然后通过直线方程的变形,来确定方程中与参数无关的定量来得出定点．

2实践操作:理论指导实践,明确解题方向

根据解题思想,分析出的解决方法,然而理论的分析应当为实践解题服务,以明确问题解决的方向,故而文章以一道调研试题为例,剖析上述理论在实践中具体运用和注意事项．

∠OFA+∠OFB=180°．

(1) 求椭圆方程;

(2) 当A为椭圆与y轴正半轴的交点时,求直线方程;

(3) 对于动直线l,是否存在一定点,无论∠OFA如何变化直线l都经过此定点．

方法1以直线方程为突破.

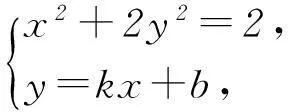
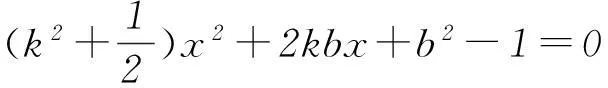
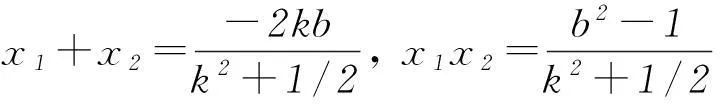
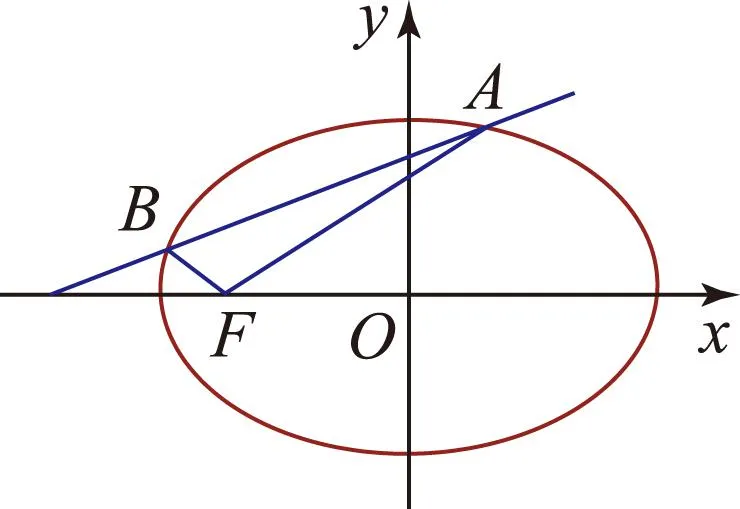
图1

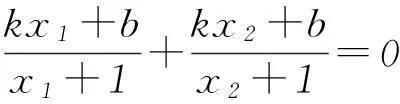
方法2以点的坐标关系为突破.

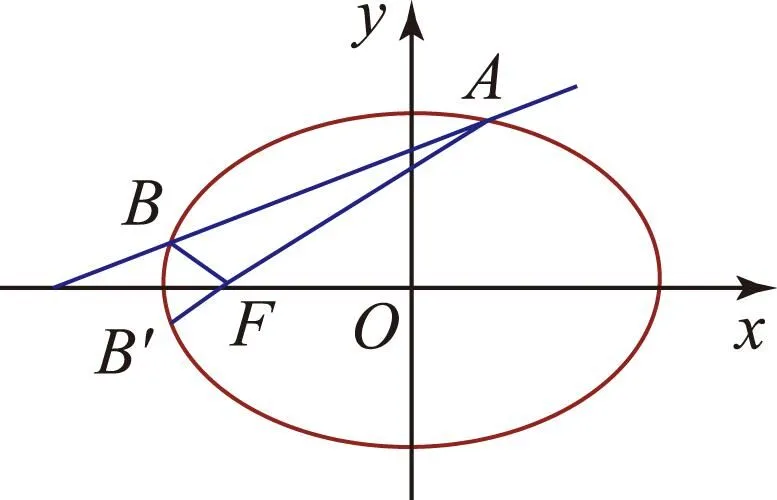
图2

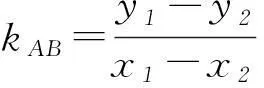
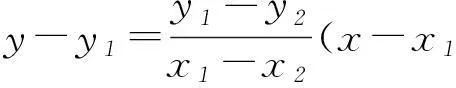
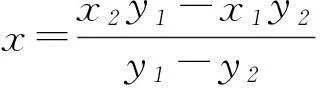
设直线AF的方程为y=k(x+1),所以

y1=k(x1+1),-y2=k(x2+1),

所以

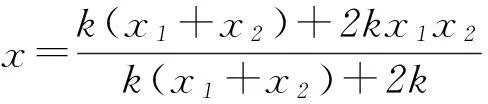
①

将直线AF：y=k(x+1)代入到椭圆方程可得

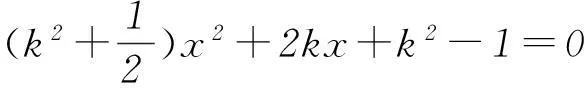
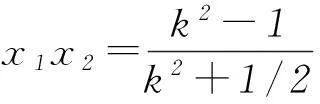
将x1+x2和x1x2代入式①可得x=-2,所以动直线恒过(-2,0)．

综合分析上述实践操作的过程,笔者认为动弦过定点的问题其本质上归类到直线与圆锥曲线位置关系中,无论是利用直线方程化二元为一元,还是利用点的坐标之间的关系寻找不变量,其解决过程中均利用了根与系数的关系,因此,在解决此类问题时利用交轨法是解题的重要手段之一．

(作者单位：福建泉州培元中学)