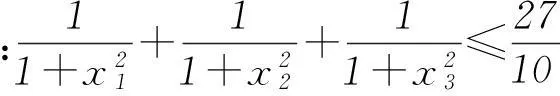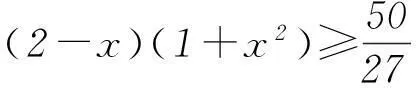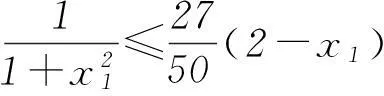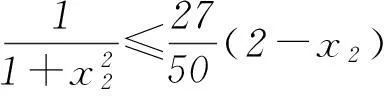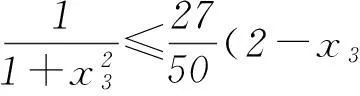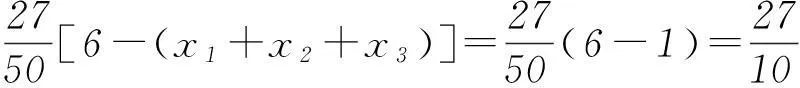数学题的创新解法，贵在反思与领悟



数学题的创新解法，贵在反思与领悟

◇甘肃吴冠瑛

解题实践表明:熟知解题过程中的一些易错点、失分点,有利于将错误消灭在萌芽状态,避免走弯路,提高解题的针对性、实效性.具体解题中应如何有效避错呢？

1要重视对“基本知识”的理解

A锐角三角形;B直角三角形;

C钝角三角形;D以上均有可能

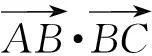
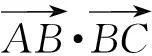
剖析对向量夹角的概念及锐角三角形的性质没有理解到位.

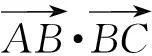
反思1) 向量夹角须满足2个向量的起点重合(若不重合,可通过“平移”实现). 2) △ABC为锐角三角形的充要条件是3个内角都是锐角.

2要重视对“隐含条件”的深度挖掘

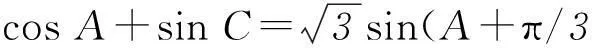
剖析没有充分利用一个三角形为锐角三角形的充要条件.

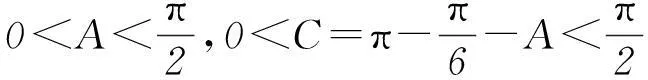
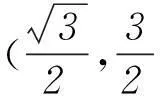
反思1) 本题不但要对cosA+sinC准确变形,而且最为关键的是要准确分析内角A的取值范围. 2) 利用△ABC为锐角三角形的充要条件是不等式0

3要重视对“联系观点”的理解与运用

第(1)问通过求导分析函数的单调性,即可求得函数的最小值.

剖析因放缩过大导致不能解决目标问题.

正解(1) 所求最小值为50/27 (具体过程,略).

又易知0

于是,将上述同向不等式两边分别相加得

故得证.

反思本题第(2)问,大部分同学没有考虑第(1)问与第(2)问之间的紧密联系,即缺乏灵活运用“联系”的观点去分析、解决问题的思想意识.

(甘肃省教育科学“十二五”规划课题GS[2014]GHB0978)

(作者单位：甘肃靖远县第四中学)