明确复习重点探索有效途径——2016 年高考数学第2 轮复习建议(下)



明确复习重点探索有效途径
——2016 年高考数学第2 轮复习建议(下)

◇北京丁益祥(特级教师)

2.3通过揭示知识本质发展理性思维

数学学科具有概念性强、充满思辨性的特点.求解数学问题时,若能对数学概念进行充分辨析,真正理解它的作用,往往能产生质的飞跃.

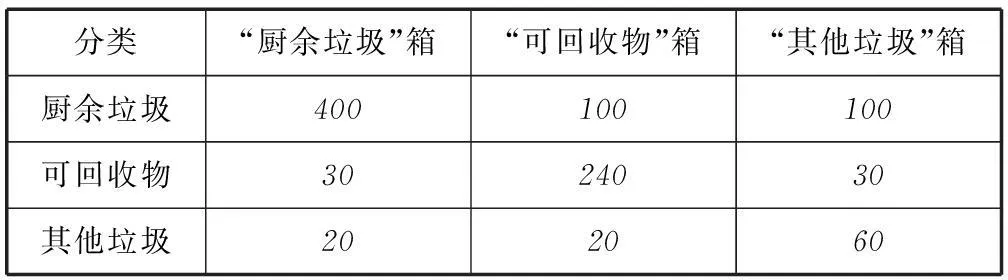
表1　单位: t

(1) 试估计厨余垃圾投放正确的概率;

(2) 试估计生活垃圾投放错误额概率;

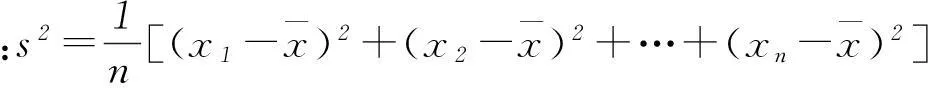
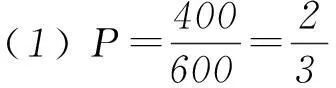
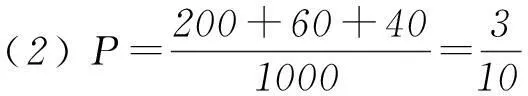
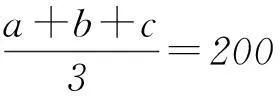
从形式上看,上式表明:方差s2是3个变量a、b、c的三元二次函数,从函数角度直接求方差s2的最大值显然是困难的.为此,我们不妨换一个角度思考问题,分析方差的本质意义和作用:方差是衡量一组随机变量集中和离散程度的统计量.随机变量越集中,方差越小;随机变量越离散,方差越大,反之亦真.至此,注意到a、b、c中a>0,因此我们自然让a=600,b=0,c=0,此时3个数据a、b、c离散程度最大,从而方差s2最大,(s2)max=80 000.

概率统计问题在高考应用问题中最为常见.然而,此题与以往常见的概率统计问题有着明显的不同:一是数量关系以表格的形式来呈现;二是对生活垃圾投放正确或错误的标准没有明确的文字说明;三是考查方差的最大值而不是考查考生熟悉的方差的最小值,并且形式上表现为三元二次函数的最大值.求解中由于对方差的意义缺乏本质的认识,因此只能从形式上把问题归结为三元二次函数的最大值,进而导致对问题的求解束手无策.

事实上,方差是衡量一组离散型随机变量集中和离散程度的统计量.随机变量越集中,方差越小;随机变量越离散,方差越大,反之亦真.这是求解第(2)问的立足点.即欲使方差最大,需且只需3个数据a、b、c最离散.而这只有建立在对概念本质深刻理解的基础上,才能获得上述理性的认识.第2轮复习中,若能适当地选择一些着重考查知识本质特征的问题进行训练,学生的理性思维水平必将得到很好的发展.

2.4通过综合问题求解培养学科能力

高考中对知识的综合考查,主要体现在6个解答题中,但历年的选择题或填空题中,也有小题综合化的趋势.高考中通过这些综合问题的考查,着重检测学生的数学能力.而第2轮复习的一个重要任务是提高学生的能力,因此,必须注意通过综合问题求解训练,达到提高学生能力的目的.

(1) 求椭圆C的方程;

(ⅱ)求△ABQ面积最大值.

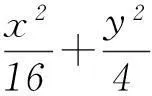
问题(2)的第(ⅱ)问,先画出图形如图4.欲求△ABQ面积最大值,原则上应求出△ABQ的面积函数,再求最大值.然而△ABQ的面积函数不易直接建立,因此应另想办法.

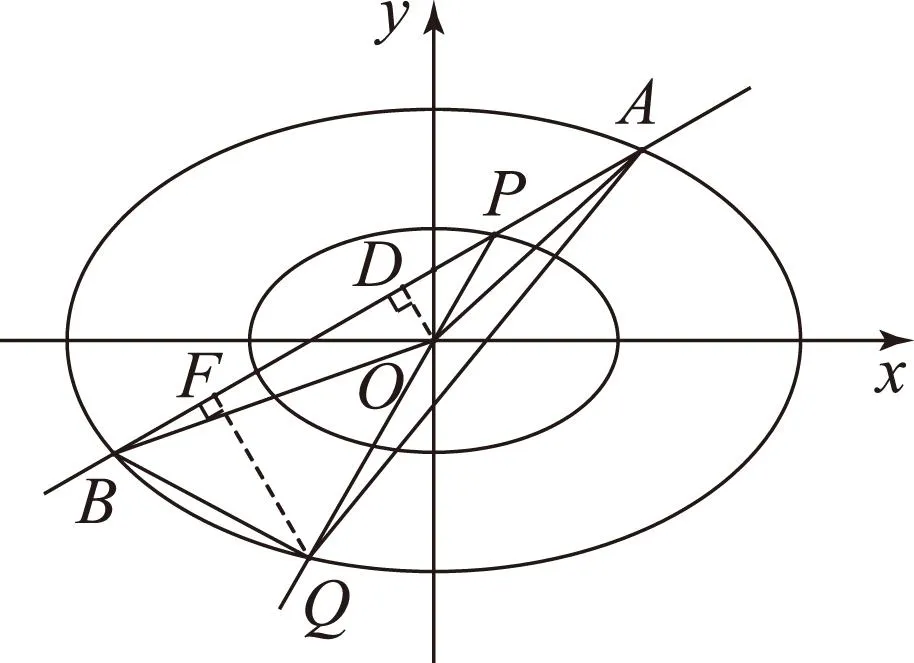
图4

为此,我们把直线y=kx+m代入椭圆E的方程得x2+4(kx+m)2=16,整理得

(1+4k2)x2+8kmx+4m2-16=0.

设A(x1,y1)、B(x2,y2),则

由Δ=64k2m2-16(4k2+1)(m2-4)=16(16k2+4-m2)>0,得m2<16k2+4.所以

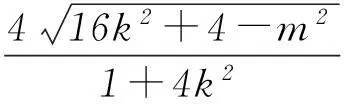
因为直线y=kx+m交y轴于点M(0,m),所以

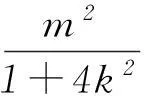
(1+4k2)x2+8kmx+4m2-4=0.

2.5通过经典问题研习、弘扬传统文化

我国是世界最具文明的国度之一,具有5000年的悠久历史.在我国数学发展的耀眼星河中,不乏经典名题.恰当地精选一些历史名题作为复习素材,可以极大地弘扬传统文化.

图5

A14斛;B22斛;

C36斛;D66斛

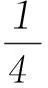
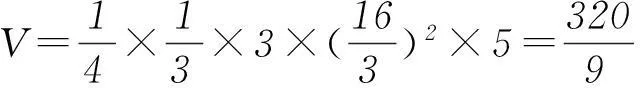
现今流传的《九章算术》,是指三国时期刘徽为《九章算术》所作的注本,它是《算经十书》中最重要的一部可以与西方《几何原本》相媲美的世界数学名著,距今已有2000余年的历史.选择此题作为高考试题,旨在体现对传统文化的继承和发扬.

近年来,我国正大力倡导弘扬传统文化,从这个层面上讲,上述问题既展示了数学从古到今巨大的应用价值,又体现了我国数学研究的悠久历史和璀璨夺目的厚重文化.

(作者单位：北京陈经纶中学)