求解函数方程的利器——“算两次”



○解题研究○

求解函数方程的利器
——“算两次”

陆建根

(江苏省镇江中学，212017)

函数方程是数学竞赛中的重要内容,在近几年的高校自主招生考试中也有所涉及,一般难度较大,求解的要求较高.函数方程的问题难在已知条件很少,很多问题的已知条件只有一个等式,而且条件比较抽象,无法进行常规的运算.这就要求我们要充分利用已知条件,尽可能地去分析一个表达式的两重含义,也即利用“算两次”得到新的等式或新的条件去解决问题，这种方法在函数方程的求解中应用极为普遍.本文就求解函数方程时具体该如何去实施“算两次”谈一些个人的体会,供参考.

一、利用原式迭代“算两次”,得到新的等式

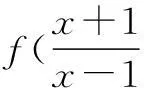
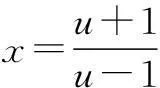
评注有些复杂的函数方程问题通过再“算”一次还不能解决问题,这时需要再“算”两次或者n次才能求解.

例2解函数方程

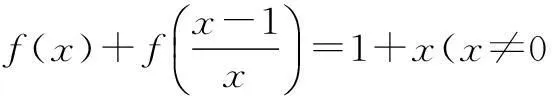
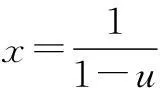
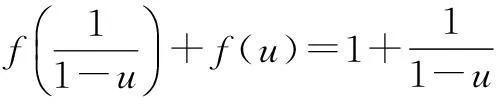
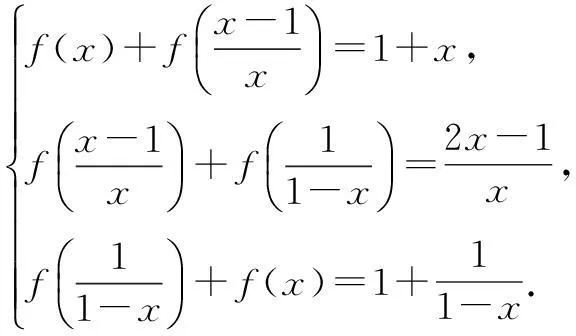
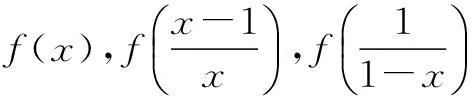
例3(2008年清华大学自主招生试题)

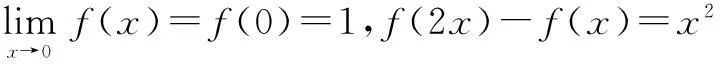
分析跟例1一样,由一个方程f(2x)-f(x)=x2是无法直接求f(x)的表达式的,需要利用f(2x)-f(x)=x2构造新的等式.

解由题设条件，得

……,

将上述等式左右两边分别相加,得

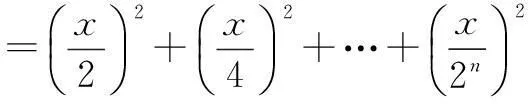
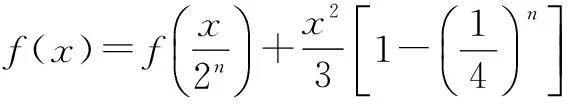
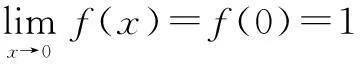
评注这里实际上是利用已知等式f(2x)-f(x)=x2算了n次,得到n个不同的等式,相加后求得f(x)的表达式,这有点类似于数列中的裂项相消.在函数方程的求解中,构造类似于数列中裂项相消的等式,通过求和来求f(x)的表达式的问题有很多.

二、利用不等式“算两次”,得到新的等式

例4(2002年全国高中数学联赛试题)已知f(x)是定义在R上的函数,f(1)=1,且对任意x∈R都有f(x+5)≥f(x)+5,f(x+1)≤f(x)+1,若g(x)=f(x)+1-x,则g(2 002)=______.

分析已知条件中最关键的是两个不等式,而要求的是g(2 002),显然要利用不等式设法得到等式.

解因为g(x)=f(x)+1-x,所以

f(x)=g(x)+x-1.

由f(x+5)≥f(x)+5,得

f(x+5)=g(x+5)+(x+5)-1

≥f(x)+5=g(x)+x-1+5；

由f(x+1)≤f(x)+1,得

f(x+1)=g(x+1)+(x+1)-1

≤f(x)+1=g(x)+x-1+1,

即g(x+5)≥g(x),g(x+1)≤g(x).

所以g(x)≤g(x+5)≤g(x+4)

≤g(x+3)≤g(x+2)

≤g(x+1)≤g(x),

所以g(x)=g(x+5)=g(x+4)

=g(x+3)=g(x+2)

=g(x+1)=g(x),

则g(2 002)=g(1)=f(1)+1-1=1.

三、利用条件等式的对称性“算两次”,得到新的等式

例5(2004年全国高中数学联赛试题)设函数f:R→R满足f(0)=1,对于任意x,y∈R都有f(xy+1)=f(x)f(y)-f(y)-x+2,求f(x).

分析显然原等式左边关于x,y对称,右边不关于x,y对称,这样通过x,y互换可以得到一个新的等式.这里实际上是利用左式的对称性对f(xy+1)“算”了两次.

解因为f(xy+1)=f(x)f(y)-f(y)-x+2,x,y互换,得

f(yx+1)=f(y)f(x)-f(x)-y+2.

上述两式左边相等,所以右边也相等,所以f(x)f(y)-f(y)-x+2=f(y)f(x)-f(x)-y+2,整理得

f(x)-x=f(y)-y.

令y=0,则f(x)=x+f(0),

所以f(x)=x+1.

四、挖掘已知等式内涵“算两次”,得到新的等式

例6函数f(x)是定义在N*上并在N*上取值的递增函数,并且满足条件f(f(x))=3x,试求f(1)+f(9)+f(96)之值.

解由已知等式，得

f(f(f(x)))=f(3x).

考察上述等式左边,利用已知条件f(f(x))=3x,考虑上述等式左边代数式的外面两重“f”,把最里面的f(x)看成自变量x,可以得到f(f(f(x)))=3f(x),这样我们就得到一个新的等式

f(3x)=3f(x).

如果f(1)=1,则f(f(1))=f(1)=1,利用f(f(x))=3x,再“算”一次,得f(f(1))=3×1=3,矛盾,所以f(1)≠1.

设f(1)=a,a>1,但f(f(1))=f(a)=3,因为a>1,所以3=f(a)>f(1),所以f(1)=2.

所以f(3)=3f(1)=6,f(6)=f(f(3))=3×3=9,f(9)=3f(3)=3×6=18,

f(18)=3f(6)=3×9=27,f(27)=3f(9)=3×18=54,f(54)=3f(18)=3×27=81,f(81)=3f(27)=3×54=162,f(162)=3f(54)=3×81=243.

由于162-81=81,243-162=81,所以自变量在81,162之间的正整数取值时的自变量与函数值之间是一一对应的,所以f(96)=162+15=177,

所以f(1)+f(9)+f(96)=2+18+177=197.

评注可以发现,上述解法中最关键的是根据条件得到一个更简洁的等式f(3x)=3f(x).而得到这个等式的关键是对f(f(f(x)))算了两次,一方面它等于f(3x),另一方面它也等于3f(x).解决问题的另一个关键点:f(1)=2也是通过“算两次”得到的.

五、不一样的“算两次”,得到一样的结果

例7求出所有的函数f(x):R→R,使得对于所有a,b∈R,都有f(a·f(b))=ab.

解法1因为f(a·f(b))=ab,

①

令a=1,得f(f(b))=b.

②

对①式两边取“f”，得

f(f(af(b)))=f(ab).

③

利用②式对③式左边再“算”一次,得

f(f(af(b)))=af(b),

所以f(ab)=af(b)；

④

在④式中令b=1,得

f(a)=af(1)；

⑤

利用⑤式对①式左边再“算”一次,得

f(af(b))=af(b)f(1)=abf(1)f(1),

所以abf2(1)=ab,

即f2(1)=1,f(1)=±1.

若f(1)=1,则f(a)=a,若f(1)=-1,则f(a)=-a,也即,若f(1)=1,则f(x)=x；若f(1)=-1,则f(x)=-x.

解法2利用单射.

因为f(a·f(b))=ab,

①

令a=1,得f(f(b))=b.

②

若b1≠b2,则f(f(b1))≠f(f(b2)),得f(b1)≠f(b2),所以函数f(x)为R→R上的单射(即自变量不同,函数值也不同).

由①得f(a·f(b))=ab=ba=f(bf(a)),因为该函数为单射,所以af(b)=bf(a).

令b=1,得f(a)=af(1)，

以下同解法1.

解法3利用满射.

因为f(a·f(b))=ab,

①

令a=1,得f(f(b))=b.

②

显然上式右边的b可以取任意实数,函数f(x)为R→R上的满射,所以至少存在一个实数b1,使得f(b1)=1.

在①式中令b=b1,则f(a)=b1a,

从上述分析可以看出,“算两次”虽然不是一种具体的可以操作的方法,但是给出了遇到新的问题时思考的方式:选择一个适当的量,一方面……另一方面……综合可得……就是去选择一个恰当的量,研究这个量的两个或多个方面,从而得到一个或多个等式.在不同的环境中这个量可以是不同的,可以是一个代数式,可以是一个方程,也可以是不等式.“算”出的另一个方面则可以是新的代数式、新的方程、新的不等式,有时也可以是和“数”相对应的“形”. “算两次”的实质是从不同的角度来考察同一个量,这实际上是我们系统、全面地认识数学问题必须具备的数学素养,也是我们认识世界应该具备的一种能力.