挖掘活力因素 创设高效课堂



挖掘活力因素创设高效课堂

朱华峰

(浙江省杭州余杭高级中学，311100)

高中数学是一门重要的基础课程.它不仅要求学生掌握基础知识与基本技能,而且要求教师不断培养学生数学思维方法和用数学知识解决实际问题的能力．但是,由于高中数学本身的特点以及初高中数学的跨度较大,让学生普遍感到高中数学难学,进而产生畏惧心理,甚至产生厌学的情绪．因此,如何提高学生的学习兴趣与快乐感,激发学生学习数学的热情,创设高效的数学课堂,成为广大数学教师的首要任务．

一、保持活力,创设轻松氛围

如何让学生不再对数学课感到害怕,让学生喜欢数学老师，喜欢数学课,让其一天不上数学课就有一种“一日不见如隔三秋”的感觉呢?要做到这一点，最重要的是要求数学教师本身要保持活力．一个充满活力的数学教师善用幽默的语言和形象的比喻,使数学课堂气氛“活”起来．适时运用幽默的教学手段和语言来调节课堂气氛,有利于缓解压力,使枯燥的课堂教学过程变得灵活生动,也可以稳定学生的心态,使学生以一个更好的状态投入数学学习中来．教师要放下架子,与学生建立平等的师生关系,尽可能在教学中营造融洽的学习氛围,拉近师生间距离．教师要善于发挥自己的课堂语言、肢体语言魅力来吸引学生,引导学生思维,让学生学得有趣,提高教学效果．让学生喜欢数学老师从而喜欢数学课堂,最终喜欢数学这门学科．

案例1高一的起始课讲到的内容是集合,学生对交集与并集的符号总是搞混掉,笔者就会打个比方:大家看交集与并集的符号“∩”和“∪”,我们把它们看作下雨天放在外面的两只碗,大家看看哪只碗里的水会多些呀?显而易见是“∪”,那么很明显了,它就好比并集运算,元素不会比交集少!

现代教学论认为，课堂教学除知识对流的主线外,还有一条情感对流的主线，即课堂教学活动是师生之间知识和情感的双边交流活动.学生在与教师的交往和沟通中能发现更多学习中的快乐,这种快乐就是他们喜欢数学、学好数学的主动性因素．

二、精心预设,激发学习兴趣

教师的主阵地在课堂,预设是课堂教学的基本要求,是学生生成的起点．高质量的预设是教师发挥组织者作用的重要保证,它有利于教师从整体上把握教学过程,使教学能有序展开,从而激发学生的学习兴趣,提高学生学习活动的效率．所以，要求教师对每一节课必须要有足够的认识和把握,精心预设好教学预案,使之更好地符合学生的实际．课前“预设”是为了“更好的生成”而预设的重点不是教师如何去教,而是预设学生如何去学.预设时应考虑:学生在课堂上可能有哪些生成,如何引导学生得到有价值的生成,如何为学生创造一个开放而广阔的思维空间,让学生的思维在这个广阔的空间里自由飞翔,并迸发出思维的火花．

案例2在讲解一元二次方程根的分布问题时,给出这样一个题目:

已知方程x2+(2k-1)x+k2=0,若方程有两个大于1的根,求k的取值范围．

可以联立不等式求解.

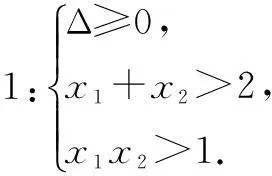
师:我们解方程、解不等式都需要找等价条件.学生1给出的是两个都大于1的必要条件，而不是充分条件，不等价，因而上面的解法不完整．

生2:画图象!

师:好方法!我们可以研究对应的函数f(x)=x2+(2k-1)x+k2的图象,让我们来尝试这种办法．(学生画函数图象)

师:根据图象,我们需要列几个限制条件,才能解决问题?

学生不断补充,最后确定三个条件

师:如果缺少其中一个条件,会怎样?

引导学生得出三种不满足条件的情况．

师:这种方法确实很好,能不能加以推广?如果问题改为:“已知方程x2+(2k-1)x+k2=0,若方程在x∈(1,2)上有两个根,求k的取值范围．”限制条件还怎么列? (学生研究,得出结论)

师:用图象解决根的分布问题,是一种很有效的方法．那么韦达定理到底能不能解决第一个题目?我们知道:“方程有两个大于0的根”的等价条件是

我们是不是可以根据学生1的思路，找出满足题设条件的充要条件呢？

由x1>1,x2>1，有x1-1>0,x2-1>0引导学生得出结论:

教师：大家归纳一下两种方法适用的题型．

“预设”的目的就是为了帮助学生发现问题并提出问题,是把问题充分地暴露出来而不是掩盖下去,是引导学生对问题进行分析、研究,最终使学生依靠自己的聪明才智来解决问题,同时使学生的创新意识和创造能力得到培养．

三、师生互动,调动学习激情

教师不再只是知识的传授者, 而应该是学生学习的合作者、引导者和参与者, 师生互动意味着平等对话, 教师由居高临下的权威向“ 平等中的首席”转变．在课堂教学中,笔者一直提倡“自由发言”, 学生大多会在相互讨论和争论中得出比较正确的答案, 一些原先沉默寡言的学生也会受到这种氛围的感染, 情不自禁地站起来发表意见．我们应建立和谐融洽的师生关系, 让学生在宽松的气氛中学习, 敢于表现、 敢于质疑、敢于争论，学生的思维、情趣、个性特点有了张扬的空间并得以实现.在具体教学中,我还利用学生好动的特点,按内容设计了“以玩促学”“以动促学”“以竞促学”“以帮促学”等活动,设置解题竞技、游戏等方式,激发学生竞争意识,引导学生参与变题、编题. 学生通过自己的思考,能享受变题、编题带来的成功感,调动了学生学习的热情．

案例3复习函数单调性内容时,有这样一个例题:已知函数f(x)的递增区间是[-2,3],求函数y=f(x+5)的递增区间．

学生很快就能求解:

方法1整体代换,令-2≤x+5≤3,解得-7≤x≤-2,递增区间为[-7,-2].

方法2图象平移,y=f(x+5)图象是由y=f(x)图象左移了5个单位得到．

教师:那么如果老师把题目改编成这样:“已知函数f(x)的递增区间是[-2,3],求y=f(x+5)+4的递增区间．”该如何求解了?

(有学生在区间两端盲目加上4,得到递增区间为[-3,2],有学生认为增区间仍然为[-7,-2])

教师:大家再想想,这个数字4到底有什么意义?

学生:恍然大悟!上下平移对单调区间不产生影响,答案是[-7,-2].

教师:谁能对这个题再改编一下,考考大家?

学生踊跃发言,出现很多形式,归纳如下:

题1求y=f(-x+5)+4的递增区间；

题2求y=f(|x+5|)+4的递增区间；

题3求y=|f(x+5)|+4的递增区间.

先让全班同学一起做,然后引导学生讨论分析,得出以下结论:

生3：对于题1，根据复合函数单调性求法,只能得到递减区间,令-2≤-x+5≤3,解得2≤x≤7,递增区间为[2,7].

生4： 对于题2，首先考虑y=f(|x|)的增区间,y=f(|x|)的图象在x≥0时,保留了y=f(x)的图象,故其递增区间为[0,3],因此y=f(|x+5|)+4的递增区间为[-5,-2].

生5：对于题3，条件不够无法完成,因为首先考虑y=|f(x)|的递增区间时,y=|f(x)|图象是保留y≥0时y=f(x)的图象,需要增加f(x)=0的信息.

教学活动是教师与学生之间双边互动与交流发展的过程．现代课程标准倡导师生之间“教学合一”、“教学互动”的双向活动形式．因为有学生作为主角的参与,才会有学生对问题认识的逐渐丰富,课堂也就成了学生交流智慧的空间,在凸显和激发学生的主动性、独立性和创造性,活跃课堂教学氛围等方面,作用和影响显著而深刻．有效、深入的互动交流,有助于高中生主体特性的有效展示,有助于交际能力的有效培养,有助于学习能力的有效锻炼．

四、巧置作业,凸显个性发展

在整个数学教学过程中,以备课为始,作业设计为终．在课堂学习过程中,学生的学习情况具有个别差异性,因此对待学习状况不同的学生必须区别对待,不能一刀切．如果教师采取的是一刀切的形式,无视学生的水平差异,这样导致的后果是优秀的学生感觉“吃不饱”,后进生“吃不了”．学生之间的两极分化会越来越严重,必然会扼杀了一部分学生学习数学的兴趣．那些优秀的学生并没有在完成既定的作业之后,主动地再去寻求新的作业,往往是完成就万事大吉,从而限制了他们潜能的发展．而“吃不了”的学生则为了完成作业,会出现抄袭的现象,这样的形式对他们的发展和进步没有任何的作用．因此,作为教师,我们要针对不同学生的个性、潜能等设置不同标准的作业,激发他们对数学的兴趣,让充满魅力的数学课堂的余温能够保持下去．因此,我在为学生布置作业的时候,除了选做题,经常会设计几个开放型的思考题.

例如，在函数章节，请有能力的同学,为我们函数单元检测卷命两个备用试题．

在向量章节，学习了平面向量的正交分解,那么大家知道有笛卡尔斜坐标系吗?请大家查阅相关资料,并尝试完成以下问题:

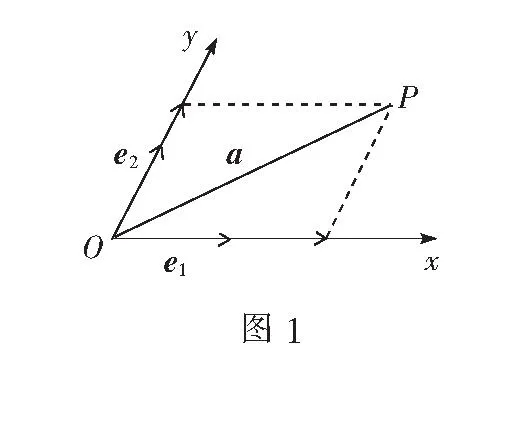
“教者有心,学者得益．”作业是课堂教学的延伸,作业个性化设计,可以最大限度地拓展学生的减负空间,让学生有更多的时间自由支配,丰富课余生活,实现个性化的发展,从而不断提高数学学习的效率.

课堂上,当我们充分挖掘活力因素,尽力为学生创造一个“海阔凭鱼跃,天高任鸟飞”的课堂境界时,他们会在这片天地中尽情地展现自己,和谐、愉悦的课堂氛围得以营造,高效的数学课堂得以创设,教学效果也得以达成．作为数学教师,我们要努力让每一个学生都喜欢“玩数学”,让每一个学生在数学上都得到不同程度的发展.

师:很好!思考问题一定要全面．

(教师在黑板上板书两直线垂直时的结论:当直线斜率都存在且不为零时,l1⊥l2⟹k1k2=-1;当一条直线斜率不存在时,l1⊥l2⟹另一条直线斜率为零.)

师:上面,我们从两直线垂直得到了直线斜率的关系,那么,上述结论反过来成立吗?请同学们先独立思考,然后在小组内讨论．