浅析与圆交汇的几类问题



浅析与圆交汇的几类问题

郑玉梅

(江苏省扬州市邗江区公道中学，225119)

直线与圆是几何的基础,解决此类问题常运用数形结合的思想方法．本文通过对与圆相关的几类典型问题的求解，探索其中隐含的一般规律，以期抛砖引玉.

一、与圆有关的最值问题

例1在平面直角坐标系中,A、B分别是x轴和y轴上的动点,若以AB为直径的圆C与直线2x+y-4=0相切,则圆C面积的最小值为______.

解法1∵∠AOB=90°,∴O在圆C上,求圆C面积的最小值,等价于求圆半径的最小值r0．

如图1，设直线2x+y-4=0与圆C相切于点H,则有CO+CH≥OH(当且仅当O、C、H三点共线时取等号),即OH与2x+y-4=0垂直时圆C的半径取最小值，有2r0=OH.

解法2设直线2x+y-4=0与圆C相切于点H,则点C到点O的距离等于C到直线2x+y-4=0的距离,∴点C在以O为焦点,以直线2x+y-4=0为准线的抛物线上，C为抛物线顶点时圆C半径取最小值r0.

由于O到直线2x+y-4=0的距离

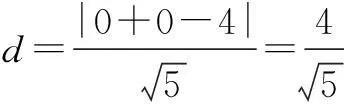
评注此题是与圆有关的面积最值问题,上述解题思路均是利用圆的几何性质将问题转化,熟练掌握圆的几何性质是根本．

二、与圆有关的参数范围问题

例2已知过点P(m,2)作直线l与圆O:x2+y2=1交于A,B两点,且A为线段PB的中点,则m的取值范围为______.

分析1此处P、A都是动点,若先固定P,将P放在直线上较远的地方,作直线与圆相交,直线越靠近圆的边缘,弦AB越短,PA、AB不可能相等；将AB向圆心靠近,AB变长(最长是直径),故点P不会离圆心很远，将点P沿直线靠近圆,不难找出临界位置.

解法1∵A是PB的中点,圆x2+y2=1的直径是2,由题意,PA=AB对AB∈(0,2]有解,∴PA≤(AB)max=2(PA取最小值时AB为直径,P、O、A三点共线，如图2、3).

由PA≤2,得点P到原点距离小于等于3,因此有

m2+4≤9,

分析2从代数角度考虑,设点,转化为方程有解问题．

解法2设A(x1,y1),B(x2,y2),

∵A是PB的中点,

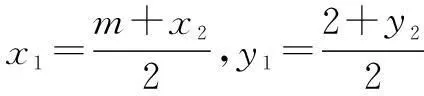
即x2=2x1-m,y2=2y1-2.

∵A(x1,y1),B(x2,y2)在圆x2+y2=1上,

两式相减,得AB方程为:

4mx1+8y1-m2-7=0.

因为直线AB与圆有交点,所以d≤r,即

∴m4-2m2-15≤0,

∴(m2-5)(m2+3)≤0，

评注此题将参数范围问题转化为直线与圆的位置关系问题.解法2突出了用代数方法研究几何问题的思路,体现了数形结合的重要数学思想方法．本题还可以通过拓展训练,将定直线改成圆,A是PB的中点改成PA=2AB等,提出如下变式引导学生思考.让学生通过变化的背景,探求这类问题的本质特征,运用数形结合的思想分析和解决问题,由

数思形,以形想数．

变式1若存在点P(m,2),使过点P所作直线l与圆O：x2+y2=1交于A、B两点，且PA=2AB,求m的范围.

变式2若圆C2:(x-3)2+(y-4)2=m2上存在点P,使得过P的直线与圆O：x2+y2=1依次交于A、B,且满足PA=2AB,求m的范围.

三、圆与不等式的交汇问题

例3设m,n∈R,若直线(m+1)x+(n+1)y-2=0与圆(x-1)2+(y-1)2=1相切,则m+n的取值范围是______．

简解因为直线与圆相切,所以

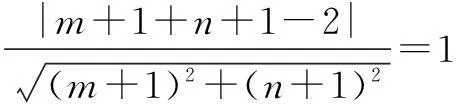
即1+m+n=mn.

于是有

解之得

评注圆与不等式的交汇实质上反映了圆的独特性质,即圆内点、圆外点的性质;直线与圆相交、相离的性质;圆与圆的相交、相离的性质等,这些问题反映在代数上就是不等式的性质.此题以直线与圆的位置关系给出参数之间的数量关系,利用基本不等式转化,题意新颖独特,既调动了学生学习的积极性和主动性,又使得“过程、结论并重，知识、能力、思想方法并重”．

总之,处理直线与圆、圆与圆的位置关系问题,一般均可以从代数角度(方程解的个数)或几何角度(圆心到直线的距离、两圆的圆心距等)去考虑,充分体现了“形”的直观性和“数”的严谨性．