让解题错误成为一种再生资源——以数列教学为例



让解题错误成为一种再生资源
——以数列教学为例

姚华琴

(江苏省黄埭中学,215143)

数学学习离不开数学解题,学生在解题过程中难免会发生错误．美国心理学家桑代克说过:“学习的过程是一种渐进的尝试错误的过程．”钱学森也说过,正确的结果是从大量的错误中得出来的,没有大量的错误作台阶,也就登不上正确结果的高台．如何让学生在错误中成长,让解题错误成为一种宝贵的再生资源，教师首先要读懂学生的错误,再利用纠错的机会去引导学生走出错误的沼泽地．用引申、联想、归纳等手段借题发挥,正确引导,避免就题论题,让学生的“解题错误”转化为课堂教学的有效资源．这样也有利于完善认知结构,深化思维过程,从而增强和提高解题能力．

一、 善待偏差,顺势迁移

差错人皆有之,学生在学习中难免存在一定的偏颇、缺陷和失误,教师要善待学生的错误,尽可能挖掘“错解”中的合理成分,因势利导,纠正错误,拓展知识内涵,激发学生的学习兴趣．

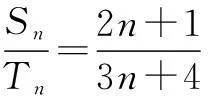
错解1设Sn=2n+1,Tn=3n+4,求得a8=S8-S7=2,b8=T8-T7=3,从而

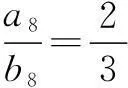
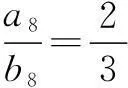
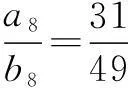
链接(1)利用通项与和项的关系,结合等差中项，可得

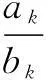
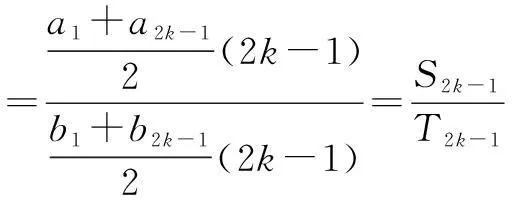
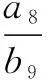
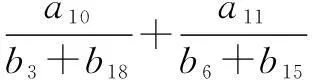
通过正确的引导与拓展让学生掌握知识的本质,解题应注意删繁就简,利用整体思想,使学生的洞察能力和应变能力得到培养．

二、 举一反三,合理联想

前事不忘，后事之师.把自己的错误教训当成一面镜子,认真纠正错题,总结归类，从一个错误中汲取教训,避免一类错误的发生．

例2已知{an}是等比数列,a2=2,a6=8,求a4.

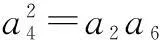
剖析没有考虑等比数列偶数项应同号,a4仅一解,即a4=4.

变式1{an}是等比数列,判断数列{an+an+1},{an+an+2}是否为等比数列?

错解 {an+an+1},{an+an+2}都是等比数列.

剖析 {an+an+1}不一定是等比数列.an+an+1=a1qn-1(1+q),当q=-1时不是等比数列;an+an+2=a1qn-1(1+q2),由于1+q2≠0,所以{an+an+2}为等比数列.

变式2 已知数列{an}是等差数列,{bn}是等比数列,a2=3,b2=3,且a4=b3,b4-b3=m,若数列{bn}唯一,求m的值.

通过对等比数列隐含条件的挖掘,利用变式问题,使学生进一步明确定理、公式和法则的条件、结论以及试用范围,让学生的逻辑推理论证能力和演算能力得到培养．

三、回归定义,避免讨论

数学定义以及基本原理是数学知识再生之源,蕴含特定的数学思想方法．对于一些数学问题,若从最基本的知识点入手,回归定义,可以优化解题过程．

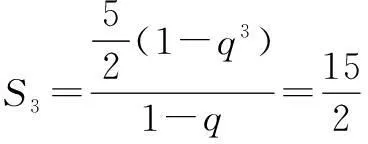
对于涉及等比数列前n项和的问题,若能直接运用已知条件中各个量的关系求解,既可避免分类讨论,又可使问题得到灵活解决．

四、特殊到一般,合理过渡

例4设a1,a2,…,an是等比数列(n≥4),且公比q不等于1,将此数列删去一个数后得到的数列(按原来的顺序)是等差数列,当n=4时,求正数q的值.

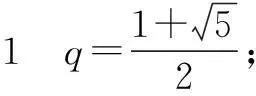
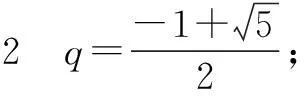
剖析错解1只考虑了a1,a2,a4成等比数列;错解2只考虑了a1,a3,a4成等比数列;错解3只考虑了第一种情况又没有注意到条件“四个正数”中隐含了公比为正数．

链接当n=5,6时q的值为什么?满足条件的n的所有可能值为什么?

剖析n=5时,只能删去a3,由a1,a2,a4,a5构成等差数列,a1+a5=a2+a4,即q4+1=q+q3,因式分解为(q-1)2(q2+q+1)=0,而q2+q+1=0无实数解,q=1又要舍去,所以n=5不合适．当n≥6时,不论删去哪一项,都会出现原数列中连续的三项,由三项既成等差数列又成等比数列,则q=1,所以满足条件的所有n的值为4.

从特殊到一般的思想方法是数列中最基本的思想方法．在解题过程中,首先要学会观察问题,其次分析各个量之间的关系,尽可能地将问题转化为熟知的问题．在研究一般问题“满足条件的n的所有可能值”时,由已经解决的特殊情况n=4出发,情况不明朗时再研究特殊情况n=5,6,研究完特殊情况后,一般情况n的所有可能值也就柳暗花明了．

在教学中,教师要根据自己的教学经验,重视那些容易出错的知识点,做到未雨绸缪,即使学生出现了解题错误,也要采取合适的方式进行处理,让错误成为一种再生资源．只要能找准教学的着力点,针对学生的错误,分析原因,查漏补缺,寻找对策,引申拓展,一定能提高学生的解题能力和数学素养．