铀高压状态方程的第一原理研究*

张其黎，赵艳红，马桂存，张弓木

(北京应用物理与计算数学研究所，北京 100094)

1 引 言

金属铀因其费米面附近的5f电子具有窄带巡游特性，因而具有独特的物理性质。5f能带可使晶体发生类似Peieris或Jahn-Teller的晶格变形，导致能量降低，从而得到低对称、开放的基态结构，通常将这种结构称为α-U结构。

状态方程(Equation of State，EOS)是描述材料热力学性质的基本函数关系，既可以用解析形式表达，即f(T,V,p)=0或f(T,V,E)=0，其中T、V、p、E分别为温度、体积、压强和能量，也可以用数据库和图形来表示。实验上，人们利用活塞-圆筒[1]、金刚石压砧(Diamond Anvil Cell，DAC)[2-6]等静压装置对铀的状态方程和相稳定性进行了研究，发现室温下在不高于100 GPa的压强范围内，α-U结构一直是最稳定的相。当温度高于1 050 K时，DAC实验结果表明：在60 GPa以上，bcc(γ)结构成为稳定的相[7]，该现象与Ⅳ-B族过渡金属Ti、Zi、Ha等类似。铀的熔化行为也与这些过渡金属类似，都是从bcc结构开始。Yoo等人[3,5]利用激光加热DAC实验对铀的熔化曲线进行了测量，压强最高达到100 GPa。要想得到更高压强的实验数据，必须采用动高压技术。动高压技术是利用一次或多次冲击，在很短的时间内使系统的压强快速增加。如果驱动力很强，冲击波将传递到待测样品中，通过测量冲击波速度和样品表面粒子速度，并假设冲击波为平面波，根据质量、动量和能量守恒定律，就可以得到样品波后的压强、密度和能量。从同一初态出发，不同强度驱动加载下的波后状态的集合称作Hugoniot曲线。铀的冲击压缩实验数据可以在很多文献[8-10]中查到，其中包含通过各种冲击加载方式得到的实验结果。

人们利用基于密度泛函理论的第一原理方法对铀的基态性质进行了大量的研究，得到了与实验相符合的平衡体积和弹性模量[11-15]。但是，关于铀的高温相图及状态方程的研究却很少。早期人们采用模型化的广义赝势理论(Modified Generalized Pseudopotential Theory，MGPT)[12]计算有效势，进而获得铀的熔化曲线。这种方法有两个缺点：一是没有考虑5f电子的各向异性，因此不能描述基态α-U结构及低温bcc结构的不稳定性；二是没有考虑电子的热效应。最近Hood等人[16]利用第一原理的分子动力学方法对铀的固相和液相状态方程进行了研究，计算了两种密度下的等容线、Grüneisen参数以及比热，同时还计算了径向分布函数、键角分布函数、电子态密度和流体扩散系数，给出了液体短程有序的证据。

在本工作中，首先利用赝势平面波方法[17]对铀的基态性质进行计算，然后采用量子分子动力学(Quantum Molecular Dynamics，QMD)方法计算密度在19～40 g/cm3、温度在300～10 000 K范围内的状态方程，计算其冲击Hugoniot曲线，并与实验结果及其他理论计算结果进行比较。

2 铀的基态性质

利用VASP程序对铀的4种固态结构(α、bcc、hcp、fcc)的基态性质进行计算，赝势采用PAW-PBE形式，截断能量取为400 eV。α-U结构是面心正交晶系，每个原胞包含两个原子，其基矢为

式中：ey和ez分别为y、z方向的单位矢量；b和c为晶格参数，w为内部参数，在计算中均采用实验值。在hcp结构中，晶格参数c与a的比值(c/a)固定为1.699。对于α、bcc、hcp、fcc结构，不可约Brillouin区的抽样分别采用168、44、150、110个特殊K点。图1显示了不同结构下原子总能随原子体积变化的关系，插图中的实线是对不同结构的多项式拟合，纵坐标表示所有的计算值和拟合值减去α结构拟合值的能量差(ΔE)。从图1中可以看出，当原子体积高于0.012 50 nm3时(压强约为200 GPa)，α-U结构的总能低于其它3种结构。在更小的体积(更高的压强)下，α-U结构的总能高于bcc结构，说明在低压下α-U结构比其他3种稳定，高压下α-U结构不再是稳定的相，与静压实验结果一致。通过拟合得到原子的平衡体积为0.020 35 nm3，体弹模量为131.96 GPa，与实验值(0.020 77 nm3，135.5 GPa)[5]很接近。图2显示了不同结构下压强随原子体积变化的关系。从图2中的插图可以看出，在低压下fcc结构的压强明显高于其他3种结构。

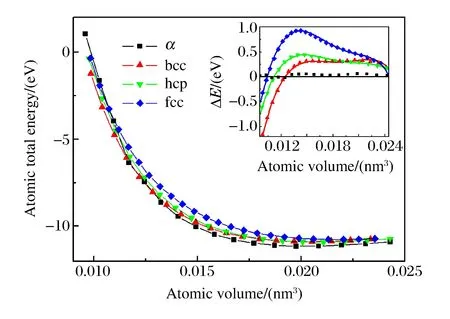
图1 不同结构铀的原子总能与原子体积的关系Fig.1 Total atomic energies vs.atomic volumes for various structures of uranium

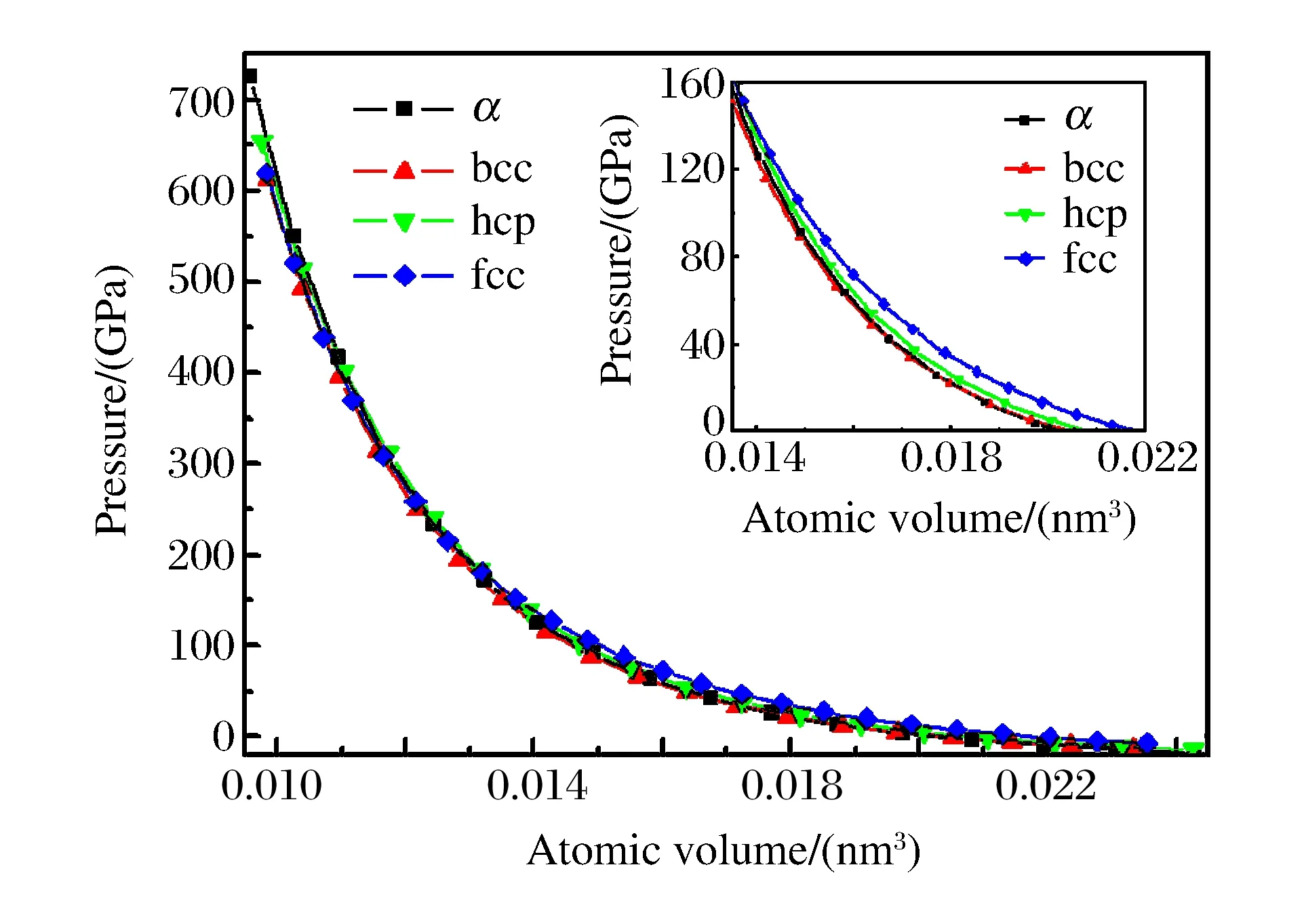
图2 不同结构铀的冷压与原子体积的关系Fig.2 Cold pressures vs.atomic volumes for various structures of uranium

3 有限温度状态方程

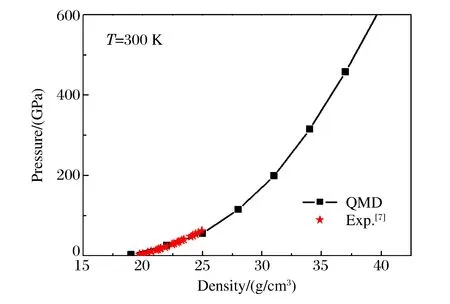
图3 采用QMD方法计算的300 K等温线Fig.3 Isotherm at 300 K calculated by QMD method

采用VASP程序包中的分子动力学程序进行模拟，其中赝势采用投影缀加波(Projector Augmented Wave，PAW)势，交换-关联函数的计算采用局域密度近似(Local-Density Approximation，LDA)。在模拟过程中，为了减少平面波截断误差和有限尺寸效应的影响，截断能量取为1 200 eV(截断误差小于0.5%)，粒子数取54(有限尺寸误差小于1%)，采用正则系综，即系统的粒子数、体积和温度保持不变。离子温度用Nosé-Hoover温度调节器控制，电子的温度效应通过能带占据数的费米分布函数引入。总离子步数取为4 000，最初的1 000步用于系统达到平衡，通过对剩下的离子步数求平均，可以获得状态方程数据。我们计算了密度在19～40 g/cm3、温度在300～10 000 K区间的状态方程数据(p，V，E)。图3显示了T=300 K时铀的等温线，图中同时给出了Dewaele等人[7]利用DAC在T=298 K时测得的实验数据。可以看出：在实验数据范围内，QMD计算结果与实验结果符合得很好。

利用通过QMD法得到的状态方程数据，根据Rankine-Hugoniot关系，可对铀的冲击Hugoniot状态进行计算

式中：E、p、V为终态的状态量，E0、p0、V0为初态的状态量。初态的温度和密度分别取实验值330 K和18.93 g/cm3；初态的压强和能量由分子动力学方法计算得到，分别为3.55 GPa和-4.414 eV。

铀的Hugoniot关系如图4和图5所示，图4为冲击波速度-粒子速度(us-up)关系曲线，图5为相应的Hugoniot压强-密度曲线。

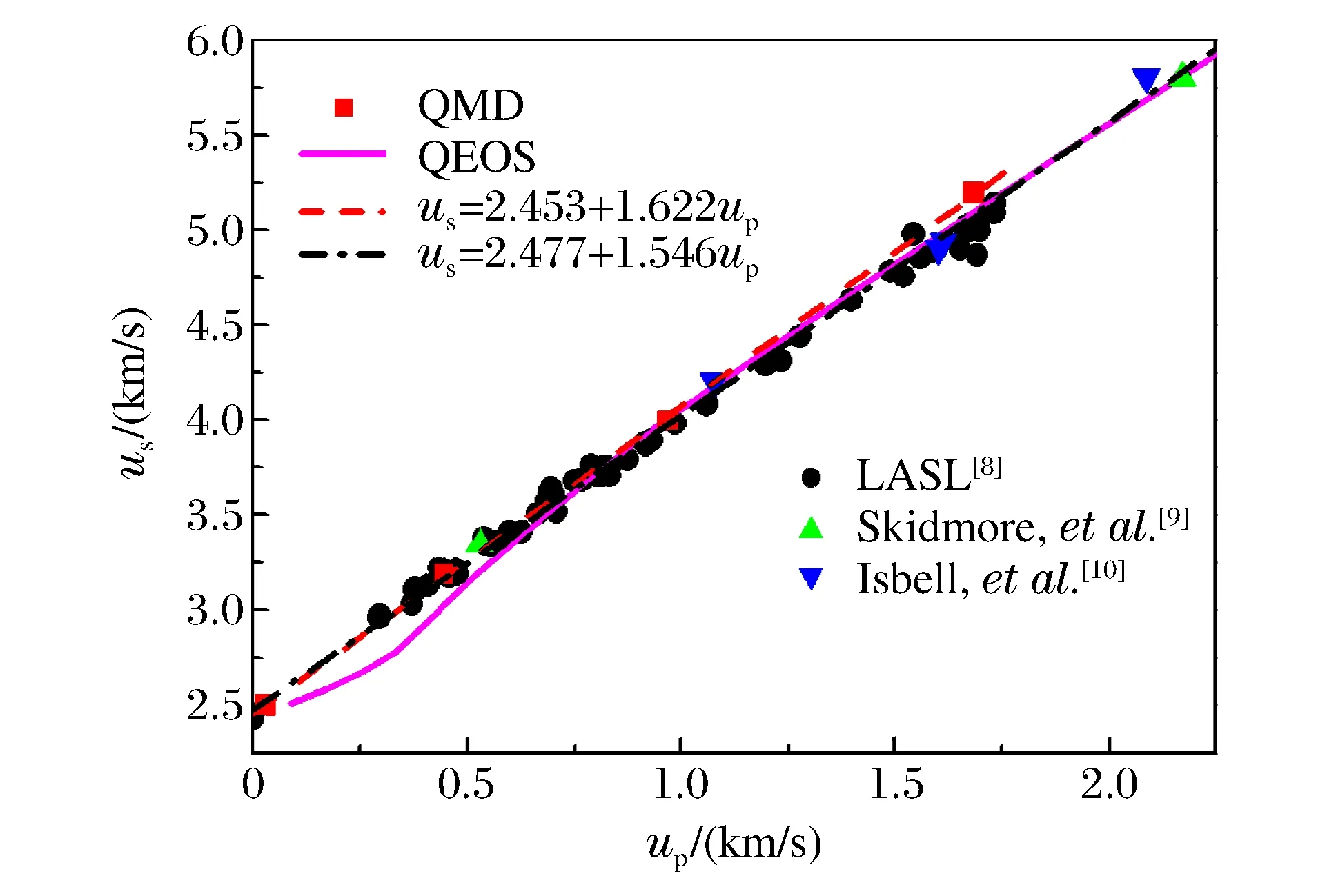
图4 铀的us-up关系曲线Fig.4 us vs.up curves for uranium

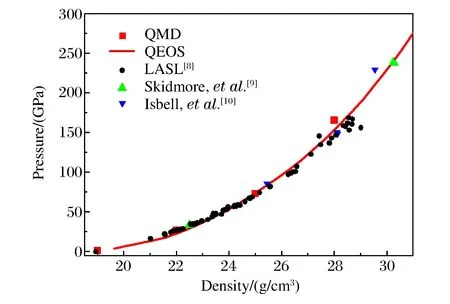
图5 铀的压强-密度曲线Fig.5 Pressure vs.density curves for uranium

采用QMD方法计算了压强小于160 GPa时铀的4个Hugoniot状态点(见图4)，对这4个点进行线性拟合，得到us=2.453+1.622up。图4中还显示了由不同实验装置获得的冲击加载实验数据[8-10]，对所有实验数据进行线性拟合，得到us=2.477+1.546up。在图4中同时给出了利用快速计算状态方程(Quotidian Equation of State，QEOS)模型[17]计算得到的结果。在QEOS模型中，电子热贡献采用Thomas-Fermi模型，离子热贡献采用Cowan的离子物态方程模型，其实质为准谐近似。对比不同方法所得结果可知：在100 GPa以下的压强区域内，QMD计算结果与实验结果符合得很好，与QEOS计算结果差别较大，QEOS方法所得计算结果偏软。由此可以认为，采用准谐近似描述离子热贡献的QEOS模型不能准确描述铀的热力学性质，在实际应用中需要采用更准确的状态方程模型。在100 GPa以上，由于实验中各种复杂的因素导致实验数据比较分散，因此其实验结果不能用来标定理论数据。在QMD的计算中，由于铀的价电子数取14，并且铀是金属材料，导致高温下其能带数必须取得很大，计算量也相应地剧烈增大，因此要计算更高压强的Hugoniot点，需要花费大量的机时，不能指望用QMD方法计算一套完整的宽区状态方程，但QMD的计算结果可为状态方程建模提供参考。

4 结 论

采用基于密度泛函理论的第一原理方法，研究了铀的物态方程。基态计算结果表明：在低于100 GPa的压强下，α-U结构最稳定。 利用QMD方法，计算了有限温度下铀的物态方程，所得的300 K下铀的等温线在100 GPa压强范围内与实验结果符合得很好。在此基础上计算了铀的冲击Hugoniot点，并与实验数据以及QEOS结果进行了比较。结果表明：在100 GPa以下，QMD计算结果与实验结果符合得很好，而QEOS计算结果偏软。

[1] GANGULY J,KENNEDY G C.The melting temperature of uranium at high pressures [J].J Phys Chem Solids,1973,34(12):2272-2274.

[2] AKELLA J,SMITH G S,GROVER R,et al.Static EOS of uranium to 100 GPa pressure [J].High Pressure Res,1990,2(5/6):295-302.

[3] YOO C S,AKELLA J,MORIARTY J A.High-pressure melting temperatures of uranium:laser-heating experiments and theoretical calculations [J].Phys Rev B,1993,48(21):15529-15534.

[4] AKELLA J,WEIR S,WILLS J M,et al.Structural stability in uranium [J].J Phys Condens Matter,1997,9:L549-L555.

[5] YOO C S,CYNN H,SODERLIND P.Phase diagram of uranium at high pressures and temperatures [J].Phys Rev B,1998,57(17):10359-10362.

[6] WYCKOFF R W G.Crystal structures [M].New York:Interscience Publishers,1963:16.

[7] DEWAELE A,BOUCHET J,OCCELLI F,et al.Refinement of the equation of state ofα-uranium [J].Phys Rev B,2013,88(13):134202.

[8] MARSH S P.LASL shock Hugoniot data [M].Los Angeles,USA:University of California Press,1980.

[9] SKIDMORE I C,MORRIS E.Experimental equation-of-state data for uranium and its interpretation in the critical region [M]//Thermodynamics of nuclear materials.Vienna:International Atomic Energy Agency,1962:173-216.

[10] ISBELL W M,SHIPMAN F H,JONES A H.Hugoniot equation of state measurements for eleven materials to five megabars:AD721920 [R].Warren,Michigan:Materials & Structures Laboratory,1968.

[11] JONES M D,BOETTGER J C,ALBERS R C.Theoretical atomic volumes of the light actinides [J].Phys Rev B,2000,61(7):4644-4650.

[12] SODERLIND P,ERIKSSON O,JOHANSSON B,et al.Electronic properties off-electron metals using the generalized gradient approximation [J].Phys Rev B,1994,50(11):7291-7294.

[13] PENICAUD M.Calculated equilibrium properties,electronic structures and structural stabilities of Th,Pa,U,Np and Pu [J].J Phys Condens Matter,2000,12(27):5819-5829.

[14] SODERLIND P.First-principles elastic and structural properties of uranium metal [J].Phys Rev B,2002,66(8):085113.

[15] SODERLIND P,LANDA A,SADIGH B.First-principles elastic constants and phonons ofδ-Pu [J].Phys Rev B,2004,70(14):144103.

[16] HOOD R Q,YANG L H,MORIARTY J A.Quantum molecular dynamics simulations of uranium at high pressure and temperature [J].Phys Rev B,2008,78(2):024116.

[17] MORE R M,WARREN K H,YOUNG D A,et al.A new quotidian equation of state (QEOS) for hot dense matter [J].Phys Fluids,1988,31(10):3059-3078.