基于电流反馈模糊控制算法的光伏模拟器研究*

孟志强，邵　武，周华安，苏　烁

(1.湖南大学 电气与信息工程学院，湖南 长沙　410082；2.湖南大学 机械与运载工程学院，湖南 长沙　410082)



基于电流反馈模糊控制算法的光伏模拟器研究*

孟志强1†，邵武1，周华安2，苏烁1

(1.湖南大学 电气与信息工程学院，湖南 长沙410082；2.湖南大学 机械与运载工程学院，湖南 长沙410082)

摘要：设计与研究了一种基于BUCK直流变换器和电流反馈模糊控制算法的光伏电池阵列模拟器.该模拟器实时采集BUCK变换器输出电压并代入光伏电池工程数学模型，计算出电池电流作为模糊控制器的输入参考电流．该参考电流与BUCK变换器输出电流的差值及差值变化量作为模糊控制器的2个输入．模糊控制器通过模糊算法计算BUCK功率开关的导通占空比，使BUCK变换器的输出电压和电流准确对应于光伏电池V-I特性曲线的期望工作点，实现光伏特性模拟.模糊控制器使用三角形模糊隶属度函数，输入与输出变量的论域规范为[-3,3]，模糊规则49条.Matlab/Simulink仿真模型与试验系统的实验结果表明，模糊控制模拟器不仅能准确模拟光伏电池的静态输出特性，还能快速跟踪工作点变化或外部环境变化的光伏电池特性，超调量小于3.5%，稳态误差小于3.6%，纹波系数小于3%，跟踪时间约为0.3 s，能够为光伏发电系统的研究与开发提供优良的光伏阵列实验设备.

关键词：光伏阵列；模拟器；模糊控制；反馈；V-I特性曲线；BUCK直流变换器

光伏模拟器能够准确模拟任意光照和环境温度条件下光伏电池及其阵列的输出特性，且不受环境因素的影响．因此，在光伏发电系统的研究中被广泛用来替代光伏电池及阵列，以保证研发进度，降低研发成本，提高研发效率和保障结果的可信性[1-3].

目前光伏阵列模拟器的研究主要集中在以下3个方面：1)光伏电池工程数学模型,包括传统指数模型和平抛运动模型等[4-8]；2)主电路拓扑结构，采用不同的DC/DC拓扑结构和数字控制器实现光伏阵列模拟[9-11]；3)模拟器算法，传统模拟器算法主要有逐点逼近法、弦截法、迭代法和四折线法等[12-15].本文提出一种电流反馈模糊控制模拟器．该模拟器综合利用专家经验，设计简单，抗干扰能力强，响应速度快，对系统参数的变化有较强的鲁棒性 ，在光伏模拟器这种非线性系统中具有良好的控制效果，能够极大地弥补传统控制方法的不足[16-18].

模糊控制光伏模拟器主电路采用BUCK变换器，控制器为TMS320F2812，模糊控制生成BUCK主电路的PWM控制量，使变换器的输出工作点位于光伏电池V-I曲线上，实现光伏模拟.Matlab/Simulink仿真和样机实验结果一致性好，模拟器能够快速稳定地追踪参考工作点，实现各种条件下完整V-I特性曲线的模拟，且超调量小于3.5%，稳态误差小于3.6%，纹波系数小于3%，跟踪时间小于0.3 s.

1光伏电池输出特性及工程数学模型

1.1光伏电池输出特性

光伏电池模拟器的主要目标是实现对光伏电池输出V-I特性曲线的模拟.光伏电池输出特性具有非线性，受光照强度和环境温度的影响大，如图1所示．当光照强度S一定、环境温度T升高时，输出电流I增大，输出电压V下降；当环境温度T一定、光照强度S升高时，输出电流I增大，输出电压V也增大.

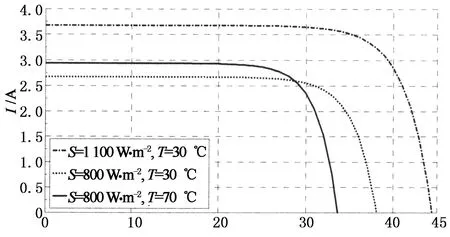
V/V

1.2光伏电池工程数学模型

描述光伏电池输出特性的简化数学模型[19]一般使用标准测试条件(光照强度Sref=1 000 W/m2，环境温度Tref=25 ℃)时的短路电流Isc，开路电压Voc，最大功率点电流Im与最大功率点电压Vm:

(1)

(2)

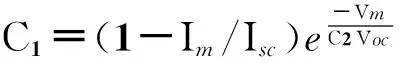
(3)

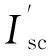
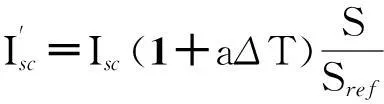
(4)

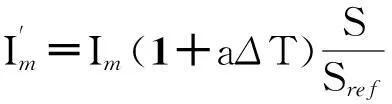
(5)

(6)

(7)

式中：a=0.002 5/℃；b=0.5；c=0.002 88/℃.

2模糊控制

2.1模拟器的目的

当光照强度和温度不变时，光伏电池的V-I特性曲线是唯一确定的.对于确定的负载，负载的V-I曲线必与光伏电池V-I曲线交于一确定点C.模拟器的控制目标就是通过控制DC/DC电路的占空比d，使负载运行于光伏电池V-I特性曲线上的确定点，如图2所示的C点，假定负载为R1.

图2　模拟器控制目标

2.2模糊控制器的工作原理

光伏模拟器工作原理的结构如图3所示．图3中虚线左侧为模糊控制器，模糊控制器由TMS320F2812高性能嵌入式单片机实现，右侧为基于BUCK电路的DC/DC变换器.模糊控制器的输入为模拟器输出电流In与光伏电池模型输出电流Ire的差值e(n)及差值变化量ec(n)，输出为BUCK电路开关占空比D(n).图3中，Vn和In分别为模拟器中BUCK电路的输出电压和电流；TMS320F2812实时采集Vn，用光伏电池工程数学模型计算出模糊控制器的输入参考电流Ire，Ire与n时刻的In比较，得到电流差值e(n)；e(n-1)为n-1采样时刻的电流差值，如图2中A和B点所示；E(n)和Ec(n)分别为n时刻e(n)和ec(n)经Ke和Kec量化的结果，作为模糊控制算法的输入；A(n)为模糊控制输出的占空比增量，经Ka量化后得到实际占空比增量a(n)，a(n)与当前占空比D(n-1)求和得到新的占空比D(n)，控制BUCK电路使其输出工作点运行于光伏电池V-I特性曲线上，实现电流反馈光伏模拟.Ka使系统以合适的占空比变化步长进行调整.

图3中阈值处理环节为三段非线性环节，具有两个重要功能.一是限幅滤波，当e或ec大于设定值Xmax时,输出限幅为Ymax，滤除干扰影响；二是限幅控制，当e或ec小于设定值Xmin时,输出钳制为0，使控制器的输出占空比D(n)保持不变.

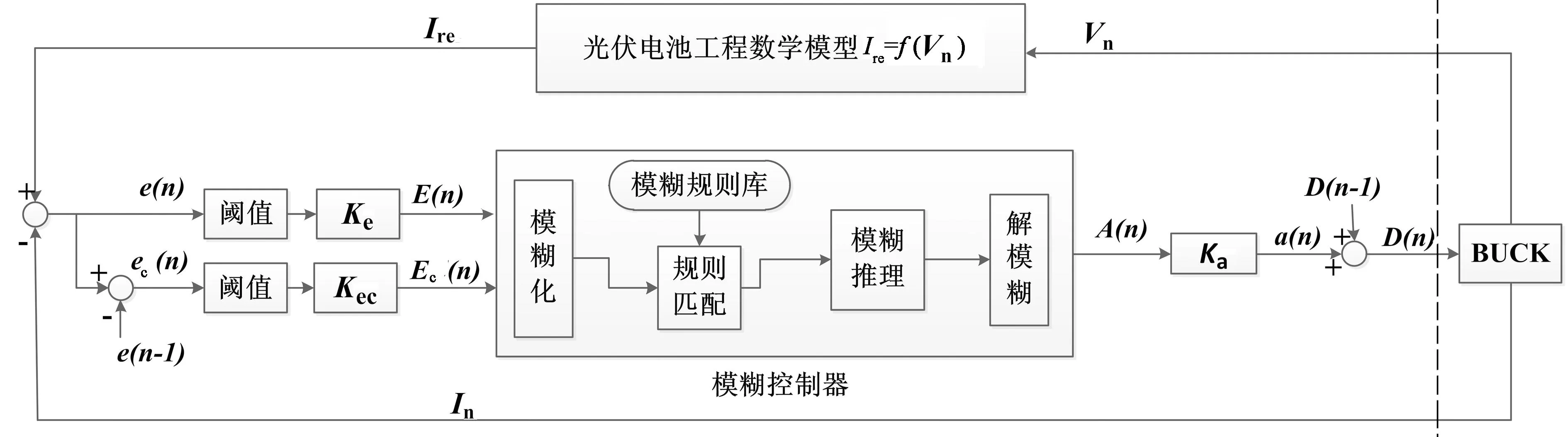
图3　模糊控制结构图

2.3模糊算法设计

模糊控制器输入输出变量[(E(n),Ec(n)，A(n)]的论域均被规范化为{-3，-2，-1，0，1，2，3}，隶属度函数采用幅值为1的等腰三角函数，如图4所示．图中{NB，NM，NS，ZO，PS，PM，PB}为模糊子集，分别对应“负大、负中、负小、零、正小、正中、正大”.

综合光伏电池特性和模拟器控制目标，模糊算法规则遵循以下3条基本原则：

1)e为正.若ec不变或为正，则占空比增量a方向为正，步长较大；反之，a方向为正，步长较小；

2)e为负.若ec不变或为负，则a方向为负，步长较大；反之，a方向为负，步长较小；

3)若e和ec在所设阈值内，则a为0，占空比D(n)=D(n-1)不变.

图4　模糊输入输出隶属函数

可推出如下模糊规则：

IFE(n)=PB andEc(n)=NB，THENA(n)=ZO；

IFE(n)=PB andEc(n)=NM，THENA(n)=PS；

……

得出的49条控制器模糊规则如表1所示，可形成图3中的模糊规则库.模糊控制器在完成模糊推理后，采用重心法解模糊[11]获得精确控制量A(n).

表1　模糊规则表

3模拟器及测试电路主参数

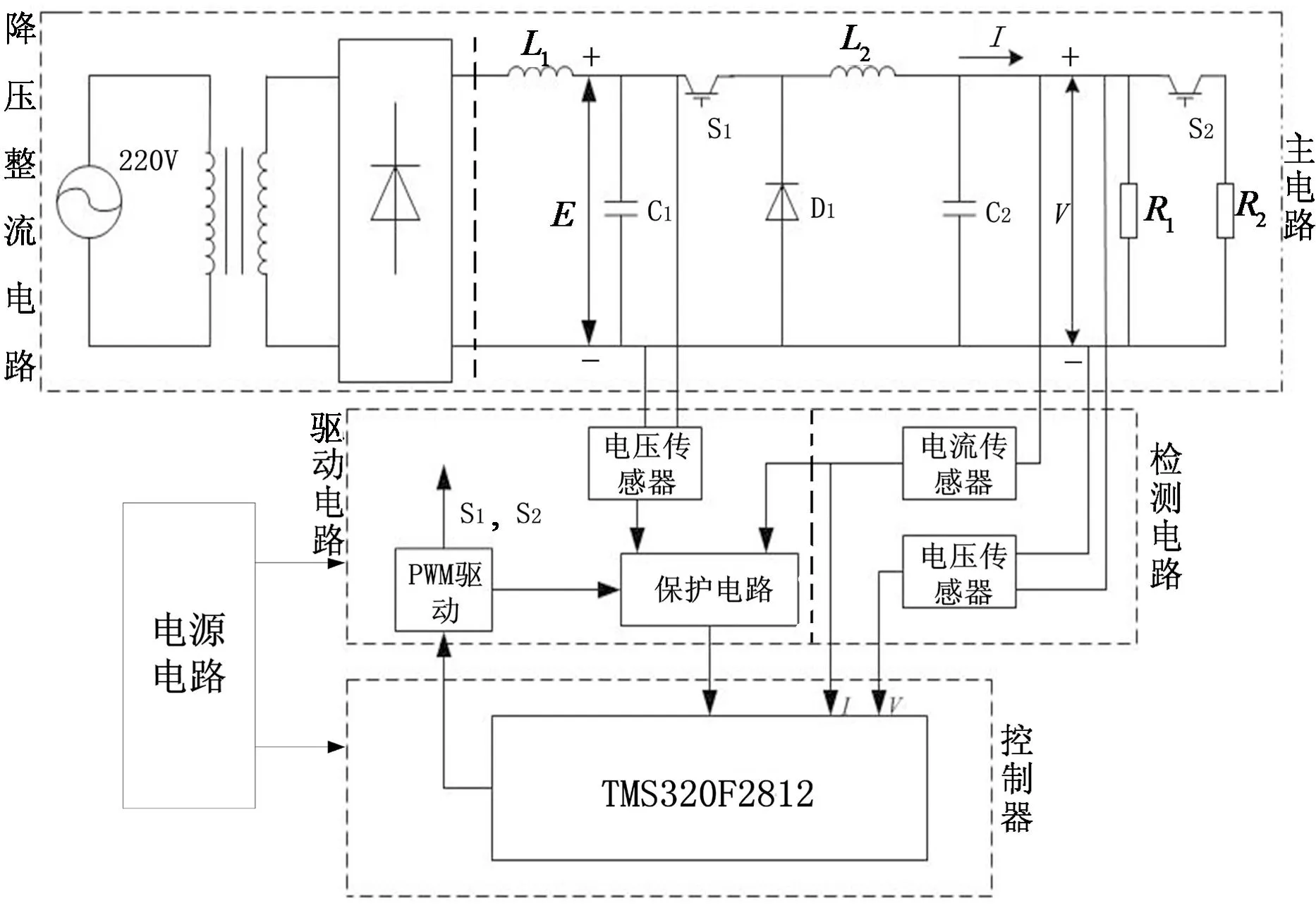
(a)原理电路图

(b)硬件实验平台

4实验与分析

在图6所示模糊控制模拟器仿真模型和图5(b)所示模拟器实验系统上，对不同环境条件下的模拟器性能进行了验证.仿真模型由BUCK主电路、光伏电池数学模型、模糊控制器以及PWM发生器组成，图6中的Stepi(i=1,2,3,4)模块用来控制负载、光照和温度的突变.

4.1仿真实验

仿真分为启动与工作点突变跟踪、光照量突变跟踪和温度突变跟踪3种情况.所有仿真均从光伏电池的短路电流开始.

4.1.1启动与工作点突变跟踪

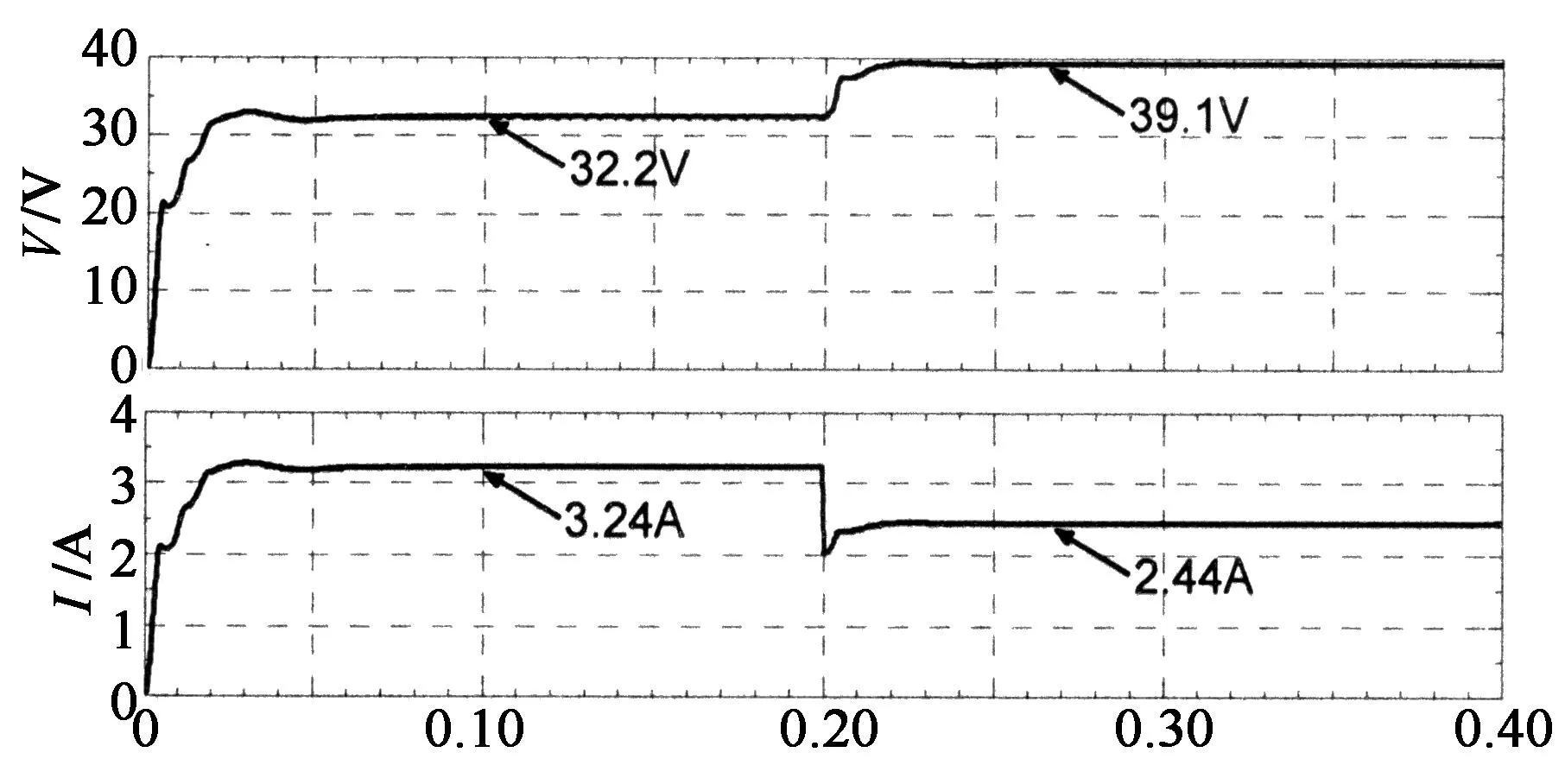
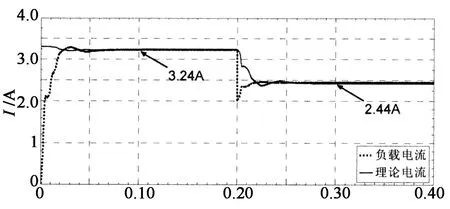
本实验研究标准测试条件下模拟器的启动性能和工作点突变跟踪性能.图7为初始工作点负载R=10 Ω时系统启动与t=0.2 s时R突变为16 Ω的跟踪仿真波形，图8为初始工作点负载R=16 Ω时系统启动与t=0.2 s时R突变为10 Ω的跟踪仿真波形.其中，图7(a)和图8(a)的上图均为负载电压波形，下图为负载电流波形；图7(b)和图8(b)均为对应的负载电流和光伏电池理论电流波形.

图6　光伏模拟器仿真模型

t/s

t/s

由光伏电池的V-I特性曲线(图2)可知，当模拟器负载R小时，其输出电压小、电流大；反之，负载R大时，输出电压大、电流小.由模拟器工作原理和控制算法可知，基于电流反馈的模糊控制模拟器的动态特性跟实际负载电流与目标工作点电流的差值有关，差值越大调节时间越长.

图7中的初始工作点负载比图8中的小，系统启动跟踪到稳态的时间约为0.07 s，图8的时间约为0.05 s；在0.2 s时进行工作点突变跟踪，图7的跟踪时间约为0.04 s，图8的跟踪时间约为0.1 s；2种情况的稳态误差都约为0.8%，纹波系数约为0.6%.

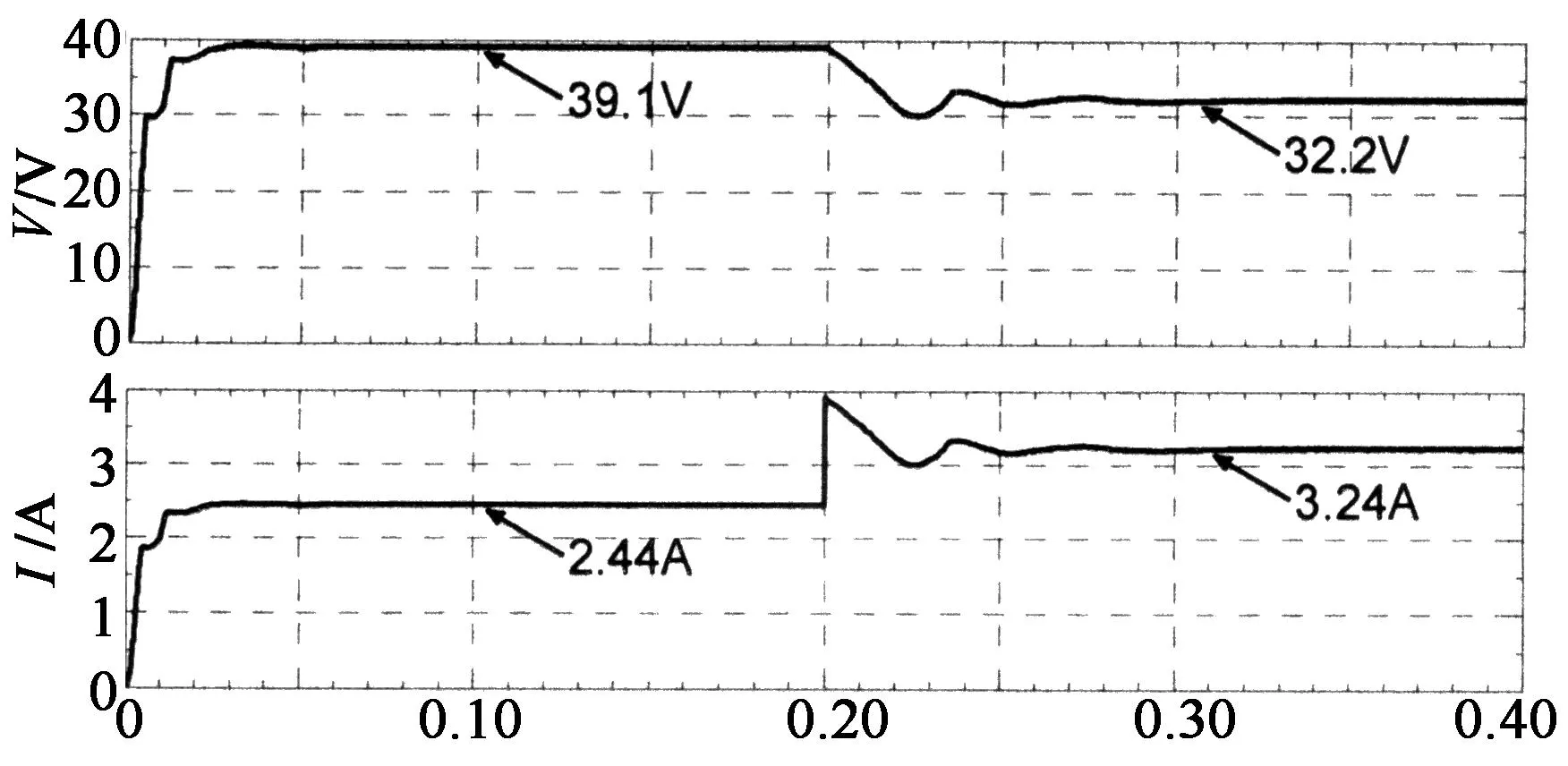
t/s

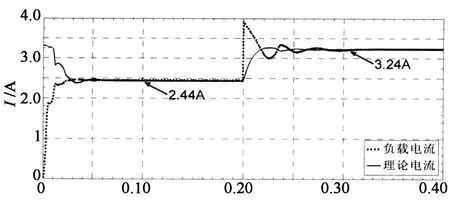
t/s

4.1.2光照强度突变跟踪

本实验研究环境温度T=30 ℃，负载R=10 Ω条件下，光照强度S在0.2 s时从1 000 W/m2突变为800 W/m2的模拟器跟踪性能.仿真波形如图9所示，图9(a)上图和下图分别为负载电压与电流波形，图9(b)为对应的负载电流和光伏电池理论电流波形.模拟器完成跟踪的时间约为0.12 s，稳态误差和纹波系数分别为0.8%和0.6%.同时，从仿真结果可以清楚地看出，光照量下降对光伏电池V-I特性的影响：目标工作点电压和电流都会降低.

t/s

t/s

4.1.3温度突变跟踪

本实验研究光照强度S=1 000 W/m2，负载R=8 Ω条件下，环境温度T在0.2 s时从70 ℃突变为10 ℃的模拟器跟踪性能.仿真波形如图10所示，图10(a)上图与下图分别为负载电压与电流波形，图10(b)为对应的负载电流和光伏电池理论电流波形.模拟器完成跟踪的时间约为0.08 s，稳态误差和纹波系数分别为1% 和0.6%.

从仿真结果还可以看出，在较小的负载(如R=8 Ω)条件下，环境温度下降对光伏电池V-I特性的影响：目标工作点电压和电流都会降低；反之，若负载较大，目标工作点电压与电流都会升高.

4.2模糊算法与逐点逼近法的对比实验

在图5所示的光伏模拟器系统中，分别用本文模糊算法和逐点逼近法对模拟器启动、工作点突变跟踪、环境突变跟踪进行了实验研究.实验波形均由泰克DPO2012B双踪数字示波器采集，负载电流的采样电阻为0.1 Ω.

t/s

t/s

4.2.1启动实验

本实验检验光照强度S=1 100 W/m2，温度T=30 ℃，负载R=10 Ω时，采用模糊算法与逐点逼近法的模拟器启动性能.实验波形分别如图11(a)和图11(b)所示.模糊算法启动跟踪的时间约为0.2 s，稳态误差约为2%，纹波系数约为2.8%；逐点逼近法启动跟踪的时间约为0.26 s，稳态误差约为3%，纹波系数约为3%.显然，模糊算法的启动跟踪速度快于逐点逼近法，稳态误差更小.

4.2.2工作点突变跟踪实验

本实验研究模拟器在光照强度S=1 100 W/m2，温度T=30 ℃时，采用模糊算法与逐点逼近法的工作点突变跟踪性能.图12和图13分别为模糊算法与逐点逼近法的实验波形，其中图12(a)和图13(a)均为负载R=8 Ω突变为R=16 Ω的实验波形，图12(b)和图13(b)均为负载R=16 Ω突变为R=8 Ω的实验波形.

由图12和图13可知，初始工作点不同，追踪时间存在差异.图12(a)的初始工作点负载比图12(b)的小，跟踪时间约为0.18 s，而图12(b)的跟踪时间约为0.32 s，稳态误差均为2.2%；图13(a)的跟踪时间约为0.2 s，而图13(b)的跟踪时间约为0.38 s，稳态误差均为2.6%.显然，模糊算法的跟踪速度明显快于逐点逼近法，稳态误差更小.

(a)模糊算法启动实验波形

(b) 逐点逼近法启动实验波形

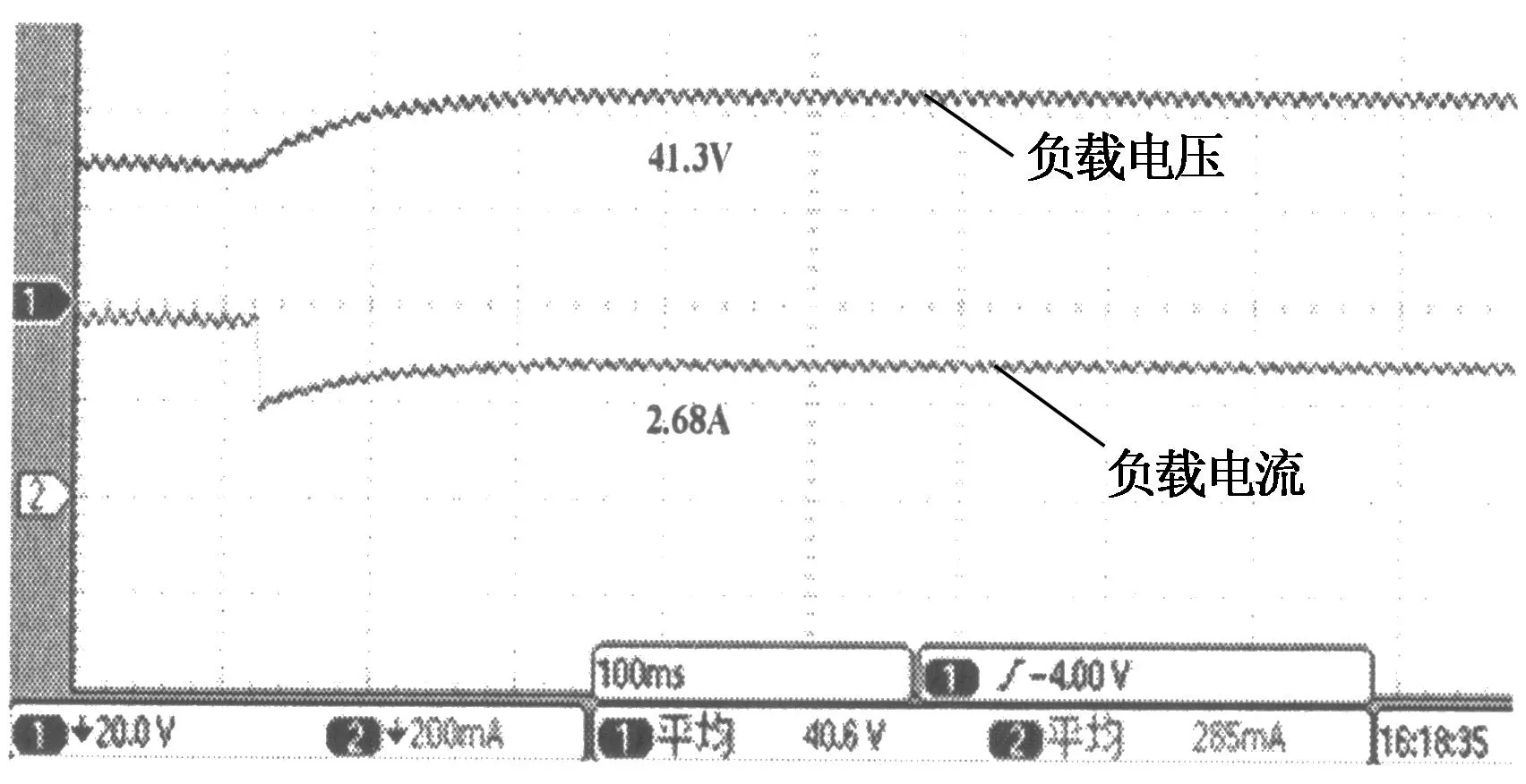
(a)初始工作点负载R=8 Ω的实验波形

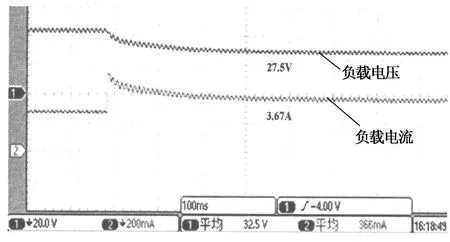
(b)初始工作点负载R=16 Ω的实验波形

4.2.3环境突变跟踪实验

本实验研究采用模糊算法和逐点逼近法的模拟器对环境突变的跟踪性能.

图14(a)和图14(b)分别为模糊算法与逐点逼近法在环境温度T=30 ℃，负载R=11 Ω条件下，光照强度从1 200 W/m2突变为800 W/m2时的实验波形.图14(a)的跟踪时间约为0.11 s，稳态误差约为2.2%；图14(b)的跟踪时间约为0.2 s，稳态误差约为3%.

(a)初始工作点负载R=8 Ω的实验波形

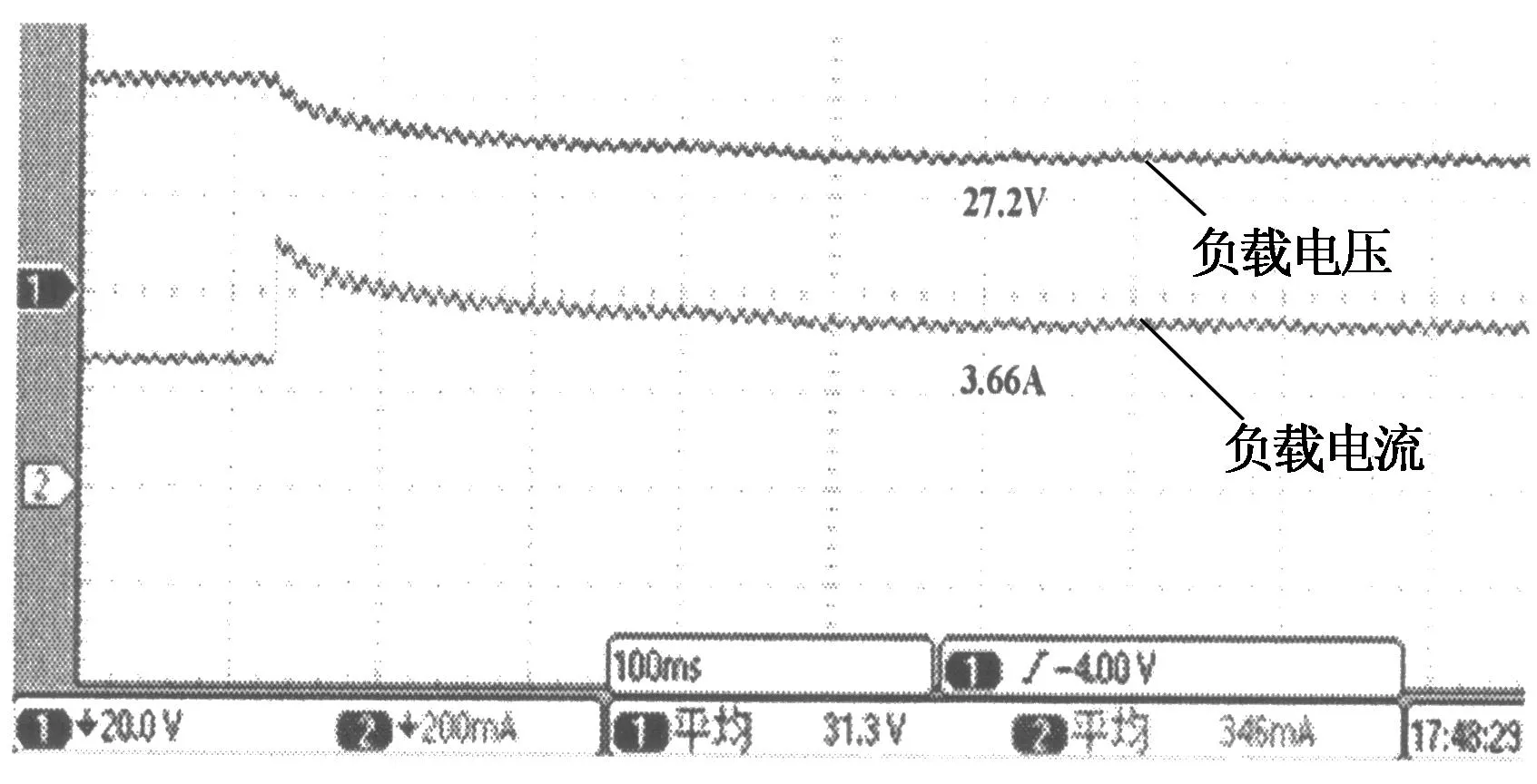
(b)初始工作点负载R=16 Ω的实验波形

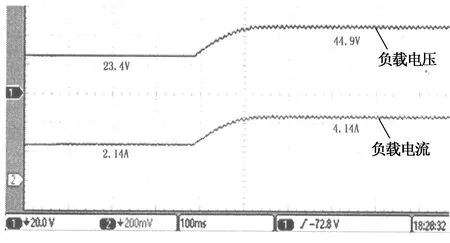
(a)模糊算法光照量突变跟踪实验波形

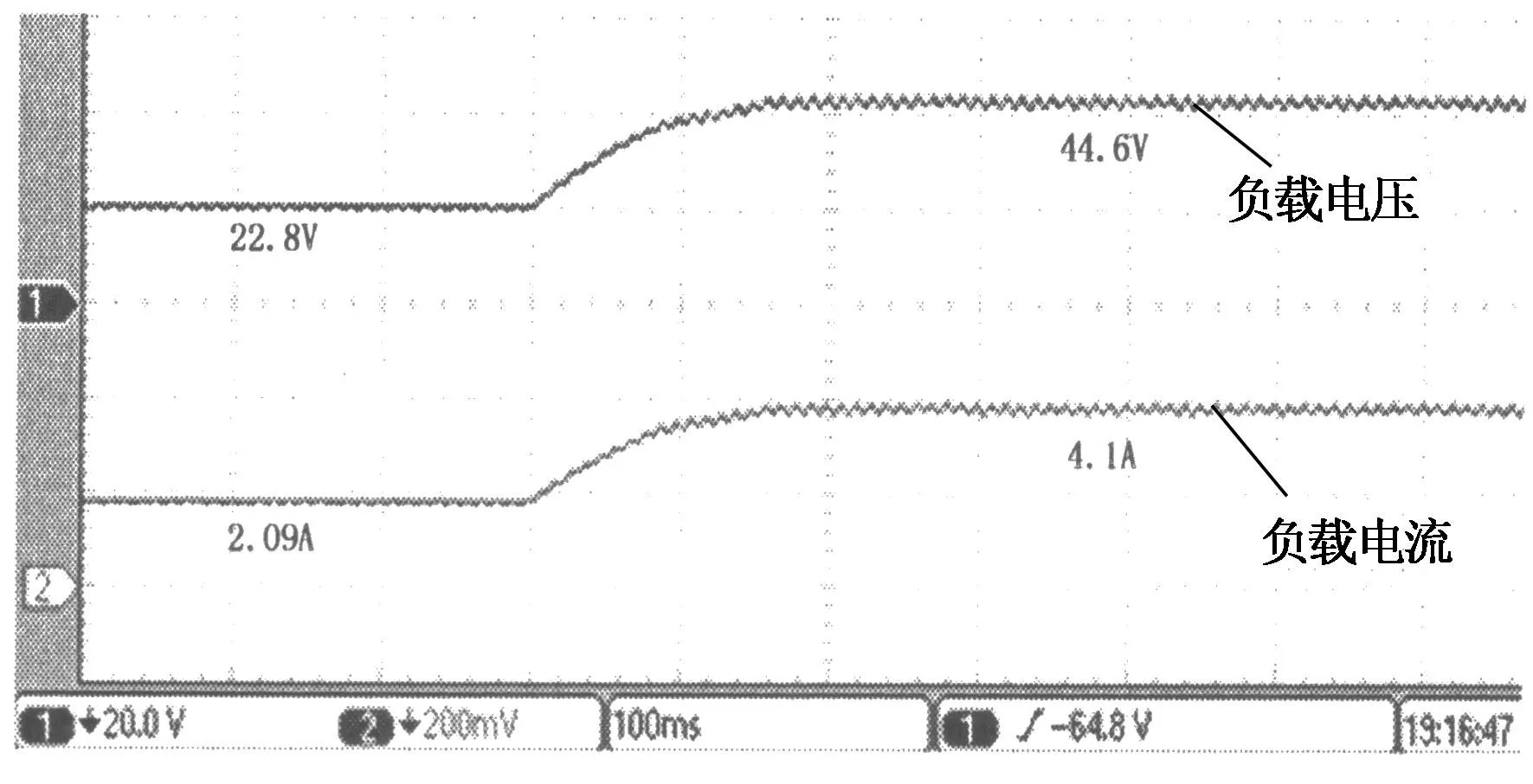
(b)逐点逼近法光照量突变跟踪实验波形

图15(a)和图15(b)分别为模糊算法与逐点逼近法在光照强度S=1 100 W/m2，负载R=6 Ω条件下，温度从30 ℃突变为70 ℃时的实验波形.图15(a)的跟踪时间约为0.12 s，稳态误差约为2.2%；图15(b)的跟踪时间约为0.3 s，稳态误差约为3.2%.

可见，模糊算法具有比逐点逼近法更快的跟踪速度和更小的稳态误差.

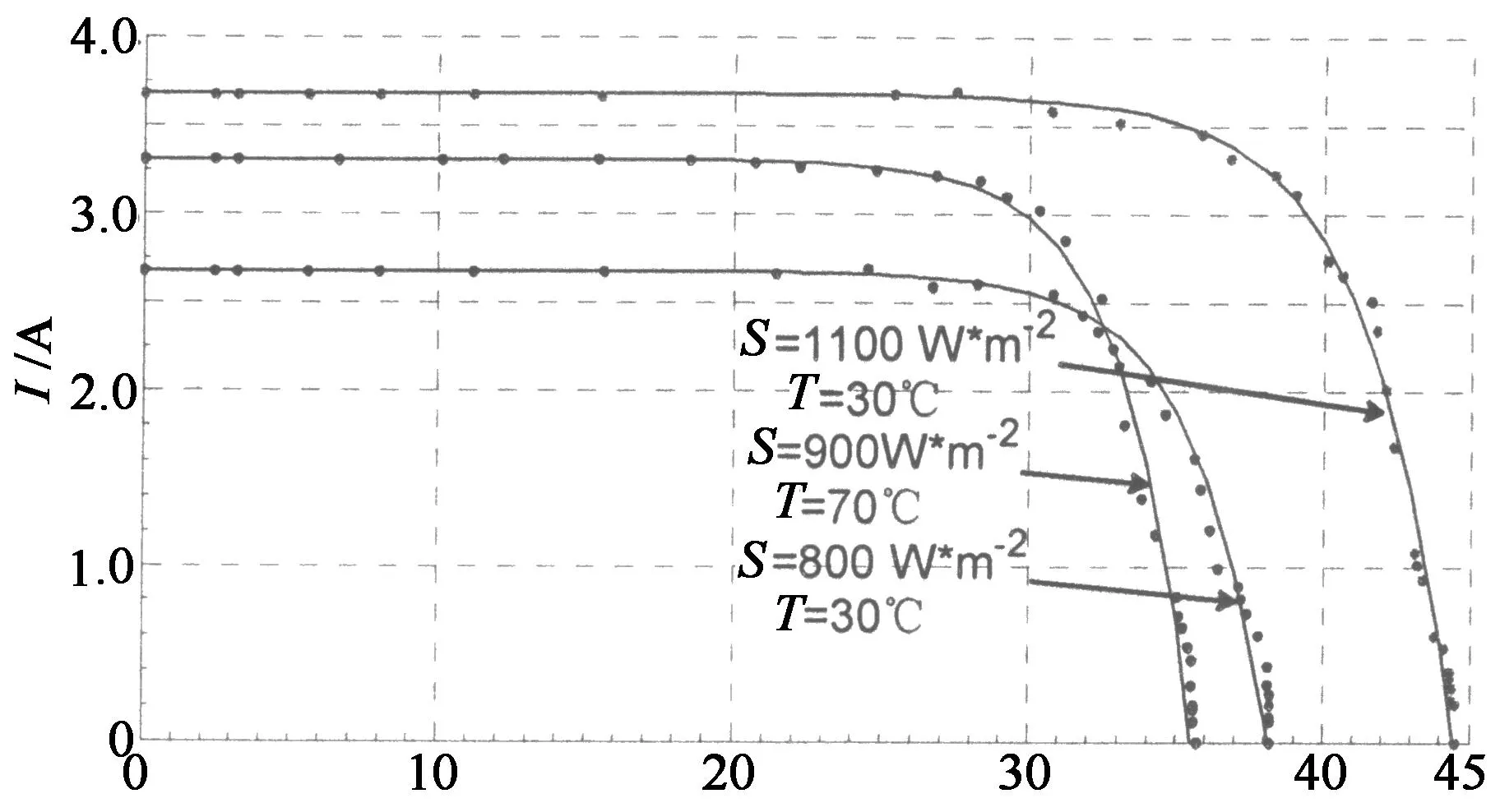
4.3不同条件下模糊算法模拟器的完全V-I特性实验

本实验完成了3种不同环境条件：①S=1 100 W/m2，T=30 ℃；②S=800 W/m2，T=30 ℃；③S=900 W/m2，T=70 ℃时模糊控制模拟器对光伏电池V-I特性的模拟性能研究.

实验通过模糊控制算法调节BUCK电路主开关的导通占空比d，取流过负载电阻的电流和负载电阻的端电压作为试验数据.试验中,对每一种条件都取20～30组试验数据,对应负载电阻位于[0,200 Ω]区间.将试验数据标注于相应环境条件的光伏电池V-I理论曲线上，如图16所示.由图16可知，在3种不同环境条件下，模拟器均能很好地实现光伏V-I曲线模拟.图中误差的均方差可忽略不计，其绝对值可认为是由模糊算法阈值、采样电阻精度和模拟负载的滑线电阻发热等因素产生的.

(a)模糊算法温度突变跟踪实验波形

(b)逐点逼近法温度突变跟踪实验波形

V/V

5结论

本文提出了一种电流反馈型光伏模拟器模糊控制算法，采用BUCK主电路和TMS320F2812控制芯片设计了模糊控制模拟器实验平台.该算法实时采集模拟器输出电压和电流，将输出电压代入光伏电池工程数学模型计算参考电流，参考电流与输出电流比较，其差值及差值变化量作为模糊控制器的输入，模糊控制器输出用于产生BUCK开关的PWM控制信号，从而使模拟器输出工作点逼近目标点，实现对光伏电池阵列输出V-I特性的模拟.仿真实验和模拟器样机的模糊算法与逐点逼近法对比实验结果表明：电流反馈模糊控制算法能够实现不同条件下光伏电池特性曲线的完全模拟，且模拟性能远优于逐点逼近法，具有动态响应速度快和模拟精度高等特点，在光伏电池阵列模拟器系统和光伏发电系统的研究与开发中具有极大的实用价值.

参考文献

[1]WANG Kui, LI Yong-dong, RAO Jian-ye,etal. Design and implementation of a solar array simulator[C]//Proceedings of International Conference on Electrical Machines and Systems. New York: IEEE, 2008:2633-2636.

[2]ZHU Wen-hua, YANG Shan-shui, WANG Li,etal. Modeling and analysis of output features of the solar cells based on Matlab/Simulink[C]//Proceedings of International Conference on Materials for Renewable Energy and Environment. New York: IEEE,2011:730-734.

[3]赵剑飞，姜建国.智能太阳能模拟系统的研究[J].太阳能学报, 2012, 33(1):18 -23.

ZHAO Jian-fei, JIANG Jian-guo. Study on the intelligent solar cells simulation system[J]. Acta Energiae Solaris Sinica, 2012,33(1):18-23. (In Chinese)

[4]傅望,周林.光伏电池工程用数学模型[J].电工技术学报,2011,26(10): 211-216.

FU Wang, ZHOU Lin. Research on engineering analytical model of solar cells [J].Transactions of China Electrotechnical Society, 2011, 26(10):211-216.(In Chinese)

[5]田琦,赵争鸣,韩晓艳. 光伏电池模型的参数灵敏度分析和参数提取方法[J].电力设备自动化,2013,33(5):119-124.

TIAN Qi, ZHAO Zheng-ming, HAN Xiao-yan. Sensitivity analysis and parameter extraction of photovoltaic cell model[J]. Electric Power Automation Equipment, 2013,33(5): 119-124. (In Chinese)

[6]ZHOU Jian-liang, WANG Bing, ZHANG Yi-ming. Parameter identification and output power prediction of photovoltaic array based on the measured data[J]. Renewable Energy Resources, 2012, 30(7): 1-4.

[7]杨永恒,周克亮. 光伏电池建模及 MPPT 控制策略[J]. 电工技术学报,2011,26(1):229-234.

YANG Yong-heng, ZHOU Ke-liang. Photovoltaic cell modeling and MPPT control strategies[J]. Transactions of China Electrotechnical Society,2011, 26(1): 229-234.(In Chinese)

[8]程泽,董梦男,杨添剀, 等.基于自适应混沌粒子群算法的光伏电池模型参数辨识[J]. 电工技术学报, 2014, 29(9): 245-252.

CHENG Ze, DONG Meng-nan, YANG Tian-kai,etal. Extraction of solar cell model parameters based on self-adaptive chaos particle swarm optimization algorithm[J]. Transactions of China Electrotechnical Society, 2014,29(9): 245-252. (In Chinese)

[9]王付胜,文家燕, 张兴,等.数字式光伏阵列模拟器[J].太阳能学报,2012,33(3):494-499.

WANG Fu-sheng, WEN Jia-yan, ZHANG Xing,etal. An investigation on digital photovoltaic array simulator[J]. Acta Energiae Solaris Sinica , 2012,33(3):494-499. (In Chinese)

[10]YAZDANI A, DASH P P. A control methodology and characterization of dynamics for a photovoltaic system interfaced with a distribution network[J]. IEEE Transactions on Power Delivery, 2009, 24(3):1538-1551.

[11]DAS N, ALGHADEER A, ISLAM S. Modelling and analysis of multi-junction solar cells to improve the conversion efficiency of photovoltaic systems[C]//Proceedings of 2014 Australasian Universities Power Engineering Conference. New York: IEEE, 2014:1-5.

[12]周华安,王海鸥,孟志强,等.基于TMS320F2812和BUCK电路的光伏阵列模拟器[J].湖南大学学报：自然科学版,2013, 40(9): 42-47.

ZHOU Hua-an, WANG Hai-ou, MENG Zhi-qiang,etal. A new kind of photovoltaic array simulator based on TMS320F2812 DSP and BUCK circuit[J]. Journal of Hunan University：Natural Sciences, 2013,40(9):42-47. (In Chinese)

[13]NOCERINO J C, LIU S H. Solar simulator air mass zero calibration method[C]//Proceedings of 2010 35th IEEE Photovoltaic Specialists Conference. New York: IEEE, 2010: 2590-2593.

[14]ZHANG Hou-sheng, ZHAO Yan-lei. Research on a novel digital photovoltaic array simulator[C]//Proceedings of 2010 International Conference on Intelligent Computation Technology and Automation. New York: IEEE, 2010: 1077-1080.

[15]QI Hui, BI Yan-lei, YAN Wu. Development of a photovoltaic array simulator based on buck convertor[C]//Proceedings of 2014 International Conference on Information Science, Electronics and Electrical Engineering. New York :IEEE, 2014:14-17．

[16]ZENG Guo-hui, LIU Qi-zhong. An intelligent fuzzy method for MPPT of photovoltaic arrays[C]//Proceedings of Second International Symposium on Computational Intelligence and Design. New York: IEEE, 2009:356-359.

[17]FENG Gang. A survey on analysis and design of model-based fuzzy control systems[J]. IEEE Transactions on Fuzzy Systems, 2006,14(5):676-697.

[18]CHENG Ze, PANG Zhi-chao, LIU yan-li,etal. An adaptive solar photovoltaic array reconfiguration method based on fuzzy control[C]//Proceedings of 2010 8th World Congress on Intelligent Control and Automation. New York: IEEE, 2010:176-181.

[19]苏建徽,余世杰.硅太阳能电池工程用数学模型[J].太阳能学报,2001,22(4):409-412.

SU Jian-hui, YU Shi-jie. Silicon solar cell mathematical models[J]. Acta Energiae Solaris Sinica, 2001, 22(4) : 409-412. (In Chinese)

A New Photovoltaic Array Simulator Based on Current Feedback Fuzzy Control

MENG Zhi-qiang1†,SHAO Wu1,ZHOU Hua-an2,SU Shuo1

(1. College of Electrical and Information Engineering, Hunan Univ, Changsha,Hunan410082, China;2. College of Mechanical and Vehicle Engineering, Hunan Univ, Changsha, Hunan410082, China)

Abstract:A new photovoltaic array simulator was studied and designed on the basis of a Buck DC converter and the current feedback fuzzy control theory. The output voltage of the Buck converter was measured and used to calculate the current of photovoltaic array engineering mathematics model used as the input reference current of the fuzzy controller. The difference of the reference current and the real-time feedback current of the Buck converter and its rate of change were regarded as two input variables of the fuzzy controller, and then, the duty cycle of the electronic power switch was adjusted with closed-loop fuzzy algorithm to make the output voltage and the current of the simulator work at the anticipant point of the photovoltaic array on the V-I characteristic curve and realize the simulation of photovoltaic properties. A fuzzy controller with TMS320F2812CPU and a triangular fuzzy membership function was used and the domain of the input and output variables limited to [-3 3] contained 49 fuzzy rules. Simulation and experiment results have shown that the fuzzy control simulator can not only accurately simulate the static output characteristics of the photovoltaic cell, but can also rapidly realize the dynamic characteristics when the load or the external environment changes, and the approximate error is under 3.6%, the overshoot under 3.5%, the ripple coefficient under 3% and the tracking time about 0.3s. The fuzzy control simulator can work well as PV array experiment equipment for the research and development of photovoltaic systems.

Key words:photovoltaic array；simulator; fuzzy control; feedback; V-I characteristic curve；Buck DC converter

中图分类号：TM615

文献标识码：A

作者简介：孟志强(1964-)，男，湖南益阳人，湖南大学教授，博士生导师†通讯联系人，E-mail: mengzhiqiang@126.com

基金项目：国家自然科学基金资助项目(51207026,51377049), National Natural Science Foundation of China(51207026,51377049)

*收稿日期：2015-04-10

文章编号：1674-2974(2016)02-0092-09