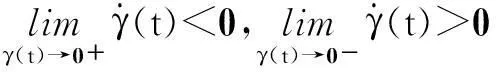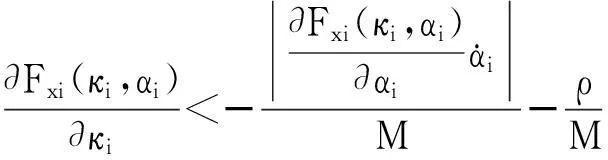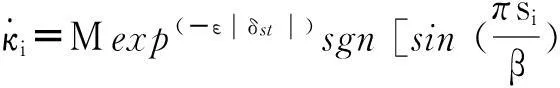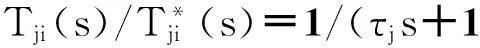分布式电驱动汽车AFS与电液复合制动集成控制*

袁希文，文桂林，周　兵

(湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙　410082)



分布式电驱动汽车AFS与电液复合制动集成控制*

袁希文†，文桂林，周兵

(湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙410082)

摘要：针对分布式电驱动汽车，以实现车辆主动安全性同时兼顾制动能量回收为目标，提出一种主动前轮转向(AFS)与电液复合制动集成的控制策略.AFS控制器采用滑模变结构控制，滑移率控制器采用滑模极值搜索算法，基于分层结构(上层为期望制动力矩计算模块，中层为考虑执行器带宽的动态控制分配模块，下层为电机与液压复合执行器)，并考虑位置与速率约束.转向制动时，考虑车辆纵向动力学对侧向动力学的影响，引入前轮转角对滑移率控制律进行了修正.在MATLAB/Simulink中建立七自由度整车模型，对控制算法进行了验证.结果表明：分离路面直线制动时，所提出的控制策略可以同时保证制动能量回收和制动方向稳定性；转弯制动时，可以更好地跟踪理想横摆角速度，提高了车辆的侧向稳定性.

关键词：车辆工程；电液复合制动；主动前轮转向；能量回收；控制策略；极值搜索算法

分布式电驱动汽车因其诸多优点而受到工业界和学者们的青睐[1-2]．电动车在复杂路面条件下的制动力矩分配直接影响车辆的稳定性，车轮突然滑转或抱死会引起侧向附着降低，严重时可导致车辆失去转向能力甚至甩尾.传统的产品化的ESP控制利用ABS和ASR控制作为下层来控制车轮的滑移(转)率，但现有的分布式驱动电动汽车制动力矩分配控制未能实现与ABS和ASR控制的结合[3]，因此，如何设计适合分布式驱动电动车的滑移率控制器，提高制动效能，同时保证车辆主动安全性是需要关注的一个问题.

电动车具有电机制动响应快、实时性好、精准可控的优点，但其最大制动力矩受限于电机本身特性和电池荷电状态(SoC)，无法满足一些强制动工况的需求，故电动车常采用电机再生制动和液压制动的复合制动方式[4].电液复合制动技术也被认为是提高电动车续航和车辆主动安全性的关键技术．目前对电液扭矩协调的研究主要采用未包含执行器动力学的静态分配方法[5]，然而由于二者执行带宽的差异，会使实际响应力矩的复合效果与期望值之间有偏差.因此，如何在考虑执行器动力学条件下设计动态控制分配是需要关注的又一问题.鉴于此，本文提出一种分离路面下AFS与电液复合制动集成的控制策略.AFS用来补偿侧向稳定性，采用滑模控制.电液复合制动用来实现滑移率控制，采用滑模极值搜索算法，并考虑转弯制动时纵向动力学对侧向动力学的影响，引入前轮转角对滑移率控制律进行修正，进一步提高车辆侧向稳定性.针对电液复合制动，采用动态控制分配法协调电机与液压制动力矩，通过增加对执行机构速率的惩罚，扩展一般的二次规划控制分配算法，使算法具有频率依赖的特性，实现对执行机构带宽的考虑.最后对控制策略进行仿真验证.

1车辆动力学模型

面向控制器验证用车辆模型采用七自由度整车模型，如图1所示.

图1　七自由度整车模型

其中七自由度包含整车纵向、侧向、横摆3个自由度和4个车轮旋转自由度.整车纵向、横摆、侧向动力学方程表达式见式(1).

(1)

式中：m为整车质量；vx为纵向速度；vy为侧向速度；r为横摆角速度；Izz为整车绕z轴的转动惯量；Fxi,Fyi分别为轮胎纵向力和侧向力，其中i=fl,fr,rl,rr，分别为左前轮、右前轮、左后轮、右后轮；g为重力加速度；a,b分别为前轴、后轴至质心距离；Tf,Tr分别为前、后轮距；δl,δr分别为左、右前轮转角.车轮采用魔术公式轮胎模型.

2 控制策略

控制策略采用内外环结构.为提高车辆系统对参数不确定性的鲁棒性，外环AFS控制器采用滑模控制，内环滑移率控制器采用滑模极值搜索算法.针对目前复合制动电液制动力矩协调难的特点，利用考虑执行器带宽的动态控制分配法进行电机与液压制动力矩协调，并采用分层控制结构，实现控制问题的解耦化、简易化，如图2所示.如上层滑移率控制器保证不出现抱死拖滑，得到总期望制动力矩即可，无需考虑电机与液压是如何协调的；中层控制分配模块只需在考虑执行器动力学条件下，实现对总期望制动力矩的分配即可；下层电机与液压执行器仅需考虑约束条件下执行控制分配模块给出的分配值即可，无需考虑分配值是如何得到的.

图2　集成控制策略框图

2.1AFS控制器

滑模控制器设计基于线性二自由度模型[6]:

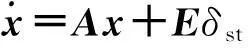
(2)

式中：Cf0,Cr0分别为前后轴轮胎等效侧偏刚度；δst为驾驶员输入的前轮转角.

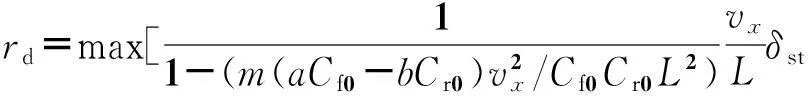
μ(g/vx)].

(3)

选择切换函数为

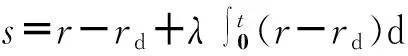
(4)

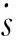
(5)

式中：a21,a22和e2分别为矩阵A和E的元素.

为了使系统存在扰动和参数不确定性时仍能保证滑模条件，定义如下控制律：

ulaw=ueq-Krsgn (s).

(6)

式中：sgn为符号函数；增益Kr为控制器设计参数，决定了系统达到滑模面的速度.该控制增益应选择较大值以满足滑模可达条件：

(7)

此外，为了进一步消除控制输入的高频抖振，用饱和函数替代符号函数sgn (s)，即

(8)

因此，最终滑模控制律为：

δf=ulaw=ueq-Krsat(s/ψ).

(9)

式中：ψ为边界层厚度，本文取0.05.

上述控制律得到的是前轮输入转角，车轮附加转角为

δc=δf-δst.

(10)

2.2滑移率控制器(WSC)

参考滑移率随路面条件变化而不断变化，若设定为常值，变路面条件下控制效果将变差.本文采用滑模极值搜索算法实现滑移率控制，它通过不断搜寻轮胎纵向力-滑移率曲线的极值点，自适应路面条件变化，是一种不依赖参考滑移率的控制方法[7].

设计滑移率控制器首先需要选择合适的切换函数，下面构造滑模面为[8]：

si=Fxi(κi,αi)-ρ t.

(11)

为了简化控制律，构造滑模面时没有考虑轮胎垂直载荷对Fxi的影响.但轮胎模型中考虑了垂直载荷对Fxi的影响，因此，控制器在搜寻最优滑移率的过程中仍涉及了垂直载荷变化因素，不影响最优滑移率的搜寻.

将si对时间求导得出

(12)

(13)

式中：M和β都是正常数.其中2β为sin函数的周期，影响滑移率切换控制的频率.

将式(13)代入式(12)得到：

(14)

与传统滑模控制类似，滑模极值搜索控制式(14)需要得到滑模可达条件．

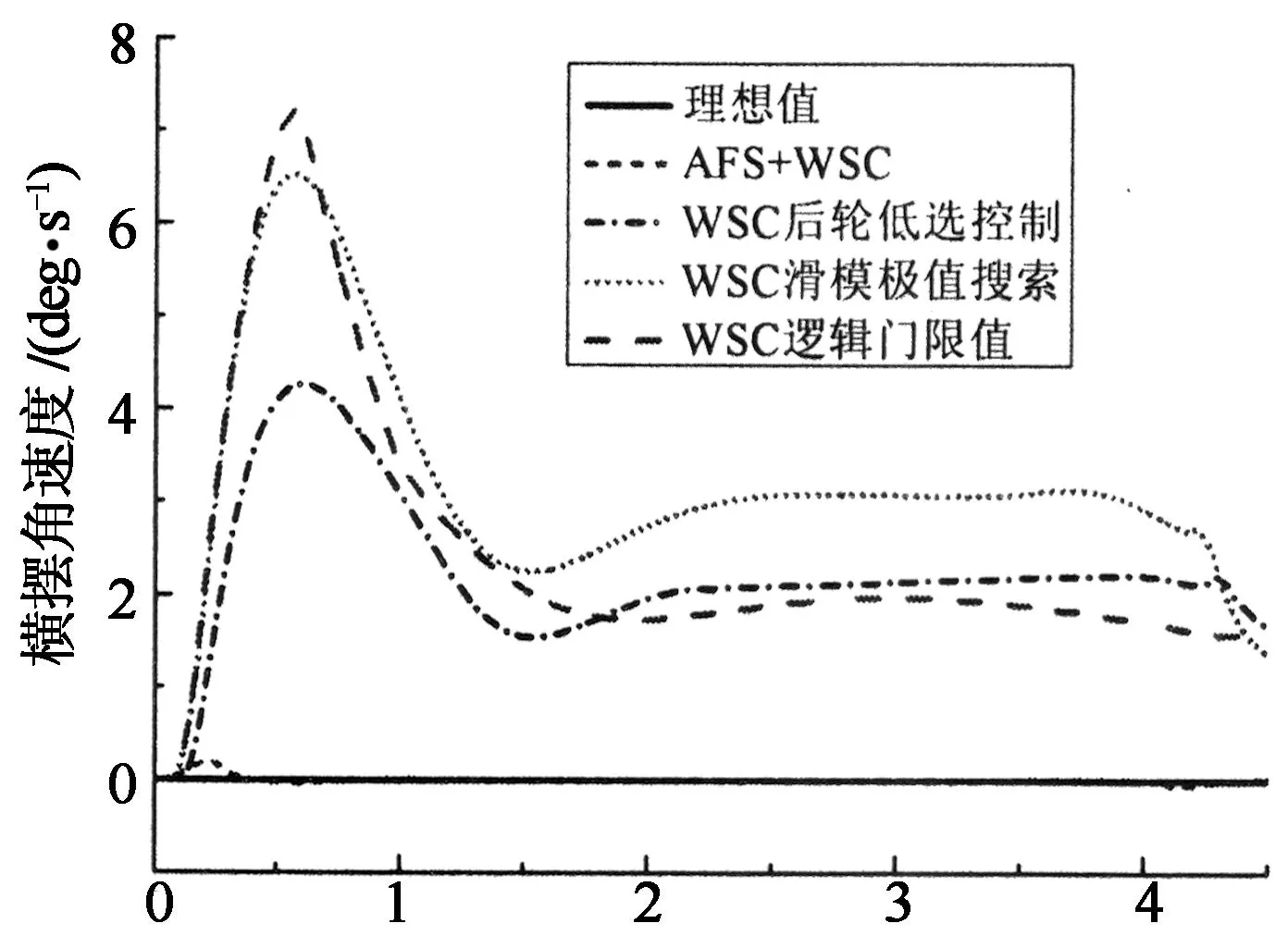
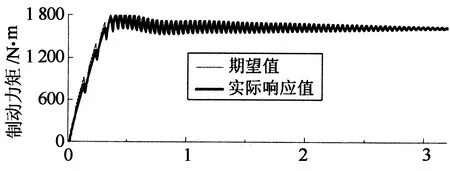
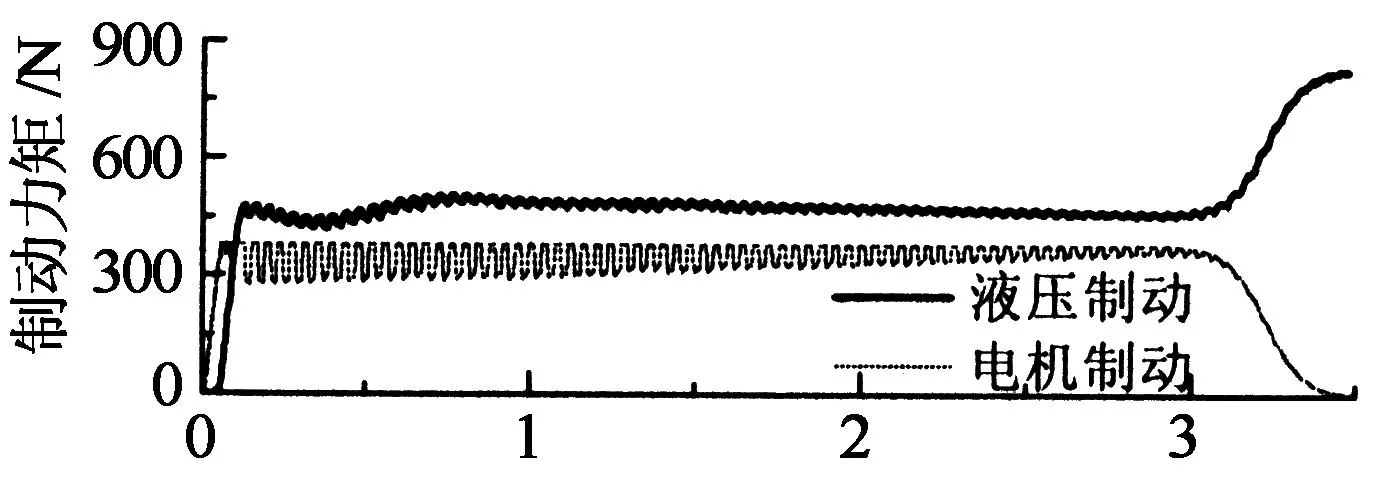
sin(πsi/β)是s(t)为自变量的周期函数，周期为2β.本文选择s(t)初始值在β与2β之间即β

sgn(s(t)-2β).

(15)

(16)

由sgn(γ(t))γ(t)=|γ(t)|可得不等式

(17)

根据李雅普诺夫滑模可到达条件：

(18)

得到

(19)

式(18)的等价形式为

(20)

由此可得 γ(t)→0即s(t)→β.

2) 令γ(t)=s(t)-2β ，同理可以证明:

(21)

由式(20)可推出s(t)→2β.

由1),2)证明，得到式(14)的滑模可到达条件如下：

(22)

以上分析表明s(t)在任意的初始值条件下，均会收敛于kβ，kβ即一系列滑模面，它保证了任意初始值条件下滑模可达性.

si=kβ=Fxi(ki,αi)+ρ t，

(23)

(24)

直线制动时αi=0，由上式可以看出，Fxi(Fxi数值为负)以-ρ的斜率不断减小，直到追踪到制动力的极值.∂Fxi(κi,αi)/∂κi代表制动力-滑移率曲线的斜率，当该斜率大于ρ/M时，制动力一直增加，接近制动力-滑移率曲线的极大值点，直到式(22)不能够满足时，停止搜索.

2.3AFS与WSC协调

转弯制动工况下，转向和制动两个系统之间存在着动力学上的相互影响、相互制约，而滑移率控制总是力求以当前路面条件下可能获取的最大制动力进行制动，由轮胎附着椭圆关系可知，这必然会引起侧向稳定性下降，造成AFS控制效果减弱.由本文提出的滑移率控制律可知，车辆转向时,

因此，式(22)右边的值增大，而极值搜索过程中，制动力-滑移率曲线的斜率∂Fxi(κi,αi)/∂κi越来越小，条件(22)保持时间缩短，造成Fxi增加的时间减少，因此制动力搜索点最后停下的位置偏离了极值点一定的距离，据轮胎附着椭圆关系可知，这为侧向力控制留下了一定的裕量，为增强AFS控制效果提供了可能.因此，本文引入驾驶员输入的前轮转角对滑移率控制律式(13)进行修正:

(25)

式中：ε是一个正常数.

将式(25)代入式(12)得出：

(26)

同式(14)，得出式(26)的滑模可达条件:

(27)

式中：ρ,M决定极值搜索的速度和最终的最大制动力工作的区域；ε决定制动力搜索点偏离极值点的距离.

对轮胎滑移率κi=-(vx-ωiR)/vx进行求导[8]，结合车轮动力学方程可得：

(28)

将式(25)代入式(28)得到各车轮总期望制动力矩为：

(29)

式中：假设车轮速度等于汽车车速；ωi为车轮转速；R为车轮半径；Tbi为各车轮总期望制动力矩；Iω为车轮转动惯量；Fxsum为总的轮胎制动力.其中，计算各车轮总期望制动力矩，需要轮胎纵向力信号，通过建立滑模观测器，对轮胎纵向力进行估计[9].

2.4制动力矩分配与执行

滑移率控制器得到的总期望制动力矩需要电机与电子液压复合制动实现，然而由于二者执行动力学差异[1]，传统静态控制分配在包含执行器动力学情况下易使实际响应力矩的复合效果与期望值之间有偏差，本文采用动态控制分配[10]实现电液力矩分配：

(30)

j∈{h,m}.

作为比较，本文采用链式递增法实现期望制动力矩的静态控制分配[11].图3为静态控制分配与动态控制分配力矩分配频域响应，可以看出动态控制分配高频阶段执行带宽更大的电机制动权重更大.

频率/Hz

频率/Hz

本文对电机与液压执行器建模，主要包括执行器实际可输出力矩和执行器动态响应特性，其中动态特性近似为一阶延时系统:[4]

(31)

式中：Tji为输出转矩；τj为时间常数．

对于执行器实际可输出力矩，一方面考虑液压制动和电制动位置约束和速率约束:

(32)

另一方面考虑最大再生制动转矩，其取决于车轮转速和电池荷电状态(SoC)，可由下式表达

Tmi,max(v,Iq,max,ωi)=p(v)(1-

(33)

式中：Iq,max∈[0,1]，为SoC指示系数，本文取值为0即假设电池有足够的充电空间；Tmi,n为电机峰值制动力矩；ωn为电机基速；p(v)为sigmoid函数，保证车速低于截止速度时，关闭电机再生制动功能.

p(v)=1/[1+e-kv(v-v0)]．

(34)

式中：kv为倾斜系数；v0为截止速度.

3数值仿真与验证

本文仿真工况设定为分离路面直线制动和分离路面转向制动等紧急制动工况，WSC均处于激活状态，验证所设计的控制策略(见表1)效果.

表1　控制策略对比

其中后轮低选控制表示后轮高附着一侧制动力选择与低附着一侧相同；滑模极值搜索与门限值控制均为四通道独立控制，逻辑门限控制取参考滑移率为0.2.直线制动时，协调控制与无协调控制策略一致，标示为“AFS+WSC”.车辆仿真参数见表2.

表2　车辆参数

3.1分离路面直线制动

工况设定：初始车速为25 m/s；路面摩擦因数，左侧0.8，右侧0.4.

图4为几种控制策略的横摆角速度变化曲线，可以看出AFS与WSC集成控制可以使横摆角速度接近理想值0，较好地补偿了由于左右制动力不均产生的干扰横摆力矩；其他3种单独WSC控制都无法跟踪理想值，但后轮低选控制因后轮制动力相同，产生的干扰横摆力矩变小，因此横摆角速度相对较小.图5为车辆制动轨迹曲线，AFS与WSC集成控制的最大侧向偏移为0.8 m，而3种单独WSC控制工况均出现较大的制动跑偏，其中逻辑门限值控制产生的侧向位移最大，为5.2 m；滑模极值搜索控制为5.1 m，但后者纵向距离为62.5 m，小于前者的69.6 m；后轮低选控制的侧向位移为4.08 m，小于滑模极值搜索的5.1 m，但其纵向制动距离为67.6 m，明显大于滑模极值搜索的62.5 m.其中，由于AFS调节，集成控制侧向偏移方向相反.

t/s

纵向距离/m

图6为轮胎滑移率变化曲线，可以看出0.25 s左右WSC搜索到了最优滑移率并保持稳定，说明本文所提出的滑模极值搜索算法可以自动搜索到最优滑移率.右侧低附路面最优滑移率偏小，符合路面附着系数越小最优滑移率也越小的趋势.图7所示为左前轮电液复合制动实际响应力矩跟踪期望值的效果曲线，可以看出动态控制分配能较好地跟踪期望值，而静态控制分配则无法跟踪期望值.图8所示为电机与液压制动力矩变化曲线，可以看出开始0～0.06 s内仅有电机制动，当其制动力矩达到饱和后，液压制动开始工作.仿真开始3 s后，随着车速降低，当电机转速低于电机基速时，再生制动力矩开始逐渐减小到0，与此同时液压制动逐渐增大以满足总期望制动力矩需求.可见制动过程中，除因最大扭矩380 N·m的约束条件限制，电机总是处于最大制动强度，最大化地进行了能量回收.

图6　轮胎滑移率变化曲线

t/s

t/s

3.2分离路面转弯制动

工况设定：初始车速为20 m/s；弯道内侧路面摩擦因数为0.4，外侧为0.8；1 s后开始向左转向，1 s内方向盘转角由0°转到84°.

图9显示，AFS与WSC协调控制可以较好地跟踪理想横摆角速度，无协调控制则在大横摆角速度时无法跟踪，3种WSC单独控制工况，均无法跟踪理想横摆角速度.

图10为转弯制动距离，可看出协调控制较无协调控制最大侧向位移增加了0.1 m，3种WSC单独控制时出现了较大的侧向滑移.图11显示，无协调控制时产生的质心侧偏角最大为0.22 rad，而协调控制仅为0.06 rad，单独WSC控制时因未实现理想转弯运动，产生的质心侧偏角均较小.图9～图11表明AFS与WSC协调控制较无协调控制可以显著提高车辆侧向稳定性，制动距离却未出现明显增大，而单独WSC控制均无法保证车辆转弯时的侧向稳定性.

t/s

t/s

t/s

t/s

t/s

纵向距离/m

t/s

图12为AFS与WSC协调控制产生的归一化轮胎纵向力，左侧轮胎快速稳定在0.4左右，而右侧稳定在0.8左右，说明WSC滑模极值搜索算法可以自适应路面附着系数的变化，快速搜索到轮胎的最大制动力.前轮转向时(1.0～2.0 s)，前轴左右轮归一化轮胎纵向力出现了明显的减小，这是由于AFS控制产生了车轮附加转角，造成轮胎纵向力减小的缘故.

t/s

4结论

针对分布式电驱动汽车，以实现车辆主动安全性同时兼顾制动能量回收为目标，考虑转向和制动两系统动力学上的相互影响和相互制约，提出一种AFS与电液复合制动的集成控制策略.通过对所提出控制策略进行仿真验证，主要得出以下结论：

1) 分离路面直线制动时，集成控制策略产生的横摆角速度接近0，侧向偏移为0.8 m，可以较好地回收制动能量，保证制动方向稳定性.滑移率控制器可自适应路面附着系数变化，不依赖参考滑移率即可快速搜索到最大制动力和最优滑移率.动态控制分配可使实际响应力矩更好地跟踪期望制动力矩.

2) 分离路面转弯制动时，WSC与AFS协调控制较无协调控制可以更好地跟踪理想横摆角速度，制动距离却未出现明显增大，且质心侧偏角明显相对较小，提高了车辆侧向稳定性.

参考文献

[1]CROLLA D A，CAO D. The impact of hybrid and electric powertrains on vehicle dynamics，control systems and energy regeneration[J]. Vehicle System Dynamics, 2012，50(S1)：95-109.

[2]KAWASHIMA K，UCHIDA T，HORI Y. Rolling stability control utilizing rollover index for in-wheel motor electric vehicle[J]. IEEJ Transactions on Industry Applications，2010，130(5)：655-662.

[3]余卓平，冯源，熊璐.分布式驱动电动汽车动力学控制发展现状综述[J].机械工程学报，2013，49(8)：105-114.

YU Zhuo-ping，FENG Yuan，XIONG Lu. Review on vehicle dynamics control of distributed drive electric vehicle[J]. Journal of Mechanical Engineering，2013，49(8)：105-114.(In Chinese)

[4]DE CASTRO R，ARAJO R E，TANELLI M，etal. Torque blending and wheel slip control in EVs with in-wheel motors[J]. Vehicle System Dynamics，2012，50(S1)：71-94.

[5]JING H H，LIU Z Y，LIU J S. Wheel slip control for hybrid braking system of electric vehicle[C]//Proceedings of 2011 International Conference on Transportation, Mechanical, and Electrical Engineering. New York: IEEE，2011:743-746.

[6]周兵，范璐，骆晨. 主动前轮转向变传动比曲线分析与设计[J]. 湖南大学学报:自然科学版，2014，41(2)：73-78.

ZHOU Bing，FAN Lu，LUO Chen. Analysis and design of the variable steering ratio curve of active front steering system[J]. Journal of Hunan University: Natural Sciences，2014，41(2)：73-78. (In Chinese)

[8]DINÇMEN E，GUVENÇ B A，ACARMAN T. Extremum seeking control of ABS braking in road vehicles with lateral force improvement[J].IEEE Transactions on Control Systems Technology，2012,22(1)：230-237.

[9]DRAKUNOV S，OZGUNER U，DIX P. ABS control using optimum search via sliding modes[J]. IEEE Transactions on Control Systems Technology, 1995，3(1)：79-85.

[10]HARKEGARD O. Dynamic control allocation using constrained quadratic programming[J]. Journal of Guidance, Control, and Dynamics，2004，27(6)：1028-1034.

[11]SATZGER C，DE CASTRO R，BÜNTE T. A model predictive control allocation approach to hybrid braking of electric vehicles intelligent vehicles[C]//Proceedings of IEEE Intelligent Vehicles Symposium(IV). New York: IEEE, 2014:286-292.

Integrated Control of Active Front Steering and Motor/Hydraulic Hybrid Braking in Distributed Electric Drive Vehicles

YUAN Xi-wen†, WEN Gui-lin, ZHOU Bing

(State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan Univ, Changsha, Hunan410082, China)

Abstract:A new control strategy was proposed by integrating active front steering and electro-hydraulic braking in distributed electric drive vehicles to ensure vehicle active safety by taking into account braking energy recuperation. The AFS controller was synthesized by means of sliding mode control. The wheel slip controller was designed with a hierarchical control structure. In the upper layer, sliding mode extremum-seeking algorithm was adopted to obtain the desired braking torque, and a dynamic control allocator considering different actuators bandwidths was employed to determine the optimal split between the electric and friction brake torque in the middle layer. In the lower layer, a hybrid actuator system consisting of the hydraulic brake and the electrical motor was designed on the basis of actuator position and rate constraints. The wheel slip control law was modified by introducing the road wheel angle factor considering the strongly coupled dynamics of steering and braking systems when braking-in-turn. Simulation results obtained with a 7-DoF vehicle model in MATLAB/Simulink environment have shown that the control strategy can significantly enhance vehicle directional stability and ensure braking energy recovery in split-μ straight-line braking, and can better track ideal yaw rate with vehicle lateral stability improvement when cornering.

Key words:vehicle engineering; motor/hydraulic hybrid braking; active front steering; energy recuperation; control strategy; extremum-seeking algorithm

中图分类号：U463.4

文献标识码：A

作者简介：袁希文(1985-)，男，山东沂水人，湖南大学博士研究生†通讯联系人，E-mail:lntsh854@hnu.edu.cn

基金项目：国家自然科学基金资助项目(51275162), National Natural Science Foundation of China(51275162); 吉林大学汽车仿真与控制国家重点实验室开放基金资助项目(20121109);高等学校博士学科点专项科研基金资助项目(20120161130001);湖南大学汽车车身先进设计制造国家重点实验室自主课题(71275003)

*收稿日期：2014-12-20

文章编号：1674-2974(2016)02-0028-08