卫星复合材料桁架结构多级优化设计方法
2016-04-25苏若斌陶炯鸣孔祥森
苏若斌 陶炯鸣 孔祥森
(上海卫星工程研究所,上海 200240)
卫星复合材料桁架结构多级优化设计方法
苏若斌 陶炯鸣 孔祥森
(上海卫星工程研究所,上海 200240)
针对卫星用复合材料桁架结构,提出一种多级优化设计方法,对复合材料桁架结构的空间构型、几何参数以及材料铺层角度开展协同优化设计。该方法能够在缩减优化问题求解规模,提高解算精度的同时,获得兼顾结构刚度、强度、稳定性、质量以及在轨热变形的综合最优结果。最终通过工程算例,验证了文中提出优化设计方法的有效性。
卫星;复合材料;桁架结构;多级优化设计
1 引言
复合材料桁架结构有着空间构型适应能力强、承载大、质量轻的优点,广泛应用于卫星承力结构、星上重要仪器设备的安装结构以及特殊连接结构[1]。考虑到复合材料的可设计性,将桁架结构的几何参数与材料参数协同设计,充分发挥复合材料的潜力,对于进一步降低结构质量,提升桁架结构综合性能具有重要意义。
近年来,国内外学者针对复合材料结构的优化设计开展了广泛的研究,优化内容主要集中在复合材料结构的构型布局、刚度、强度、稳定性、结构质量、气动性能等多方面,部分研究以单目标最优为设计目的,部分研究以达到多目标协同最优为目的。其中,比较典型的如张铁亮等[2]针对复合材料加筋板结构的构型布局进行了优化设计工作;Schmit等[3]以强度、刚度为约束条件,以复合材料的铺层厚度和铺层角度为设计变量,进行了多目标协同优化设计工作;Haftka等[4]以结构稳定性最优为目标,建立了以复合材料铺层厚度和铺层角度为设计变量的优化设计模型;Ji-Ho Kang等[5]利用遗传算法,研究了轴压复合材料板和加筋板质量最小时的材料铺层参数;王琦等[6]针对复合材料前掠翼结构,提出了一种综合考虑气动、强度、刚度、稳定性的优化方法。
上述研究大多应用于解决飞机复合材料结构设计中的实际问题,但是考虑到卫星复合材料桁架结构的应用特点,优化设计时在满足结构刚度、强度、稳定性、结构质量等要求的同时,还要求结构在轨具有较高的尺寸稳定性,避免桁架在轨工作时由于受光照不均匀产生剧烈的热变形,影响有效载荷在轨指向精度。
结合以上需求,本文基于OptiStruck结构优化软件,提出一种卫星复合材料桁架结构的多级优化设计方法,结合卫星桁架结构的实际需求,在减小优化问题的求解规模的同时,实现桁架结构的刚度、强度、稳定性、质量、在轨热变形等综合最优。
2 多级优化方法
本文提出的多级优化设计方法的流程如图1所示,整个优化设计过程分为三个层级:第一层级优化设计结合桁架结构的包络空间、安装约束、质量限制等要求,以刚度最优为目标进行拓扑结构优化设计;第二层级在第一层级优化结果的基础上,在满足结构强度、刚度、稳定性的前提下,以质量最小为目标进行尺寸优化设计;第三层级在前两级优化结果的基础上,以结构在轨热变形最小为设计目标进行复合材料的铺层优化设计。为了避免出现优化结果退化的情况,在次级优化模型中增加综合协调约束,约束次级优化结果的刚度、强度、稳定性等不低于上级模型的计算结果,最终实现结构设计的综合最优。
该优化设计方法,每一层级均为单目标优化问题,求解规模小,并且将结构的刚度、稳定性等宏观属性,与桁架局部强度裕度、材料铺层厚度、角度等微观属性分别进行优化,便于在单元尺度上进行协调,对宏观特性的优化设计采用单元较稀疏的计算模型,对微观特性的优化设计采用单元较细密的计算模型,能够利用有限的计算资源,获得更高精度的优化结果。

图1 多级综合优化流程Fig.1 Typical process of the multilevel optimization method
2.1 拓扑优化
拓扑优化采用正交惩罚材料密度法(Solid Isotropic Material with Penalization Model,SIMP),优化时将拓扑模型的每个“单元密度”作为设计变量,该密度在0~1之间连续取值,1表示该单元位置处的材料很重要需要保留,0表示该单元处的材料可以去除[7]。考虑到卫星桁架结构的实际特点,结合文献[8]的研究,建立以桁架刚度最优为目标的拓扑优化数学模型如下:

式中:ρ为结构单元的相对密度;n为单元数目;(ρ)为平均频率;ωj为第j阶特征频率;ω0、s为给定的参数,用于调整目标函数;ω*j为第j阶频率的权值系数;f为需要优化的低阶频率的阶次;M为优化模型的总质量矩阵;K为优化模型的总刚度矩阵;φj为第j阶振型的向量;m为优化后的桁架结构总质量;m0为初始拓扑优化结构总质量;mi为优化后的单元质量;ρmin设计变量的下限,目的是防止单元刚度矩阵奇异(一般取值ρmin≈0);αU为质量分数上限,其具体数值可以通过式(2)计算得到。

式中:mdesign为桁架容许的最大质量,数值由卫星方案论证分配确定。
优化分析计算时,须要将桁架结构与卫星平台和有效载荷(或单机)的安装界面定义为不可约束区域,保证优化结束后保留相应位置的材料。并且考虑到复合材料桁架设计初期,尚未进行详细的铺层设计,材料参数以层合板等效力学参数的形式给出,根据卫星复合材料桁架结构的设计经验,接头铺层采用准各向同性铺层,参考铺层顺序为[+45°/0°/-45°/90°],杆件铺层采用30°方向铺层,参考铺层顺序为[+30°/-30°/03°/-30°/+30°]。
2.2 尺寸优化
拓扑优化主要目的是利用有限的结构质量,获得刚度最优的桁架空间构型,而对于桁架结构的稳定性、强度等因素,受限于单元尺度的制约,考虑较少。因此在一级优化模型的基础上,建立二级优化模型,以结构质量最小为优化目标,建立综合考虑结构强度、刚度、稳定性的数学模型如下:
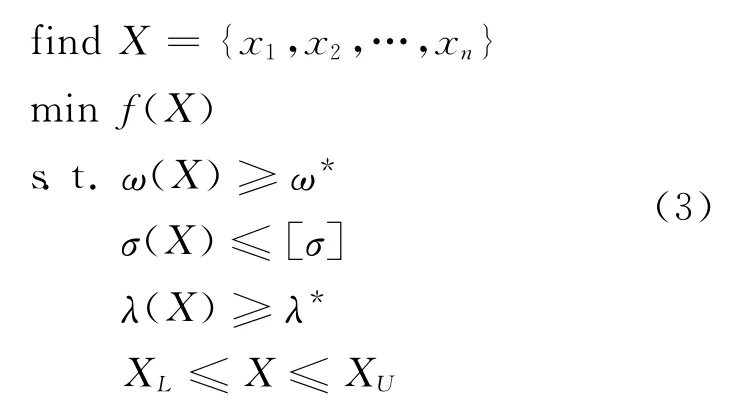
式中:f(X)为优化目标,针对卫星复合材料桁架结构,一般取桁架质量;X为所有的设计变量集合;[σ]为复合材料的许用应力;λ*为桁架的最小屈曲因子,取值一般不低于2[1];XL和XU分别为X的下限值和上限值。
需要注意的是,式(3)中的参数ω*是为避免出现刚度退化而设置的刚度协调条件,取值应保证不低于上述拓扑优化获得的结构刚度值;X主要为杆件截面尺寸参数的集合,如为圆形杆件,即为每根杆件的外圆及内壁直径,如为矩形杆件,即为每根杆件矩形截面的边长以及壁厚。
2.3 铺层优化
通过复合材料桁架结构的热膨胀系数设计,可以将桁架结构的热变形控制在允许的范围内,一般可以通过合理的铺层设计(铺层厚度及铺层角度),实现复合材料结构在某些方向上的“零热膨胀”效果。因此考虑在一、二级优化结果的基础上,建立三级优化模型,以复合材料桁架结构空间热变形最小为目标,进行铺层优化设计。
考虑到卫星复合材料桁架结构的接头主要为单向板铺层模压成形,杆件主要为缠绕成形,其中单向板的厚度以及缠绕丝的直径具有标准系列,即铺层厚度一般具有固定数值系列,因此铺层优化设计变量主要为铺层角度,建立复合材料铺层优化的数学模型如下:

式中:Dtemp为给定温度场下,结构在轨最大绝对热变形;θ为铺层角度;θL以及θU为铺层角度的上下限值。
须要注意的是,式(4)中的ω*和λ*是为避免优化结果退化而增加的协调约束,取值不低于上层模型的优化结果。铺层优化结束后,为避免材料分层,应保证同一角度的铺层连续出现的次数小于4。
3 算例
本文以某卫星大型可展开天线的安装桁架为例,利用上述多级优化方法进行优化设计。
桁架结构主要作为大型天线及天线馈源阵基板的安装基础,桁架底部与卫星平台顶板连接,桁架在轨工作状态以及发射状态的安装包络(优化设计区域)如图2所示。

图2 桁架设计包络区域Fig.2 Spatial restriction of the composite material truss
3.1 拓扑优化
根据图2设计包络建立拓扑优化设计模型如图3所示,优化时底部固支,设定桁架底部以及桁架与天线、馈源阵基板的安装区域为不可优化区域。桁架材料选取M55J碳纤维复合材料,按照30°方向铺层,初始拓扑优化结构总质量为6.7t,桁架结构的质量要求小于105kg,由式(2)可知,质量分数上限取0.015 7。

图3 拓扑优化设计模型Fig.3 Topology optimization model
拓扑结果及对应的二级优化模型如图4所示。其中二级优化模型是根据拓扑结果获得的桁架结构空间构型分布,结合卫星桁架结构设计经验确定的,其杆件采用截面尺寸为Φ50mm、壁厚3mm的圆管,建立二级优化模型获得桁架质量为101.8kg。

图4 优化结果及二级优化模型Fig.4 Result of topology optimization and the secondary optimization model
将二级优化模型放入整星模型中,进行初始仿真分析,分析结果见表1。其中最大应力是指在运载火箭提供的准静态过载工况下获得的应力最大值,热变形是在热控提供的在轨极端温度工况下获得的桁架结构的最大绝对热变形。由表1的数据可以看出,二级模型的分析结果满足各项指标要求。在常规卫星复合材料桁架设计中,该设计即可作为最终定型设计。
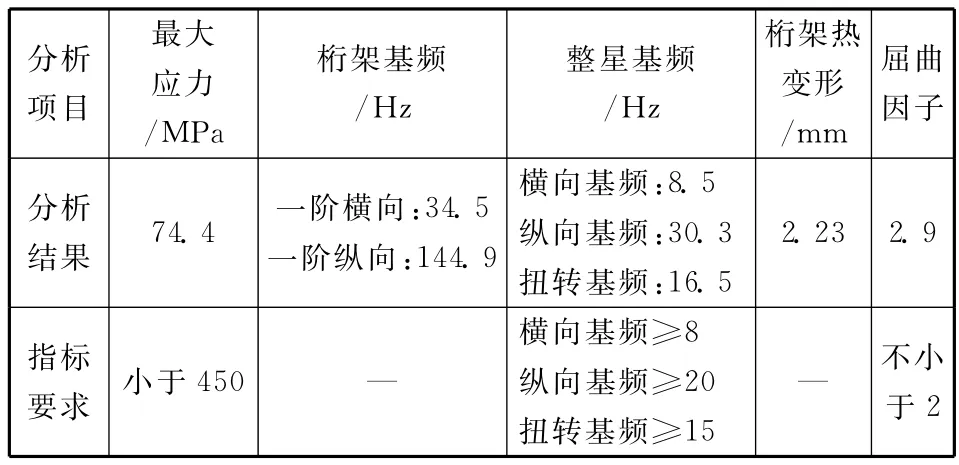
表1 初始仿真分析结果Table 1 Result of initial simulation
3.2 尺寸优化
根据上述拓扑优化结果建立的二级优化模型,进行进一步的优化设计。将杆件截面尺寸作为优化设计变量,优化设计目标为质量最小,优化约束条件为满足基频不小于35Hz,屈曲因子不小于2.9,最大应力小于450MPa。考虑到桁架内部各杆件的受力情况各不相同,将桁架的优化区域分为顶部、中部和底部三部分,分别进行尺寸优化。优化模型以及设计变量如图5所示。

图5 尺寸优化模型分区及设计变量Fig.5 Size optimization model and design variables
设计变量与目标函数的关系如图6所示,可以看到,随着杆件截面尺寸的不断调整,目标函数呈现减小的趋势,随着迭代次数的增加,目标函数最终稳定到76.1kg,此时优化计算达到收敛。由设计变量的最终收敛数值可以看出,优化结果呈现底部杆件较为“粗壮”,顶部杆件较为“纤细”的结果,这与桁架结构底部受载更为严苛的情况相吻合。

图6 目标函数与截面参数的关系Fig.6 Relationship between section parameters and objective function
最终获得的设计变量数值须要进行工艺圆整后,方可进行生产加工,并且由于杆件壁厚的改变,须要将杆件的材料铺层进行适应性调整,最终优化结果见表2。
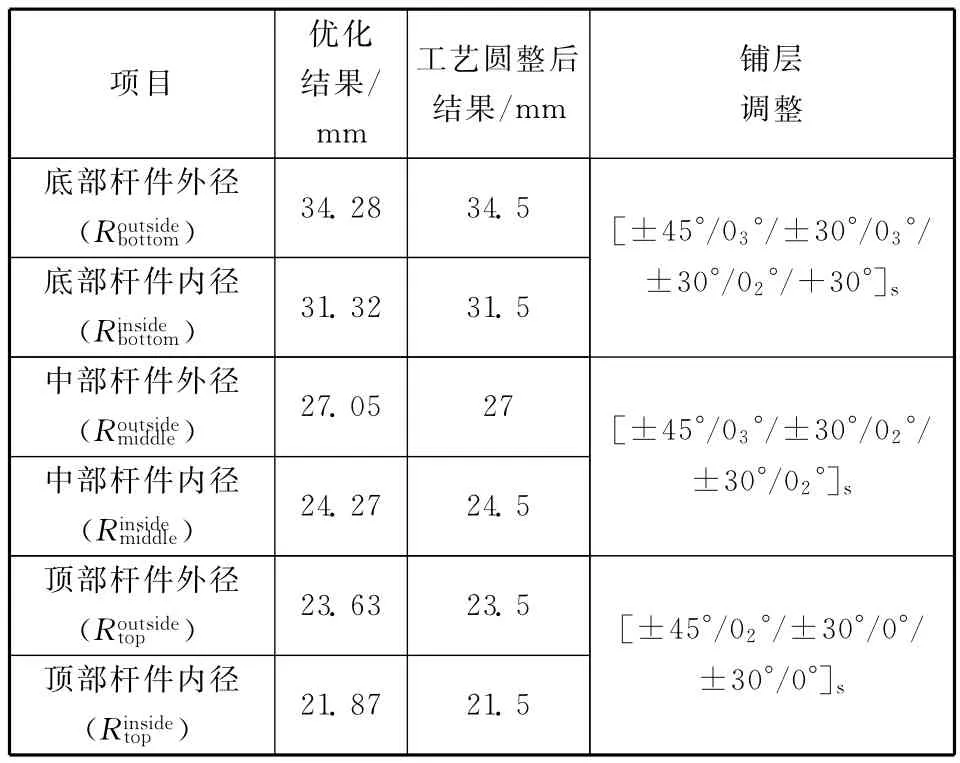
表2 设计变量圆整及材料铺层变化情况Table 2 Adjustment of design variables and layout angle
3.3 材料铺层优化
根据第一、二级优化结果建立三级优化模型,进行桁架材料铺层优化设计,考虑到桁架接头的受力情况较为复杂,不具有明显的方向性,因此采用综合性能较好的准各向同性铺层。设计变量为杆件的铺层角度,取值范围为-90°~90°,优化目标为桁架结构的在轨绝对最大热变形数值最小。为避免出现优化结果退化的情况,增加综合协调约束条件,使得桁架基频不小于35Hz,屈曲因子不小于2.9,最大应力小于450MPa。考虑到桁架结构的材料铺层数目较多,如将每一铺层的角度均作为设计变量,则优化问题计算量会急剧增大,最终可能较难获得可用的收敛结果。优化设计时,将设计变量根据顶部、中部和底部杆件分为三部分,每部分相同的铺层角度作为一个设计变量,获得的目标函数与设计变量的关系如图7所示。

图7 目标函数与铺层角度的关系Fig.7 Relationship between layout angle and objective function
可以看出,复合材料不同的铺层方式对桁架结构的热变形情况影响较为明显,随着铺层角度的调整,桁架结构热变形急剧减小,随着迭代次数的增加,最终热变形趋于稳定。对比优化前后,结构最大热变形由2.23mm减小为0.85mm,降低了61.8%。通过尺寸圆整,最终获得底部杆件的铺层形式为[±50°/03°/±18°/03°/±18°/02°/+18°]s,中部杆件的铺层形式为[±60°/03°/±15°/02°/±15°/02°]s,顶部杆件的铺层形式为[±48°/02°/±20°/0°/±20°/0°]s。
3.4 优化校核
三级优化完成后,根据最终结果建立桁架分析模型,进行仿真分析,结果如表3所示,最终满足卫星各项指标要求,且在结构刚度、强度、质量以及在轨热变形等多方面获得明显改善。
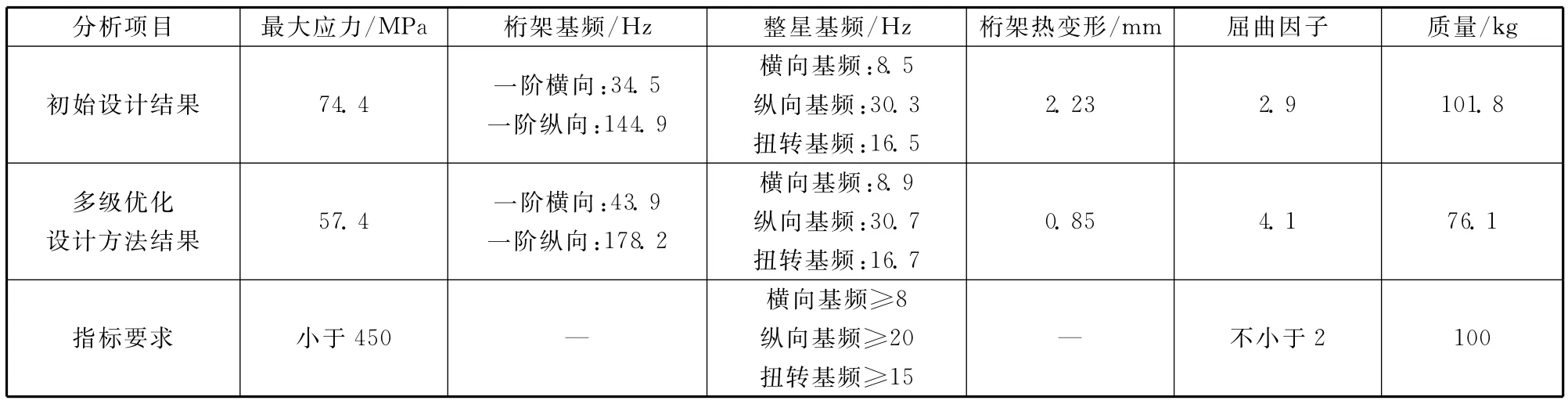
表3 根据优化设计结果的仿真分析Table 3 Simulation analysis based on the optimal result
4 结束语
本文对卫星复合材料桁架结构提出了一种多级优化设计方法,将整个复合材料桁架结构优化设计问题分为3个层级,较好地解决了结构设计中的多变量耦合问题,避免了同时对大量设计变量进行优化计算,有效降低了结构优化分析的非线性程度。通过算例验证表明,本文的优化设计方法合理可行,效果明显,可以应用于卫星复合材料桁架结构的优化设计。
(References)
[1]陈烈民.航天器结构与机构[M].北京:中国科学技术出版社,2005 Chen Liemin.Spacecraft structure and mechanism[M].Beijing:China Science and Technology Press,2005(in Chinese)
[2]张铁亮,丁运亮.复合材料加筋壁板的结构布局优化设计[J].南京航空航天大学学报,2010,42(1):8-12 Zhang Tieliang,Ding Yunliang.Structural layout optimization of composite stiffened panel[J].Journal of Nanjing University of Aeronautics &Astronautics,2010,42(1):8-12(in Chinese)
[3]Schmit Jr LA,Farshi B.Optimum laminated design for strength and stiffness[J].International Journal of Numerical Method in Engineering,1997,7:519-536
[4]Haftka RT,Walsh RL.Stacking-sequence optimization for buckling of laminated plates by integer programming[J].AIAA,1992,30(3):814-819
[5]Ji Ho Kang.Minimum weight design of compressively loaded composite plates and stiffened panels for post buckling strength by genetic algorithm[J].Composite Structure,2005,69:239-246
[6]王琦,金海波,丁运亮.复合材料飞机结构综合优化设计技术研究[J].机械科学与技术,2010,26(11):1381-1384 Wang Qi,Jin Haibo,Ding Yunliang.On optimal design of composite aircraft structure[J].Mechanical Science and Technology for Aerospace Engineering,2010,26(11):1381-1384(in Chinese)
[7]洪清泉,赵康,张攀,等.OptiStruct &HyperStudy理论基础与工程应用[M].北京:机械工程出版社,2012 Zhao Qingquan,Zhao Kang,Zhang Pan,et al.The theoretical basis and engineering application of OptiStruct&HyperStudy[M].Beijing:China Machine Press,2012(in Chinese)
[8]Ma Z D,Kikuchi N.Topological design for vibrating structures[J].Computer Methods in Applied Mechanics and Engineering,1995,121:259-280
(编辑:李多)
Multilevel Optimization Method of Composite Truss Structure for Satellite
SU Ruobin TAO Jiongming KONG Xiangsen
(Shanghai Institute of Satellite Engineering,Shanghai 200240,China)
In this study,a multi-level method is proposed for the optimal design of composite truss structures for satellites.This novel optimization method conducts collaborative optimization design by taking the composite truss structures’spatial configuration,geometrical parameters and lay-up angle into consideration simultaneously.The optimization method is able to decrease the computational scale and improve the calculation precision.Meanwhile,the overall optimal results referring to stiffness,strength,stabilization,mass and in-orbit deformation of composite truss structure can be obtained.Finally the feasibility of the optimization method is verified by applying it to an engineering example.
satellite;composite material;truss structure;multilevel optimization
V43.42
:ADOI:10.3969/j.issn.1673-8748.2016.01.006
2015-12-24;
:2016-01-11
苏若斌,男,工程师,研究方向为卫星结构设计。Email:suruobin@126.com。
