一种重力测量卫星静电加速度计在轨标定算法

辛宁邱乐德张立华刘乃金

（1中国空间技术研究院通信卫星事业部，北京 100094）（2航天东方红卫星有限公司，北京 100094）

一种重力测量卫星静电加速度计在轨标定算法

辛宁1邱乐德1张立华2刘乃金1

（1中国空间技术研究院通信卫星事业部，北京 100094）（2航天东方红卫星有限公司，北京 100094）

静电加速度计是低低跟踪（SST－LL）重力测量卫星的关键载荷之一，其性能直接影响地球重力场空间变化率的测定结果。为了确保静电加速度计长期在轨工作，结合扩展卡尔曼滤波估计算法，提出了一种应用动力学方法确定静电加速度计校准参数的算法。首先建立静电加速度计及K频段测距（KBR）系统的量测模型；然后将高精度地球重力场模型和静电加速度计观测数据代入扩展卡尔曼滤波算法的状态方程中，将KBR系统观测数据代入观测方程中，建立静电加速度计在轨标定模型。数学仿真结果表明：静电加速度计的标度因子和零偏估计误差均在0.2%以内，实现了卫星静电加速度计较为精确的标定。

重力测量卫星；静电加速度计；K频段测距系统；在轨标定

1 引言

静电加速度计是低低跟踪（SST－LL）重力测量卫星的关键载荷，用于精确测量作用于卫星上的非保守力加速度，其测量精度达到3×10－10m／s2。卫星在轨运行过程中，由于受空间环境辐射、各元件性能退化的影响，加速度计的零偏误差、标度因子具有不确定性［1］，直接影响重力场反演的精度。因此，为了反演高精度和高分辨率的地球重力场模型，提高重力测量卫星的精密定轨精度，进行加速度计的在轨标定研究具有重要的意义。

文献［2］中利用旋转卫星法开展了加速度计的在轨标定研究，对于评估加速度计在轨性能具有一定的指导意义，但是其中需要卫星的姿态机动、质心调节等一系列复杂的操作，而且标度因子检验和坐标轴偏差测量无法满足预期精度。文献［3］中利用加速度计在轨测量非保守力数据，并与标准的非保守力模型进行比对给出标定结果，但是非保守力模型（如大气模型）往往很难准确描述卫星所受的非保守力，因此标定结果精度较差。文献［4］中将GPS精密定轨数据与根据重力场模型和加速度计实时测量数据计算出的轨道对比，利用Batch估计方法给出加速度计的校准参数。该方法建立了GPS与加速度计之间的数据联系，对于重力测量卫星的总体设计具有一定的指导意义。但由于GPS精密定轨数据中并未包含卫星的加速度信息，因此Batch估计方法中的系统状态转移矩阵非常复杂，同时采用积分的方法对轨道进行估计会使观测噪声累积，且一般采用一天的数据估算一次校准参数，使Batch估计方法的估计值可能无法收敛。文献［5］中利用重力场反演方法（能量法）确定加速度计校准参数，基本原理是利用现有的重力场模型计算卫星高度处的扰动位，与利用加速度计观测值计算的扰动位进行比较，通过最小二乘法确定校准参数，但该方法依赖于先验重力场模型与数据处理方法，根据不同的重力场模型计算出的加速度计标度因子和零偏误差并不相同。总体说来，以上静电加速度计的标定方法均仅基于高低跟踪（高轨GPS卫星跟踪低轨卫星）的重力场测量模式，因此无法有效消除由非保守力模型、GPS定轨误差、重力场模型等引起的系统误差，加速度计标定精度有待提高。

本文从重力测量卫星工程设计出发，在文献［4］的基础上，利用低低跟踪（低轨卫星跟踪低轨卫星）的重力场测量模式，将重力测量卫星另一个关键载荷K频段测距（KBR）系统观测到的星间加速度［6］代替双星差分GPS数据作为系统观测量，并利用高精度的地球重力场模型，基于动力学方法建立静电加速度计的量测模型，并利用扩展卡尔曼滤波算法实现静电加速度计参数的在轨标定。由于星间加速度可由KBR系统直接输出，因此本文算法无须进行积分，可大大简化估计算法中的系统状态转移矩阵，建模简便，同时采用低低跟踪的重力场测量模式进行数据差分可有效消除GPS定轨误差、先验重力场模型引起的系统误差。此算法的可行性通过数学仿真进行了验证，可为重力测量卫星工程应用提供参考。

2 静电加速度计在轨标定算法

静电加速度计参数标定算法的基本原理为：根据静电加速度计和KBR系统的量测模型构建静电加速度计在轨标定的观测方程，再结合高精度重力场模型，利用扩展卡尔曼滤波算法分离出具有线性特征的静电加速度计误差分量，由此来确定静电加速度计的零偏误差和标度因子，从而实现静电加速度计的在轨标定。

2.1 静电加速度计量测模型

静电加速度计在动态设计良好并进入稳态后，输出值可表示为［7］

式中：静电加速度计的标度因子s＝diag（s1，s2，s3），s1，s2，s3为静电加速度计标度因子在3轴方向的分量；为在卫星本体坐标系下的非引力加速度，卫星本体坐标系的原点为卫星质心，x轴垂直于卫星轨道平面，y轴为卫星飞行方向，z轴为卫星对地指向；b为零偏误差；An为观测高斯白噪声。

由式（1）可得

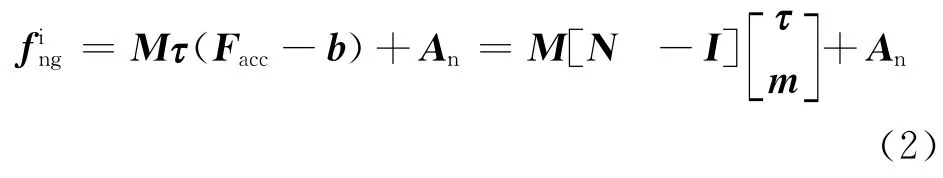
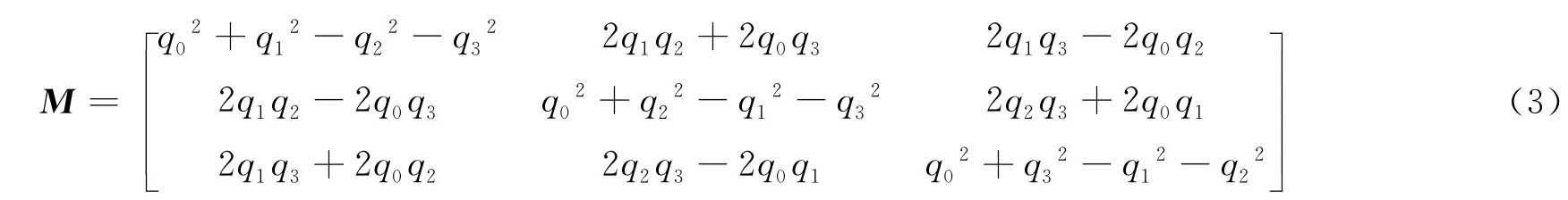
式中：q＝［q0q1q2q3］T，为星敏感器观测的姿态四元数。

根据地球重力场模型可确定卫星所受的引力加速度fg［5］，则卫星加速度可表示为

2.2 KBR系统量测模型

KBR系统观测值包括星间距离、星间速度及星间加速度。设卫星A和卫星B在地心惯性坐标系中的质心位置分别为rA和rB，则星间距离rAB的大小为式中：和为卫星A和卫星B的加速度；和为GPS数据精密定轨后得到的卫星A和卫星B的速度。

以上观测值均可通过文献［6］中构建的KBR仿真系统中的卫星轨道姿态模块获取。

2.3 静电加速度计参数的扩展卡尔曼滤波估计

静电加速度计参数标定模型的系统状态变量为X＝［τAmAτBmB］T，则其系统状态方程为

式中：τA，τB和mA，mB是计算得到的卫星A和卫星B的τ和m。

将式（2）和式（4）代入式（9），得系统观测方程为

式中：H（t）为状态转移矩阵，如式（12）所示，t为积分时间；和分别为卫星A和卫星B根据地球重力场模型计算的引力加速度；Zn为测量误差。

式中：MA和MB分别为卫星A和卫星B本体坐标系到地心惯性坐标系的转换矩阵；NA和NB分别为卫星A和卫星B的静电加速度计输出。

给定初始状态估计值＾X（t0）及初始估计均方差误差P（t0），利用扩展卡尔曼滤波算法即可估计出两颗卫星静电加速度计的标度因子和零偏误差，其迭代过程如式（13）～（17）所示。

3 数学仿真

静电加速度计在轨标定算法的仿真流程见图1。

图1 静电加速度计在轨标定算法仿真过程Fig.1 Simulation procedure of electrostatic accelerometer on－orbit calibration algorithm

在卫星轨道和姿态模拟器中［8］，地球引力场模型采用120阶EMG96模型；大气阻力模型采用大气阻力温度模型（Drag Temperature Model，DTM），大气阻力系数为2.2；在太阳光压摄动模型中，太阳光压反照系数为0.5；地球磁场模型采用13阶IGRF2005模型。根据卫星轨道和姿态模拟器输出的卫星位置、速度和姿态四元数，模拟生成KBR系统观测值、静电加速度计观测值、GPS观测值及星敏感器观测值，将这些观测值代入到扩展卡尔曼滤波算法中，得到静电加速度计的在轨标定结果。

卫星的飞行姿态为三轴对地定向模式，卫星A和卫星B初始轨道参数见表1。

表1 两颗卫星的初始轨道参数Table 1 Initial orbit parameters of two satellites

KBR系统仿真值如图2所示，由于轨道周期为5600s，并且轨道偏心率不为零，因此星间距离序列表现为周期为5600s、振幅为2km的余弦波形。星间加速度值如图3所示，其表现为周期为5600s、振幅为0.002 5m／s2的余弦波形。根据非保守力模型，卫星A和卫星B的静电加速度计的仿真值如图4和图5所示，由于在飞行过程中为卫星B领飞，卫星A跟飞，因此卫星B在y轴的非保守力加速度要略大于卫星A，其余两个方向则基本保持一致。

图2 KBR系统测距观测值Fig.2 KBR system range observation

图3 卫星A与卫星B星间加速度观测值Fig.3 Range acceleration observation between satellite A and B

图4 卫星A加速度计输出值Fig.4 Accelerometer observation of satellite A

图5 卫星B加速度计输出值Fig.5 Accelerometer observation of satellite B

静电加速度计标定算法仿真中，地球引力场模型采用120阶TJGRACE02S模型［9］和120阶EGM96模型［10］。卫星A静电加速度计的三轴标度因子为1.0，零偏误差为5×10－5m／s2；卫星B静电加速度计的三轴标度因子为1.0，零偏误差为5×10－5m／s2；星敏感器的姿态确定精度为0.05mrad；KBR系统的偏置误差为1μm，系统噪声误差为0.5μm。GPS接收机的定轨精度为1cm，测速精度为0.1mm／s；卫星质量为500kg；转动惯量为diag（80，420，470）kg·m2；仿真中以1d的轨道弧长为单位，对10d的轨道弧长进行10次标定，仿真结果中给出了x轴方向的标定结果（y轴方向和z轴方向与x轴方向具有相同的结论），如图6～9所示。标度因子和零偏误差平均统计结果如表2所示。

由图6～9可以看出：在不同时间，静电加速度计的标度因子和零偏误差的标定值是波动的，这说明标度因子和零偏误差并不是固定不变的。因此，对静电加速度计数据精度要求较高的用户，建议每天或半天甚至数小时估计一次标度因子和零偏误差，并根据其时间变化规律进行曲线拟合。同时，可以看出：参考地球重力场模型的精度对校准参数仍会有一定的影响，但总体来说，计算结果相差不是很大，因而可认为此算法校准加速度数据对先验地球重力场模型的选择并不是很敏感。

图6 卫星A静电加速度计x轴方向标度因子标定结果Fig.6 Calibration results of scale factor along x axis of satellite A electrostatic accelerometer

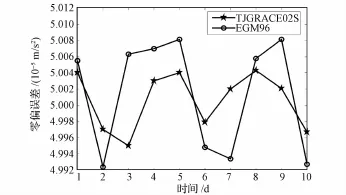
图7 卫星A静电加速度计x轴方向零偏误差标定结果Fig.7 Calibration results of bias along xaxis of satellite A electrostatic accelerometer

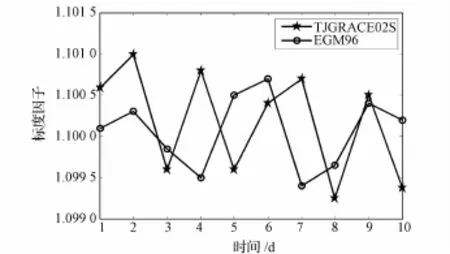
图8 卫星B静电加速度计x轴方向标度因子标定结果Fig.8 Calibration results of scale factor along x axis of satellite B electrostatic accelerometer

图9 卫星B静电加速度计x轴方向零偏误差标定结果Fig.9 Calibration results of bias along xaxis of satellite B electrostatic accelerometer

表2 双星静电加速度计标度因子和零偏误差均方差统计结果Table 2 Scale factor and bias calibration error of satellite A and B

由表2可以看出，利用EGM96和TJGRACE02S模型计算出的标度因子和零偏误差，估计误差均在0.2%以内，从统计角度而言，并无显著差别，而从标度因子和偏差参数的变化规律来看，也十分相似（个别地方有差别），这说明本文给出的算法稳定性好，也说明EGM96模型与TJGRACE02S模型有较好的一致性。

4 结论

（1）本文提出的在轨标定算法，充分考虑到静电加速度计和KBR系统观测数据之间的数据联系，建立了静电加速度计参数标定的状态方程和观测方程，并采用扩展卡尔曼滤波对双星的加速度计进行实时在轨补偿。

（2）本文算法重点解决了动力学方法中由于要进行轨道积分而导致状态转移矩阵十分复杂的问题，有效简化了在轨标定算法结构，且计算量有所减少。

（3）利用不同的参考地球重力场模型分别进行数学仿真验证，数值分析结果说明该方法是有效的。此外，该方法对先验地球重力场模型的选择不太敏感，但与所选参考地球重力场模型的精度仍有一定关系，因而在静电加速度计标定时应尽量选择精度较高的模型。

（4）本文算法也适用于单独对尺度因数或零偏误差进行在轨标定的情况。为了进一步提高估计精度，可以充分利用该算法对尺度因数和零偏误差的标定结果，以及更多的可以估计到的误差结果对系统进行优化，使系统达到最优。

（References）

［1］周泽兵，白彦峥，祝竺，等.卫星重力测量中加速度计在轨参数校准方法研究［J］.中国空间科学技术，2009，29（6）：74－80 Zhou Zebing，Bai Yanzheng，Zhu Zhu，et al.In－orbit calibration methods of accelerometer parameters on satellite－borne gravimetry［J］.Chinese Space Science and Technology，2009，29（6）：74－80（in Chinese）

［2］祝竺，张晓敏，周泽兵.利用旋转卫星法开展加速度计在轨检验研究［J］.宇航学报，2010，31（5）：1362－1367 Zhu Zhu，Zhang Xiaomin，Zhou Zebing.In－orbit verification for accelerometers using rotating spacecraft method［J］.Journal of Astronautics，2010，31（5）：1362－1367（in Chinese）

［3］Visser Pnam，Ijssel J.Verification of CHAMP accelerometer observations［J］.Advance in Space Research，2003，31（6）：1905－1910

［4］Tom V，Eelco D，Pieter V.CHAMP and GRACE accelerometer calibration by GPS－based orbit determination［J］.Advance in Space Research，2009，24（8）：45－50

［5］徐新禹，李建成，王正涛，等.利用参考重力场模型基于能量法确定GRACE加速度计校准参数［J］.武汉大学学报（信息科学版），2008，33（1）：72－75 Xu Xinyu，Li Jiancheng，Wang Zhengtao，et al.Calibration of GRACE accelerometer using reference gravity field model based on energy balance approach［J］.Geomatics and Information Science of Wuhan University，2008，33（1）：72－75（in Chinese）

［6］辛宁，邱乐德，张立华，等.USO－KBR测距系统建模与仿真［J］.航天器工程，2012，21（5）：91－95 Xin Ning，Qiu Lede，Zhang Lihua，et al.Modeling and simulation for USO－KBR ranging system［J］.Spacecraft Engineering，2012，21（5）：91－95（in Chinese）

［7］Kim J R.Simulation study of a low－low satellite－to－satellite tracking mission［D］.Austin：University of Texas at Austin，2000

［8］Furun Wang.Study on center of mass calibration and K－band ranging system calibration of the GRACE mission［D］.Austin：University of Texas at Austin，2003

［9］Flury J，Bettadpur S，Tapley B D.Precise accelerometry onboard the GRACE gravity field satellite mission［J］.Advances in Space Research，2008，42（8）：1414－1423

［10］Tapley B D，Ries J C，Bettadpur S，et al.Neutral density measurements from the gravity recovery and climate experiment accelerometers［J］.Journal of Spacecraft and Rockets，2007，44（6）：1220－1225

（编辑：夏光）

On－orbit Calibration Algorithm of Electrostatic Accelerometer for Gravity Measurement Satellite

XIN Ning1QIU Lede1ZHANG Lihua2LIU Naijin1
（1Institute of Telecommunication Satellite，China Academy of Space Technology，Beijing 100094，China）（2DFH Satellite Co.，Ltd.，Beijing 100094，China）

The electrostatic accelerometer is one of the most important instruments of the SST－LL（low－low satellite－satellite tracing）gravity measurement satellite which directly affects the measurement of the earth gravity field.In order to ensure long－term on－orbit working of electrostatic accelerometer and in combination with extended Kalman filter，a calibration algorithm based on dynamics is proposed for the accelerometer.Firstly，the observation model of the electrostatic accelerometer and KBR（K band ranging）system are obtained.Then，the accurate gravitational model and the measurements of electrostatic accelerometer are fitted into KBR－based extended Kalman algorithm.The associated simulation is performed to verify the availability and feasibility of the proposed calibration algorithm.The calibration accuracy of scale factors and biases can be better than 0.2%，which achieves the accurate calibration of satellite electrostatic accelerometer.

gravity measurement satellite；electrostatic accelerometer；K band ranging system；onorbit calibration

U666.1

：ADOI：10.3969／j.issn.1673－8748.2016.01.004

2015－03－26；

：2015－06－01

国家自然科学基金（91438205）资助项目

辛宁，男，博士，研究方向为卫星系统总体设计。Email：xinning7＠sina.com。