基于粮食产量灰色关联的生产模型实证分析
2016-04-24施丽娟
施丽娟,赵 晓,黄 凌
(福州外语外贸学院,福建福州 350202)
农业是中国的基础产业,粮食作为基础的核心,关系着中国的经济命脉。在“一带一路”和全球经济一体化发展背景下,中国能否充分利用国内国外两个市场两种资源,做大做强具有特色的优势产业,提升农业在全球的竞争力,最关键的是把握好粮食产量这一重要指标。因此,粮食产量的精确预测就能提高中国重要决策的准确度、加强国家的经济实力、提升国际地位。丁晨芳将指数平滑预测模型、多元线性回归预测模型、C-D生产函数模型加权组合得到预测模型来预测中国未来的粮食产量[1]。对于粮食产量波动大的问题,通过结合灰色系统和多元线性回归模型,给出了一种灰色多元线性回归模型提高预测精度[2-7]。马尔科夫理论在粮食产量预测中做了重要的贡献,通过马尔科夫模型的预测结果残差值进行相应的修正,以提高粮食产量的预测精度[8-9]。灰色关联理论可以对所有影响因子进行比较全面的定量分析,避免了主观因素对其造成的不确定性,本研究提出了灰色关联理论的生产模型,使得粮食产量的预测精度能够进一步提高。
影响粮食产量的因素较多,为了避免加工数据而引起的交互作用,导致对预测的影响。本研究选取了10个影响因素均为原始数据,分别为有效灌溉面积(X1)、农用化肥施用折纯量(X2)、农业机械总动力(X3)、成灾面积(X4)、受灾面积(X5)、农作物总播种面积(X6)、农林牧渔业从业人员(X7)、农用塑料薄膜使用量(X8)、农用柴油使用量(X9)、农药使用量(X10),而把粮食产量作为因变量用Y来表示。本研究选取了1995—2012年这18年的数据进行分析,数据来源于国家统计局、中国农业信息网、中国农业统计年鉴。
1 标准差标准化法
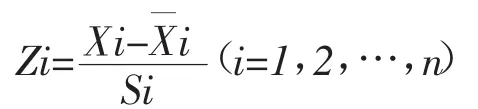
利用SPSS17.0对数据进行标准化处理,消除量纲影响,提高关联性的精确度,见表1。

表1 标准差标准化结果
2 灰色关联理论
灰色关联理论是在灰色系统基础上发展起来的,把关联度量化比较的一种新型方法。通过关联度的比较,可以在系统中找出主次因子,得到影响某因变量的主要因子,剔除次要因子,使得研究更有针对性,更接近事物的本质。
设粮食产量时间序列为:Y=(Y1,Y2,…,Ym)T,相应的第 i个影响因子的时间序列为:X=(X1i,X2i,…,Xmi)T(i=1,2,…,n),k时刻第i个影响因子时间序列对粮食产量时间序列的关联系数为:
其中,0<ρ≤1为分辨率,一般取ρ=0.5。各个时刻第i个影响因子的关联度为:
根据标准化后的数据进行灰色关联分析,求出粮食产量与各个影响因子之间的关联度,同时也给出关联度高低的排列序号,结果如表2所示。
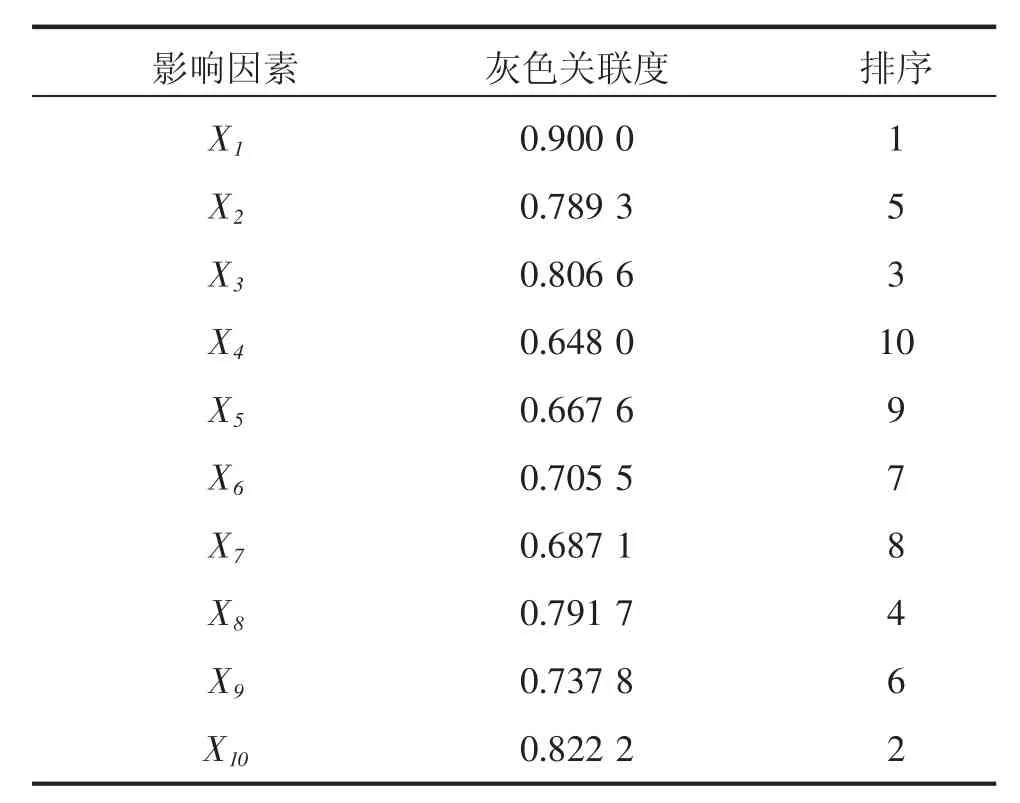
表2 灰色关联分析结果
从关联度分析表中可以看出标准化后数据关联度更高,显然有效灌溉面积的灰色关联度高达0.9000,排在所有影响因素的首位,与粮食产量最为密切,说明增加有效灌溉面积对粮食产量的提高具有显著性的影响。其次是农药使用量,增加农药的使用量虽然可以减少害虫对粮食的破坏,继而提高粮食产量,但是过高的使用农药有可能降低粮食的质量,破坏农业生态环境,建议适当增加农药使用量以提高粮食产量。仅次于农药使用量的影响因素为农业机械总动力,其灰色关联度为0.8066,农业机械总动力的大小标志着一个国家农业的现代化水平的高低,对粮食产量的影响又有突出的贡献,农业机械的使用不但能使粮食产量提高,更能使粮食的质量上升。因此,本研究选择灰色关联度大于0.75的5位影响因素:有效灌溉面积(X1)、农药使用量(X10)、农业机械总动力(X3)、农用塑料薄膜使用量(X8)、农用化肥施用折纯量(X2)作为粮食产量的影响因子建立模型。
3 生产模型建立
设有m组的观测数据,第j组的观测量如下,假设这m组的观测值满足以下关系式:
其中,β0,β1,β2,…,βn是 n+1 个待估计的参数,ε0,ε1,ε2,…εm是 m 个随机扰动项,相互独立且均值为 0,方差相同为 б2>0,服从(0,б2)分布,此模型为生产模型。
由灰色关联分析得到有效灌溉面积、农药使用量、农业机械总动力、农用塑料薄膜使用量、农用化肥施用折纯量这5个因子对粮食产量影响较其他因子显著,利用SPSS17.0对数据进行运行,结果见表3。
从表3可以得知在样本量为18个、置信度为95%的条件下,每一个回归系数均处于置信区间内,说明模型中的每一个自变量都是显著的,能有效的估计粮食产量。回归模型的判定系数高达0.9671,说明回归的拟合效果良好,并且自变量通过检验,参数值合理,模型能反映粮食产量18年来的变化规律,因此回归模型可以用于预测粮食产量,具体模型ln(Y)=-9.9993+1.6097ln (X1)+0.4153ln (X10)-0.9989ln(X3)-0.3508ln(X8)+2.0409ln(X2)。
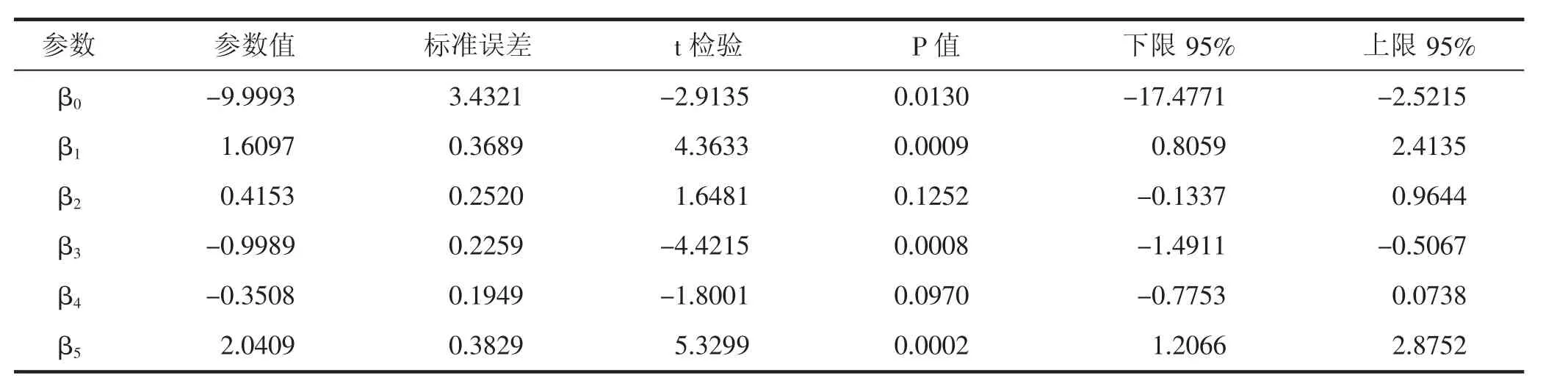
表3 参数估计值及检验
4 检验与结论
利用标准化消除数据之间的量纲关系,之后对数据进行灰色关联分析,从量上确定各影响因素与粮食产量之间的密切程度,于此得到有效灌溉面积、农药使用量、农业机械总动力、农用塑料薄膜使用量、农用化肥施用折纯量这5个影响因子作为模型的自变量。运用生产模型对1995—2012年这18年的数据进行回归处理得到模型,对此模型进行检验,通过误差相对数可体现出模型效果良好,能够较好的预测粮食产量见表4。粮食产量的波动性较大,受多种因素的影响,本研究利用标准化后的数据进行灰色关联分析剔除了相对比较稳定的因素,例如农作物播种面积、农林牧渔业从业人员等,得到的因子均是对粮食产量关系较密切的影响因素。检验结果表明,由对数回归而得的回归模型能较好的预测粮食产量。从模型可以看出,对粮食产量贡献最为明显的因子是有效灌溉面积,随着二氧化碳的排放增加,全球变暖,导致降水量的不均衡,增加灌溉面积,不仅能使得粮食产量的提高,而且能使生态环境得到改善。其次是农用化肥施用量,这就要求在使用化肥时,不仅要从量上有所增加,更应在质上提高,考虑氮、五氧化二磷、氧化钾的百分比。再者,农业机械总动力是一个国家农业现代化水平的重要指标,增加机械数量,加快农业技术改革,提高机械质量,使机械化水平更上一步。
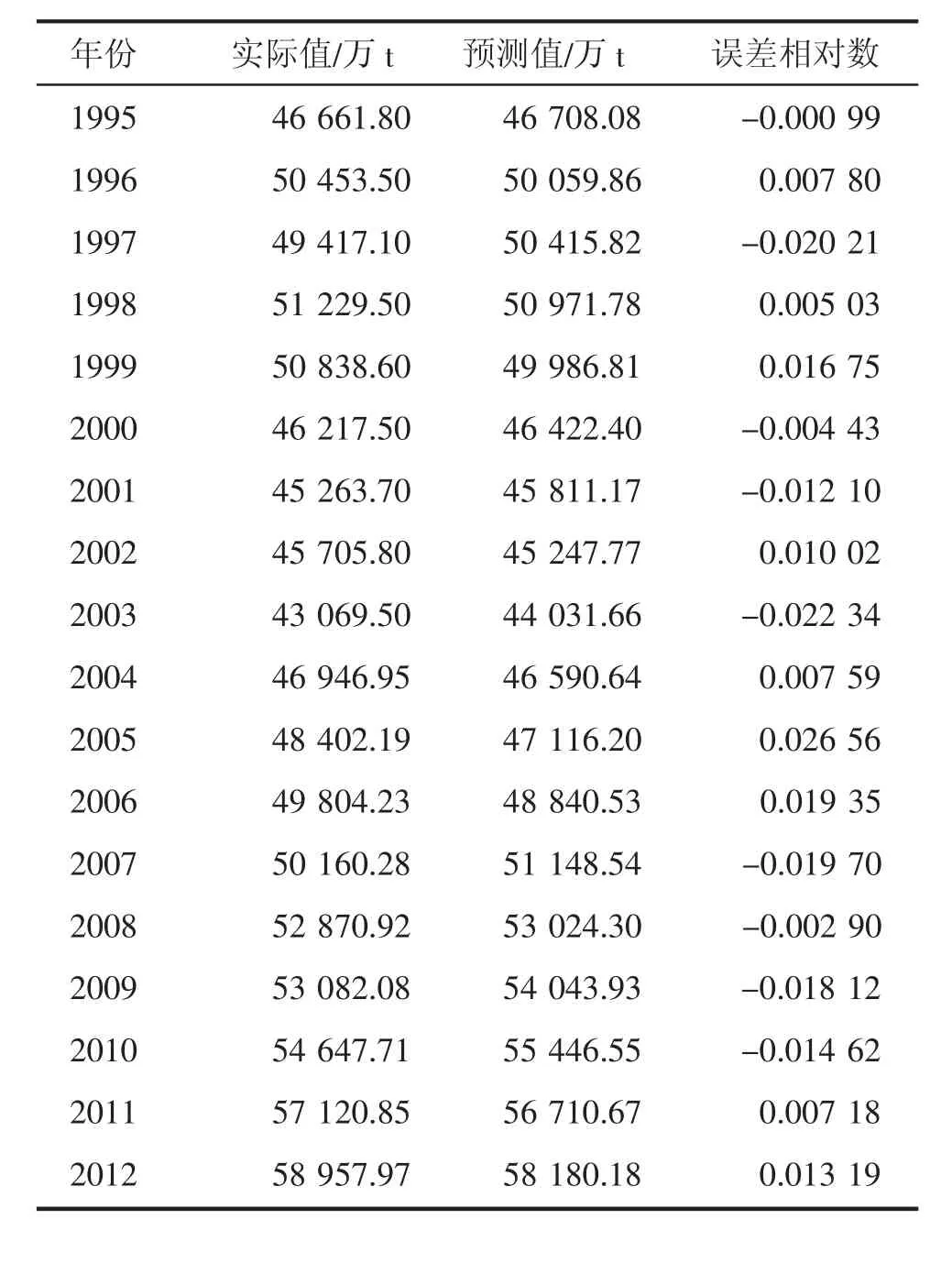
表4 实际值与预测值的比较
参考文献:
[1]丁晨芳.组合模型分析方法在我国粮食产量预测中的应用[J].农业现代化研究,2007,28(1):101-103.
[2]李军成,陈国华,石小芳.基于灰色多元线性回归的粮食产量预测[J].安徽农业科学,2010,38(16):8281-8282.
[3]苏 博,刘 鲁,杨方廷.GM(1.N)灰色系统与BP神经网络方法的粮食产量预测比较研究[J].中国农业大学学报,2006,11(4):99-104.
[4]胡晓丽,袁洪印,彭占武.灰色关联分析在吉林省粮食产量预测中的应用[J].农业与技术,2009,29(4):133-135.
[5]李炳军,李秋芳,卢秀霞.灰色线性回归组合模型在河南省粮食产量预测中的应用[J].河南农业科学,2009(10):44-47.
[6]宰松梅,温仵峰,谢成春.基于灰色关联分析的辽宁省粮食产量预测模型[J].节水灌溉,2011(5):64-66.
[7]林 芳.灰色神经网络在粮食产量预测中的应用[J].计算机仿真,2014,29(4):225-228.
[8]姚作芳,刘兴土,杨 飞.马尔科夫方法修正的灰色模型在吉林省粮食产量预测中的应用[J].地理科学,2010,30(3):452-457.
[9]向昌盛,张林峰.灰色理论和马尔可夫相融合的粮食产量预测模型[J].计算机科学,2013,40(2):245-248.
