基于进给速度自适应控制的NURBS曲线智能插补的新算法

谢斌,陈震,吕洪善

(亳州职业技术学院，安徽亳州236800)



基于进给速度自适应控制的NURBS曲线智能插补的新算法

谢斌,陈震,吕洪善

(亳州职业技术学院，安徽亳州236800)

摘要：通过对NURBS曲线的特点分析和NURBS曲线插补参数值求取方法的研究，在可控弦高误差算法的基础上，提出了一种简单而实用的NURBS曲线自适应插补算法。该算法充分考虑到机床的实际加工能力，对曲线段进行提前预插补，实现了加工进给速度自适应地随着曲率半径而变化，使加工运动更平滑，还避免了因加工曲线终点的判断而带来的复杂计算，并给出了快速求取插补点的3次 NURBS 曲线动态矩阵和曲线曲率的快速计算方法。

关键词：进给速度；NURBS曲线；弦误差；插值算法

0引言

对于一些高精度要求的复杂表面(如整体叶轮)，通常是通过研磨制造的。这些不可分割的整体零件加工需要高性能的数控系统，传统的加工方法是采用逐线性分段逼近的方法，将轮廓曲线分段进行研磨，此种加工方法效率低，导致表面加工质量差。

随着先进数控系统的研制成功和计算机计算速度的提高，在 CAD系统中生成由NURBS曲线构成自由曲面，可直接进行加工。要实现这种方法则需要解决以下问题：一是分段直线逼近会产生大量NC代码数据的记忆和传输；二是零件表面质量误差的控制[1-3]。

除了在起始和结束点外,简单的插值算法是速度保持不变，弦误差随曲线曲率变化而变化，加工精度很难保证。要想控制弦误差必须控制速度变化以及曲线的曲率变化。而机床的切向和法向加速度是由机电系统容量限制的,故速度不能迅速下降到弦高误差的规定范围内,并且弦误差随截面曲线的曲率变化非常大。此外，满足所需弦误差的机床可能不能满足正常加速度曲率半径很小的瞬时速度。基于控制弦误差的插补算法，提出了一种自适应速度控制的智能算法。根据机床的实际加工能力，该算法采用超前分析最大减速距离所要求截面曲线的方法，无需对NURBS曲线结束点估计进行复杂计算。因此，进给速度可提前降低到与曲率制作加工运动比较平稳的变化值。

1实时自适应插值的三维样条曲线

1.1NURBS 定义

NURBS曲线向量值有理多项式的形式定义

(1)

式中：di是控制点,i= 0,1,…,n；wi是权重，i = 0,1,…,n；Ni,k(u)是以下符号化的归一K阶B样条基函数。

(2)

1.2控弦误差插补[4-5]算法

相对于t 参数u的函数表示为 u(ti)= ui，u(ti+1)=ui+1，利用泰勒展开，近似到二阶导数

(3)

速度的定义为

(4)

定义采样时间间隔TS=Ti+1-Ti，然后一阶插值算法，式(4)代入式(3)，并忽略高阶项，式(3)可以处理为

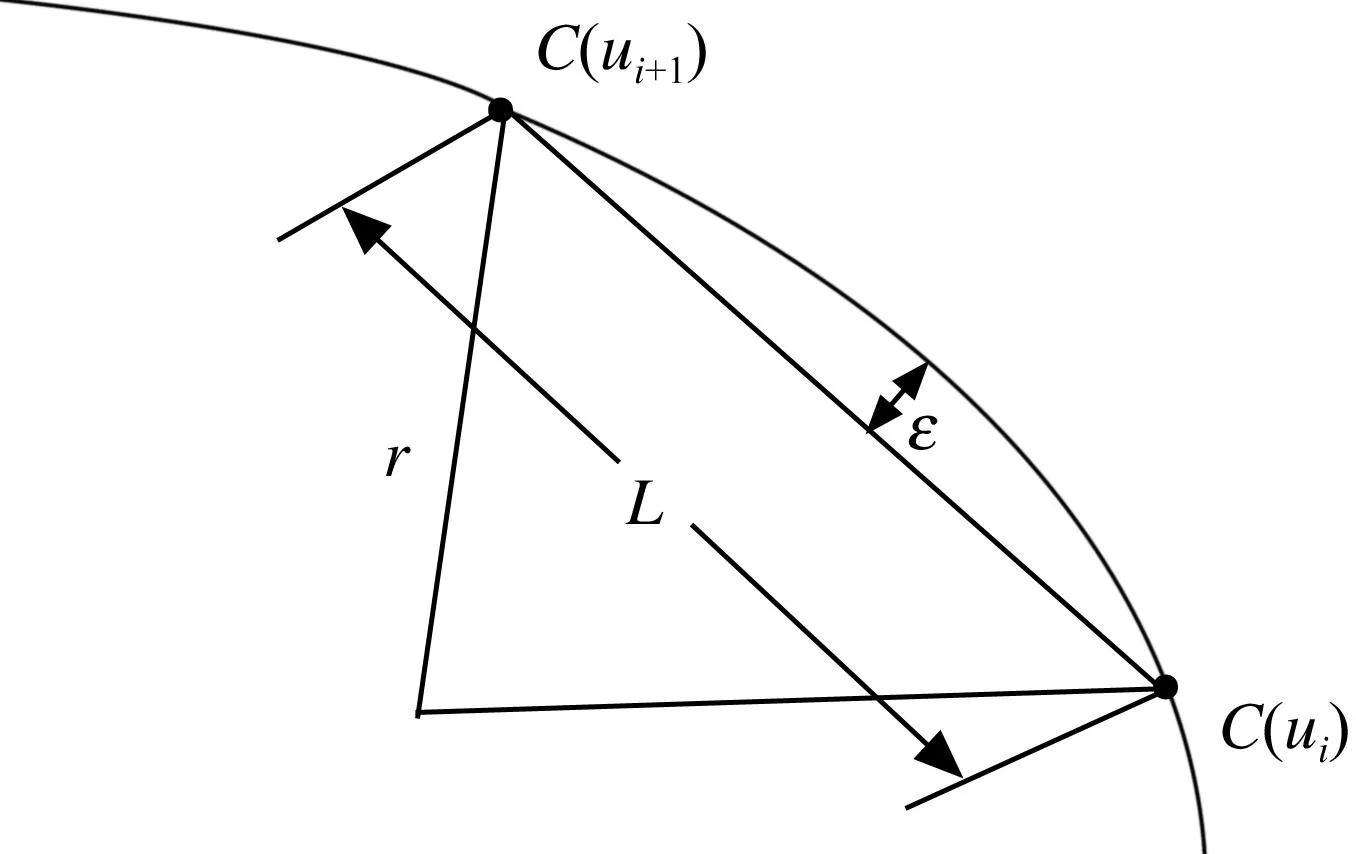
图1　估计下插值点

假如u∈[ ui，ui+ 1]是由圆弧近似(如图1所示)，其中当参数u =ui时，r为曲率半径，当u = ui，u=ui+1时，C(ui)和C(ui+1)是插值曲线上的点。

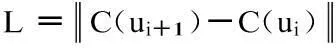
由此产生弦误差

得到的V(ui)在ε弦误差函数为

(5)

如果ε弦高误差和采样时间TS不变，V(ui)跟随曲率半径r的变化,而机床的切线和正加速度是由机电系统的容量限制的。因此，在规定范围内曲线段的曲率，所需正常加速度引起的弦误差非常大，将超过允许值αNmax，以及在规定范围内曲线部分的曲率变化率，所需的切向加速度，会使弦误差变大，将超过允许值最大αmax，所以机床的机械特性时必须考虑进给速度自适应调整。因此，下面介绍进给速度调整的自适应算法。

1.3正常加速插值算法

正常加速度与进给速度V(ui)、曲线的曲率半径r之间的关系[6]可表示为

最大允许的速度是

(6)

自适应调整进给速度为

(7)

在曲线部分曲率变化率非常大的地方实际切向加速度可能不满足调整进给速度计算(式(7))，这意味着速度不能下降，在短时间内有可能导致过切现象。这些问题可以通过以下的算法来解决。

1.4控制切线加速度插值算法

给定最大加速度αmax，相应的进给速度是Vmax。如果实际情况以αmax进行减速，从速度Vmax到0的减速距离sm为

因此，多种采样插值曲线必须提前分析以确保这些采样插补段总长度至少等于sm。只有这样，当前的加工段才不受后采样差值段速度平滑性的影响。

图2　线段轨道

如图2所示，假设每个取样长度内插段为S0，S1，…，Sj，将进给速度定义为V0，V1，…，Vj，Vj + 1。

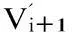
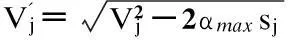
(8)

否则，V2将会极力影响到接下来的速度分析。

当u=1时到达曲线的终点，速度必须降低到V = 0，同样必须利用式(8)进行调整。显然，该算法避免对加工曲线结束点估计的需要。在文献[7]，对大量的曲线长度进行动态计算会受曲线实时响应结束点估计的影响。

2动态矩阵表示NURBS曲线

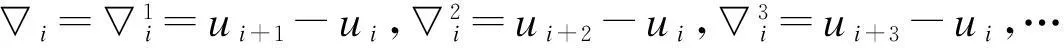
当t∈〔0,1〕，定义t=(u-ui)/(ui+1-ui)=(u-ui)/▽i。

如果NURBS曲线是第3阶(k=3)，则曲线与截面可以用矩阵表示为

式中0≤t≤1，i = 3，4，…，n。

扩展这个矩阵的每个术语，并定义

a=m11wi-3di-3+m12wi-2di-2+m13wi-1di-1+m14widi

b=m21wi-3di-3+m22wi-2di-2+m23wi-1di-1+m24widi

c=m31wi-3di-3+m32wi-2di-2+m33wi-1di-1+m34widi

e=m41wi-3di-3+m42wi-2di-2+m43wi-1di-1+m44widi

a1=m11wi-3+m12wi-2+m13wi-1+m14wi

b1=m21wi-3+m22wi-2+m23wi-1+m24wi

c1=m31wi-3+m32wi-2+m33wi-1+m34wi

e1=m41wi-3+m42wi-2+m43wi-1+m44wi

然后

假定控制点的di和权重wi是已知的，Mi是节点矢量u仅有相关矩阵并可以在曲线与截面的插值计算得到。

因此，在插值当中只有参数t的增量△t需要计算，这就大大提高了计算速度。

3算法的软件实现

在曲线的起始部分，分别应用梯形或S形曲线的加速方法和算法。比较了2种方法所计算的速度，采用了最小速度，并将所提出的算法单独应用要比前者速度快。

为了避免花太多由式(8)调整进给速度的时间，在这一过程中，要求对方根进行频繁而繁琐的计算，进给速度的平方是被记忆的不同于预插段的进给速度，进给速度的调整可以按以下方程处理。

(9)

当按照进给速度的平方计算平方根进行插补段的加工时，对每一段的进给率调整是1个只有4次加法或减法处理(2αmax可以被视为1个参数)。

在递归计算过程，直到插补段被加工，只是速度值改变，而其他保持不变。当前的预插值点是被实际插值点代替(如图3所示)，第1、第4和第6点是按弦误差和最大进给速度预先计算的，第2、第3和第5是按控制切向、法向加速度实际计算得插值点。

因为任意相邻的2个预插值点之间的速度必须满足以下不等式

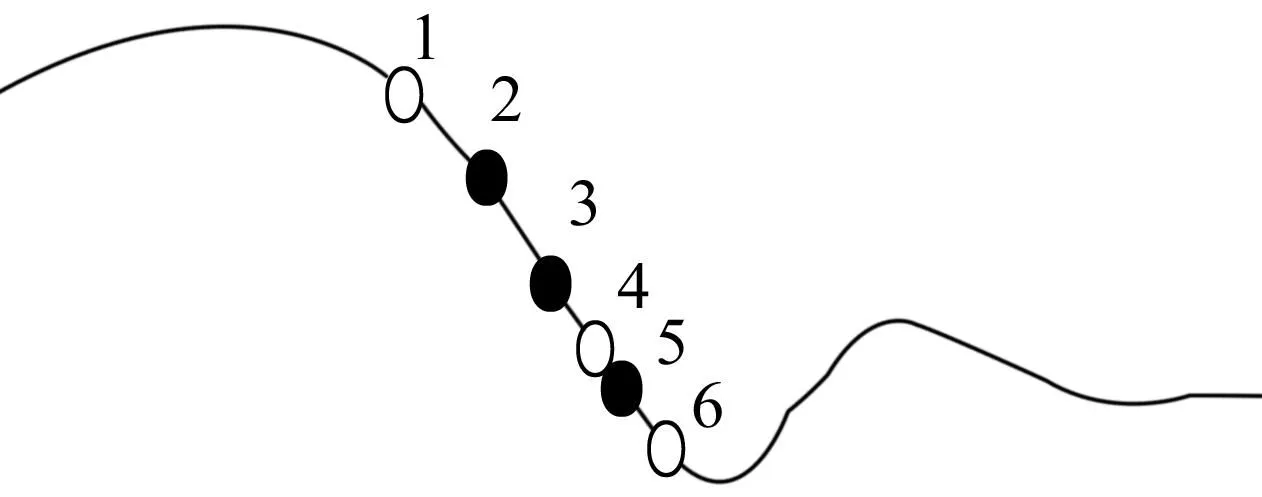
图3　NURBS曲线插值点

任意相邻的2个实际插值点之间的速度也必须满足上述要求。

第2、第3和第5点进给速度可以由以下式得出，即

V2=(V1+V4)/2

V3=(V2+V4)/2

V5=(V4+V6)/2

最后，计算了参数的增量值和实际插值点。

4实验

为了验证提出的方法，整个过程是由基于DSP运动控制卡完成的。工艺参数分别如下：最大进给速度为6 m/min；起始速度为0.5 m/min；在进给方向的最大加速度9.8 m2/ s；法向加速度为0.98 m2/s；插补时间间隔TS为2 ms；刀具半径为3 mm；轮廓误差是2 μm。

图4显示了NURBS曲线及其控制点，图5显示了它的曲率半径。

在某些领域，加速或减速超过给定值如图6所示。

调整后的插值算法控制切向、法向加速度如图7所示，进给速度和进给加减速度的变化都在数控系统参数的范围内。

图8为加工NURBS曲面，图9为加工NURBS曲面的横截面。

图4　NURBS曲线控制点

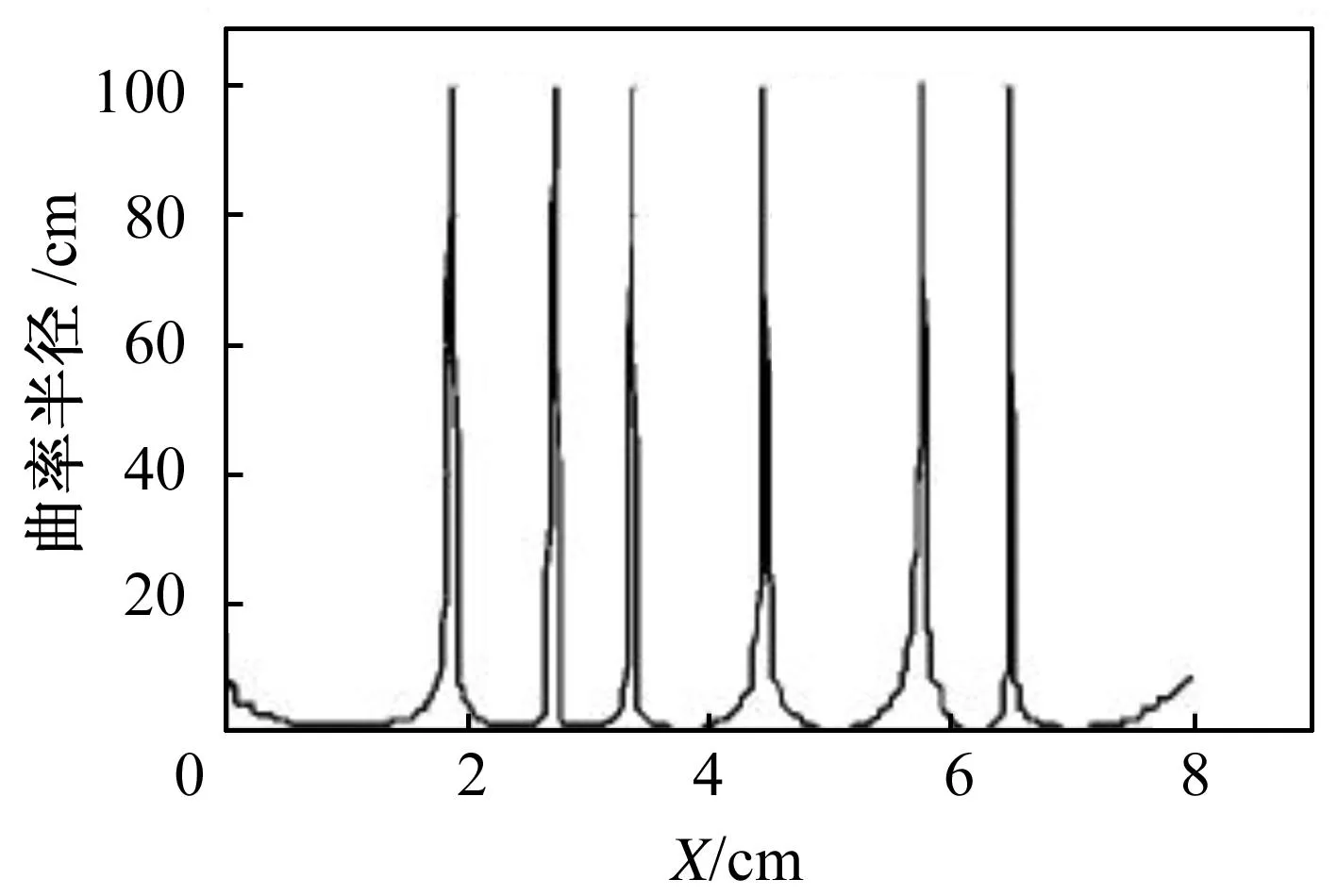
图5　NURBS曲线的曲率半径

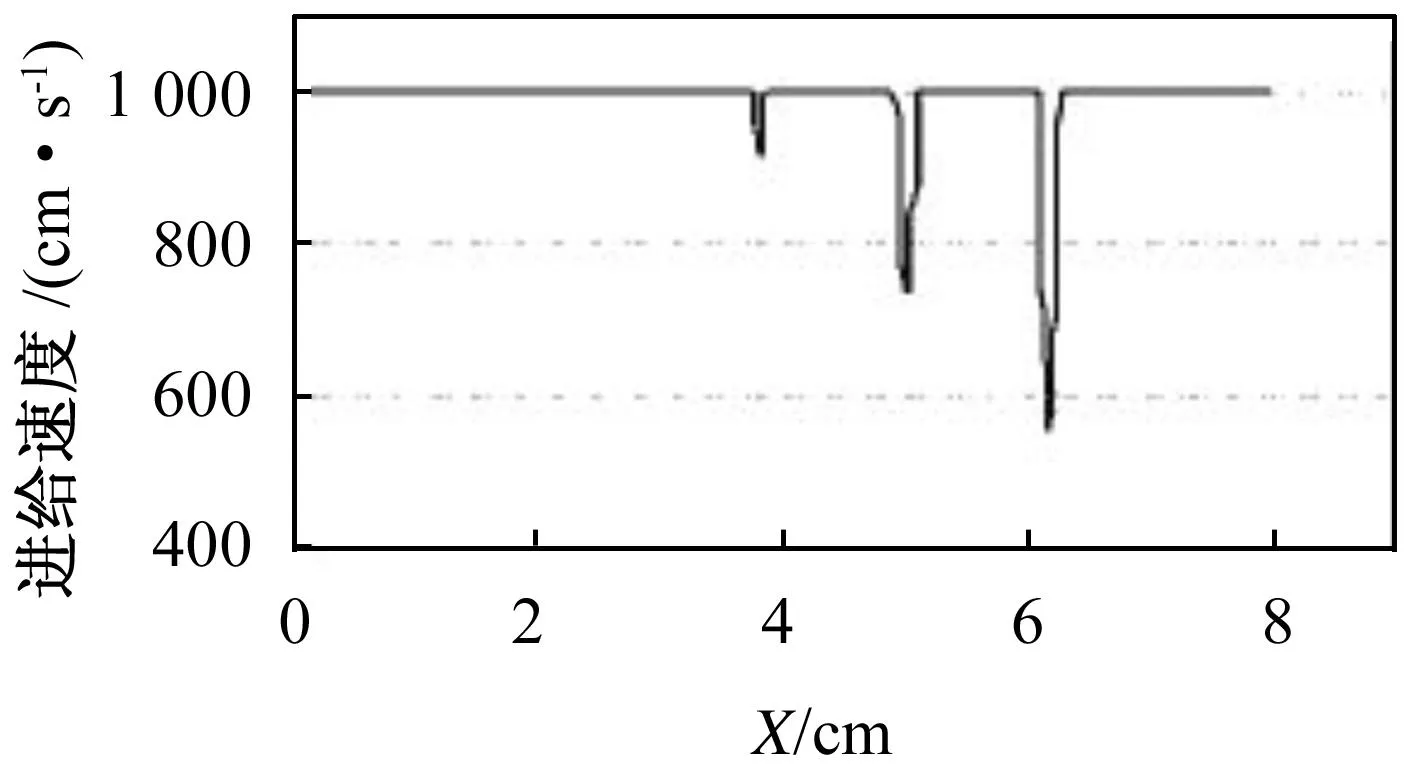
图6　控弦误差插补算法调整后的进给速度

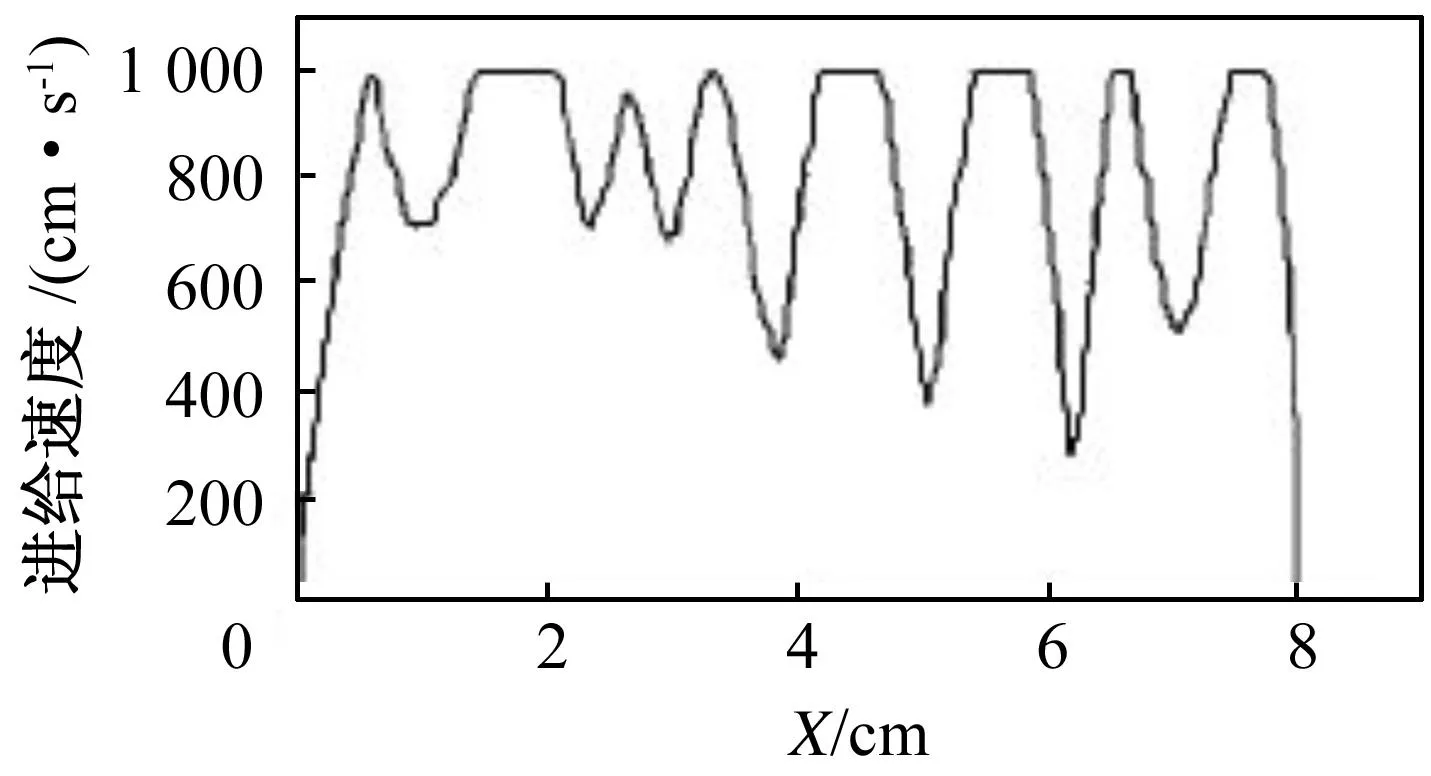
图7　速度调整后切线和法线加速度控制

图8　NURBS曲面的加工

图9　加工曲面的截面

5结论

NURBS曲线插补对于高速、高精度加工系统的重要性已经备受关注。尽管按所提出的算法花费的时间远远超过了由恒定进给率算法的时间，但却具有如下优点：①充分考虑了机床的实际容量；②能够控制轮廓误差；③使机器工具的运动相当平稳；④改善了工件表面质量。

[参考文献]

[1]CHENG M Y,TSAI M C,KUO J C.Real-time NURBS command generators for CNC servo controllers[J].International Journal of Machine Tools and Manufacture,2002,42(7):801-803.

[2]LARTIGUE C,THIEBAUT F,MAEKAWA T.CNC tool path in terms of B-spline curves[J].Computer-Aided Design,2001,33(4):307-319.

[3]BAHR B,XIAO X,KRISHNA K.A real-time scheme of cubic parametric curve interpolations for CNC systems[J].Computers in Industry,2001,45(3):309-317.

[4]YEH S S,HSU P L.Adaptive-feedrate interpolation for parametric curves with a confined chord error[J].Computer-Aided Design,2002,34(3):229-237.

[5]FAROUKI R T,TSAI Y F.Exact Taylor series coefficient for variable feedrate CNC curve interpolators[J].Computer-Aided Design,2001,33(2):155-165.

[6]FAROUKI R,MANJUNATHAIAH J,NICHOLAS D,et al.Variable-feedrate CNC interpolators for constant material removal rates along Pythagorean-hodograph curves[J].Computer-Aided Design,1998,30 (8):631-640.

[7]KRISHNAN K K,KAPPEN J,BAHR B.Calculation of variable federate and spindle speed for NURBS based CNC machining[J].Transactions of NAMRI/SME,2001,24:429-435.

责任编辑：陈亮

A New Intelligent Interpolation Algorithm for NURBS Curve Based on Adaptive Control of Feed Rate

XIE Bin，CHEN Zhen，LYU Hongshan

(Bozhou Vocational and Technical College,Bozhou 236800)

Abstract：Based on the calculation method of characteristic analysis and NURBS curve interpolation parameters on the NURBS curve and the controllable chord error algorithm,the article proposed a simple and practical self-adaptive interpolation algorithm for NURBS curve.The algorithm fully took into account the actual machining ability of curve by pre interpolation,and according to the maximum number of interpolation cycle for pre interpolation deceleration,the feed speed could slow down in advance and make machining feed rate adaptively change with the radius of curvature change rate,which made the machining movement more smooth and avoided the complex calculation required of determining the endpoint of curve.At last,the article gave a fast calculation method for computing three NURBS curve of dynamic matrix representation of interpolation points and curvature.

Key words：feed rate;NURBS curve;string error;interpolation algorithm

中图分类号：TG659

文献标志码：A

文章编号：1671- 0436(2016)01- 0025- 06

作者简介：谢斌(1973—)，男，硕士，讲师。

基金项目：安徽省教育厅高等学校省级质量工程项目(2013jyxm372，2013zy177)；安徽省教育厅、财政厅高校省级自然科学研究项目(KJ2014A170)

收稿日期：2015-12-30

doi:10.3969/j.issn.1671-0436.2016.01.006