“微波技术基础”课程中的增量电感法

吴林晟， 唐　旻， 毛军发

(上海交通大学 电子信息与电气工程学院， 上海 200240)



“微波技术基础”课程中的增量电感法

吴林晟， 唐旻， 毛军发

(上海交通大学 电子信息与电气工程学院， 上海 200240)

摘要：衰减常数是微波传输线的重要特性参数。精确计算传输线的导体损耗衰减常数需要分析特定模式的电磁场并在导体表面积分。增量电感法将TEM或准TEM模导体损耗衰减常数的计算等效为特性阻抗对几何尺寸的偏导问题，简化分析过程。本文以同轴、带状线、微带线为例，阐述了增量电感法的原理、应用方法、适用范围，并加以讨论。

关键词：增量电感法；传输线；导体损耗

0引言

传输线传播常数的实部称为衰减常数α，表示本征模式沿导波结构传播过程中其模式电压和电流幅度在单位长度内的衰减，是传输线的重要特性参数之一。传播模式下传输线的衰减主要由导体损耗、介质损耗和辐射损耗等因素引起。其中，辐射损耗一般控制在较小的范围内，在分析中可忽略[1]。介质损耗衰减常数αd由介质基板相对介电

常数、损耗角正切、模式的相位常数及其对应的自由空间波数所决定，计算公式相对简单[2]。而导体损耗衰减常数αc则涉及到传输线导体表面损耗密度的积分，与传输线横截面结构密切相关，计算也相对复杂。

为此，研究者们提出多种计算传输线导体损耗衰减常数的方法，如分布参数法、微扰法和增量电感法等[3]。其中，增量电感法仅需知道传输线特性阻抗与其横截面几何尺寸间关系及导体表面电

阻即可估计传输线横电磁(TEM)模或准TEM模导体损耗衰减常数，使用便捷，得到广泛应用[4]。

本文将具体论述增量电感法的原理和应用范围，导出几种典型导波结构中TEM或准TEM模的导体损耗衰减常数并加以讨论，供教学时参考。

1增量电感法

增量电感法最初由文献[5]提出，该法利用了导体损耗与导体内部磁场储能公式的高度相似性，并且和微扰法一样也基于微小扰动的前提，即传输线上的损耗足够小以至于有耗传输线的电磁场分布与无耗情况下基本一致。

1.1增量电感和分布电阻

传输线TEM模的分布电感定义与单位长度内的磁场储能有关，即[3]

(1)

其中Ht为横向磁场，I0为模式电流，μ为磁导率，S表示横截面。对良导体构成的导波结构，部分电磁场会进入导体内部。由此，L可分为原电感L0(导体之间磁场贡献的电感)和增量电感ΔL(导体内磁场贡献的电感)。增量电感ΔL为

(2)

其中Hs为导体表面切向磁场，t和δs为导体厚度和趋肤深度，C表示导体表面，n是导体表面内法线方向变量。式(2)后一个积分项源于良导体中平面波按指数衰减，良导体内电磁波衰减常数为1/δs的事实，当t>>δs时该积分趋于δs/2。式(2)可化为

(3)

其中Rs=1/σδs为导体表面电阻，ω为角频率。通常δs远小于导波结构特征尺寸，式(3)视为所有导体表面缩进δs/2时分布电感变化量，由一阶近似得

(4)

与导体损耗相关的传输线分布电阻为[3]

(5)

其中Js为导体表面电流密度。由此可得如下关系：

R=ωΔL

(6)

式(6)表明单位长度增量电感的电抗值刚好等于分布电阻值，这是由于进入导体内部的磁场在提供额外磁场储能的同时也引入了导体损耗。而且，良导体中平面波的相位常数与衰减常数相等，当导体足够厚时良导体的表面阻抗Zs的实部即表面电阻Rs和虚部即表面电抗Xs相等，该表面电抗是良导体内额外磁场储能和增量电感的一种体现。

1.2导体损耗衰减常数

可定义导波结构中TEM或准TEM模的特性阻抗Z0。导体损耗衰减常数可由分布参数法得到

αc=R/2Z0

(7)

将式(4)和(6)代入式(7)得

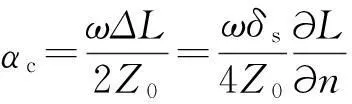
(8)

注意，导体损耗主要与磁场储能的变化量相关联。

增量电感的影响可进一步体现为特性阻抗的增量。空气填充导波结构的特性阻抗为

(9)

其中v0为空气中光速，显然与导体损耗引起的磁场变化无关。代入式(8)并化简得到

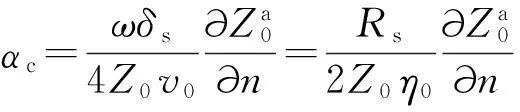
(10)

其中η0是空气的本征阻抗。对于均匀填充相对介电常数为εr介质的导波结构，有

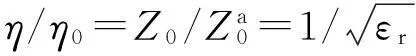
(11)

式(10)变换为[3]

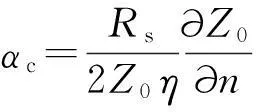
(12)

其中η是媒质的本征阻抗。

2应用实例与讨论

通过上述推导可知，利用增量电感法可将导波结构中TEM模或准TEM模的导体损耗衰减常数问题转化为特性阻抗关于结构几何尺寸的偏导问题。已知特性阻抗与几何尺寸的解析关系时，可避免对特定模式的电磁场进行积分，计算过程大为简化。文献[5]严格推导了增量电感法的结论，并提出特性阻抗微扰法，推广到TM模的分析。

下面以3种常见导波结构为例，对导体损耗衰减常数增量电感法的应用进行具体说明。

2.1同轴线中的TEM模

图1所示为同轴线的横截面，其中a为内导体的半径，b为外导体内径，εr为填充介质的相对介电常数，对于空气填充同轴线有εr=1。严格求解TEM模标量电位Φ满足的横向Laplace方程，容易得到其电磁场分布，根据唯一定义的模式电压V和模式电流I得到TEM模的特性阻抗为

(13)

图1　同轴线的横截面

由式(13)可以发现，特性阻抗与a、b两个几何尺寸有关。又如图1所示，当金属表面缩进小量Δ=δs/2时，a减小Δ，b增加Δ。由此，式(12)对同轴线TEM模导体损耗衰减常数表现为

(14)

将式(13)代入可得下式：

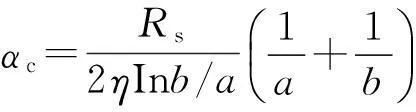
(15)

这与分布参数法、微扰法得到的结果完全一致[3]。由于式(13)中特性阻抗是严格推导的结果，基于其偏导的增量电感法得到的也是严格的结果。

2.2带状线中的TEM模

图2所示为均匀填充对称带状线的横截面，其中W和t分别为导带宽度和厚度，b为上下金属板间距，εr为基板相对介电常数。该导波结构可以传输TEM模，可利用保角变换严格求解导带厚度为0时的电磁场分布，但对于有限金属厚度的场景要严格求解则较为困难。

图2　带状线的横截面

文献[5]给出一组经验公式近似表征带状线TEM模的特性阻抗。对窄薄导带情况即W/(b-t)<0.35，t/b<0.25且t/W<0.11时，有

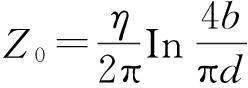
(16)

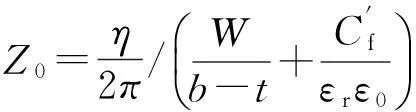
(17)

如图2所示，当金属表面缩进Δ时，W和t均减小2Δ，b增加2Δ。由此，式(12)对带状线TEM模导体损耗衰减常数表现为

(18)

针对窄薄导带和宽导带两种情况，分别将式(16)和(17)代入式(18)，可以得到其导体损耗衰减常数的近似公式。本文省去推导过程，仅给出最终结果[6]。当W/(b-t)<0.35，t/b<0.25且t/W<0.11时，

(19)

当W/(b-t)>0.35时，

(20)

式(19)和(20)是用不同参数范围的特性阻抗近似计算得到的。虽然特性阻抗的拟合误差较小，但基于偏导的导体损耗衰减常数误差会被放大。如图3上部一根曲线所示，两式在W/(b-t)=0.35处的结果不连续(虚线)，可在其中间插值(实线)近似。

图3　带状线和微带线导体损耗衰减常数计算结果

2.3微带线的准TEM模

图4所示为微带线的横截面，其中W和t分别为导带宽度和厚度，h和εr为基板厚度和相对介电常数，方块标记1～5分别表示导带顶面、底面、左侧、右侧和地面。微带线主模是准TEM模，工作频率较低时可仿照TEM模用准静态分析并定义其特性阻抗(常用功率/电流定义)，有近似公式[1]：

Z0=

(21)

其中εre为有效相对介质常数[1]。应用式(10)可得

(22)

式(22)中标记1～5表示不同导体表面以及地面上的部分损耗，每项均对应该导体表面内缩时引起的特性阻抗变9化，导带底面损耗同时与对h和t的偏导有关。

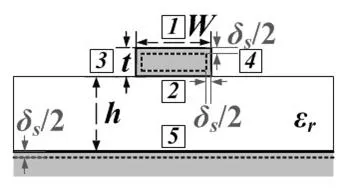
图4　微带线的横截面

将式(21)代入式(22)得微带线导体损耗衰减常数近似公式[1]：

(23)

式(23)也是根据几何参数范围分段计算的，如图3所示结果也存在不连续，需对其进行插值处理。同时应注意，微带线的准TEM模在高频时存在色散，准静态分析将失效。由此，式(23)只能用于较低频段，可忽略色散效应的频率范围参见文献[2]。

此外，工程上经常对微带线表面进行处理，如镍金、镀银等，为增加导体与基板界面的结合力也会有意引入粗糙度，这都会不同程度地改变导体的等效表面电阻。此时，式(22)写为

(24)

其中Rsi(i=1～5)为导体表面i的等效电阻。

3结语

本文分析了用于计算传输线TEM或准TEM模导体损耗衰减常数的增量电感法，将特定模式导体损耗的电磁场分析转化为特性阻抗对几何尺寸的偏导问题，简化计算过程。通过同轴线、带状线、微带线等应用实例，表明该方法不仅适用于TEM金属波导，也可用于平面传输线的分析。

参考文献:

[1]I. J. Bahl, R. Garg, M. Bozzi. Microstrip Lines and Slotlines, 3rd ed.[M]. Boston, USA: Artech House, 2013.4

[2]周希朗. 微波技术与天线[M]. 南京: 东南大学出版社, 2009年8月

[3]D. M. Pozar. Microwave Engineering, 4th ed.[M]. New York, USA: John Wiley & Sons, 2011.11

[4]梁昌洪, 谢拥军, 官伯然. 简明微波[M]. 北京: 高等教育出版社, 2006年7月

[5]H. A. Wheeler. Formulas for the skin effect [J]. USA: Proceedings of the IRE, 1942, 30(9):412-424

[6]S. B. Cohn, Problems in strip transmission line [J]. USA: IRE Trans. Microw. Theory Tech., 1955, 3(2): 119-126

Incremental Inductance Method in Fundamentals of Microwave Technology Course

WU Lin-sheng, TANG Min, MAO Jun-fa

(SchoolofElectronicInformationandElectricalEngineering,ShanghaiJiaoTongUniversity,Shanghai200240,China)

Abstract:The attenuation constant is an important characteristic parameter of a microwave transmission line. In order to accurately calculate the attenuation constant due to conductor loss, the analysis of electromagnetic fields modal and the integration on conductor surfaces are required. The incremental inductance method can significantly simplify the analysis by transforming the field calculation to the partial differential of characteristic impedance to the geometric parameters. With the examples of coaxial line, stripline and microstrip line, this paper explains the principle of incremental inductance method and discusses its applications and corresponding applicable scopes.

Keywords:incremental inductance method; transmission line; conductor loss

文献标识码：A

文章编号：1008-0686(2016)01-0049-04

中图分类号：G423.07;TN015

作者简介：吴林晟(1981-)，男，博士，副教授，主要从事电磁场与微波技术教学、射频与微波电路科研工作，E-mail：wallish@sjtu.edu.cn唐旻(1980-)，男，博士，副教授，主要从事电磁场与微波技术教学、高速电路科研工作，E-mail：tm222@sjtu.edu.cn毛军发(1965-)，男，博士，教授，主要从事电磁场与微波技术、射频系统级封装研究工作，E-mail：jfmao@sjtu.edu.cn

收稿日期:2015-04-28;修回日期:2015-09-18