三次有理Bézier曲线与HC-Bézier曲线的拼接
2016-04-22张丹丹吴欢欢
张丹丹, 吴欢欢
(安徽广播电视大学 安庆分校, 安徽 安庆 246001)
三次有理Bézier曲线与HC-Bézier曲线的拼接
张丹丹, 吴欢欢
(安徽广播电视大学 安庆分校, 安徽 安庆246001)
摘要:讨论了三次有理Bézier曲线与带一个形状参数的HC-Bézier曲线的光滑拼接问题,并给出了三次有理Bézier曲线与HC-Bézier曲线的G0、G1和G2光滑拼接的几何条件.
关键词:有理Bézier曲线;HC-Bézier曲线;形状参数;拼接条件
0引言
随着几何造型工业的发展,原有的Bézier曲线[1]的方法已难以满足人们对几何造型的需求,于是科研人员开始对带形状参数的Bézier曲线、曲面及它们间的光滑拼接问题进行研究.例如,胡钢等[2]构造了带多形状参数的三次扩展Bézier曲线,并给出了曲线间的G1、G2和C1、C2拼接条件;杨林英等[3]讨论了λαβ-Bézier曲线与三次Bézier曲线的拼接;孙洁保等[4]分析了TC-Bézier曲线及其曲线间的拼接条件;苏本跃等[5]在双曲函数空间中提出了双曲多项式曲线HC-Bézier曲线.在此基础上,本研究分析了三次有理Bézier曲线与带一个形状参数的HC-Bézier曲线的光滑拼接问题,并讨论了这2条曲线间的G0、G1和G2光滑拼接的几何条件.
1有理Bézier曲线的定义
设控制顶点为Q0、Q1、Q2、Q3,三次有理Bézier曲线P(u)为,
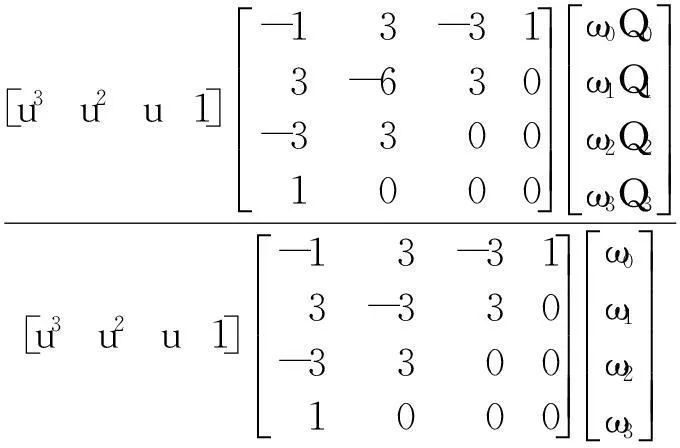
u=[0,1],
式中,ωi(i=0,1,2,3)为对应控制顶点的权因子,且ωi>0(i=0,1,2,3).
三次有理Bézier曲线端点及端点切矢为,
P(0)=Q0,P(1)=Q3;
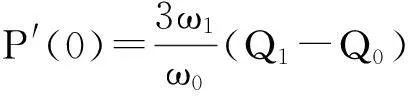

2HC-Bézier曲线的定义
设控制顶点为V0、V1、V2、V3,α是任意实数,且α>0,则曲线,
称为三次HC-Bézier曲线.
令,β=1-cosh(α-t),γ=1-cosht,那么,
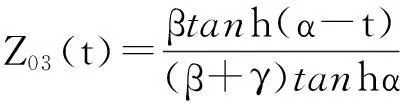
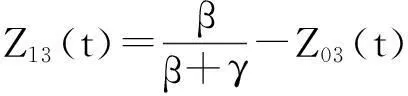
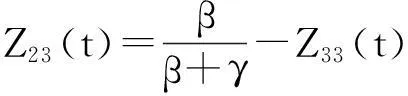

三次HC-Bézier曲线端点及端点切矢为,
R(0)=V0,R(1)=V1;
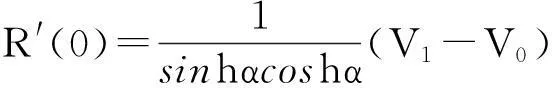
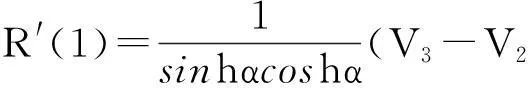
3Bézier曲线与HC-Bézier曲线的拼接条件
3.1G0光滑拼接
定理1三次有理Bézier曲线P(u)与三次HC-Bézier曲线R(t)的G0光滑拼接的充要条件是,Q3=V0.
证明两曲线P(u)与R(t)的G0光滑拼接的充要条件是P(u)与R(t)具有公共连接点,即P(1)=R(0).
因为,P(1)=Q3,R(0)=V0.
所以,Q3=V0为三次有理Bézier曲线P(u)与三次HC-Bézier曲线R(t)的G0光滑拼接的充要条件,见图1.
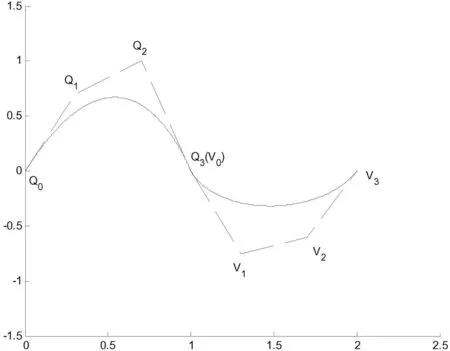
图1有理Bézier曲线与HC-Bézier曲线的光滑拼接
3.2G1光滑拼接
定理2三次有理Bézier曲线与三次HC-Bézier曲线的光滑拼接的充要条件是:
1)Q3=V0;
2)存在δ>0,使得,
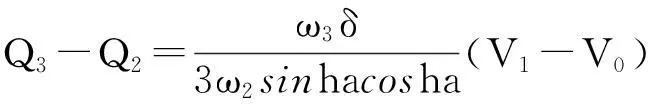
则曲线P(u)与曲线R(t)在公共连接点处G1光滑拼接.
证明两曲线P(u)与R(t)在公共连接点处G1光滑拼接的充要条件首先是满足G0条件,其次是两曲线在公共连接点处具有公共的切矢方向.
1)G0光滑连接,已由定理1证明.
2)只需证明存在δ>0,使得,
P′(1)=δR′(0).
因为,
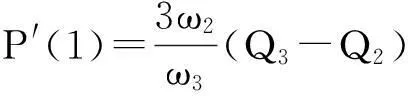
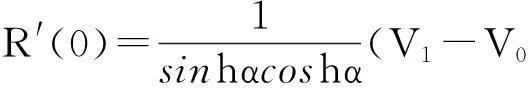
由条件2)知,存在δ>0,使得,
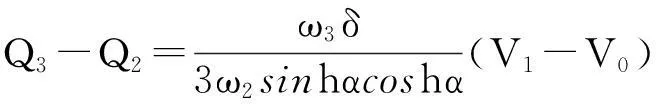
所以,
P′(1)=δR′(0).
则两曲线P(u)与R(t)在公共连接点处G1光滑拼接,见图2.
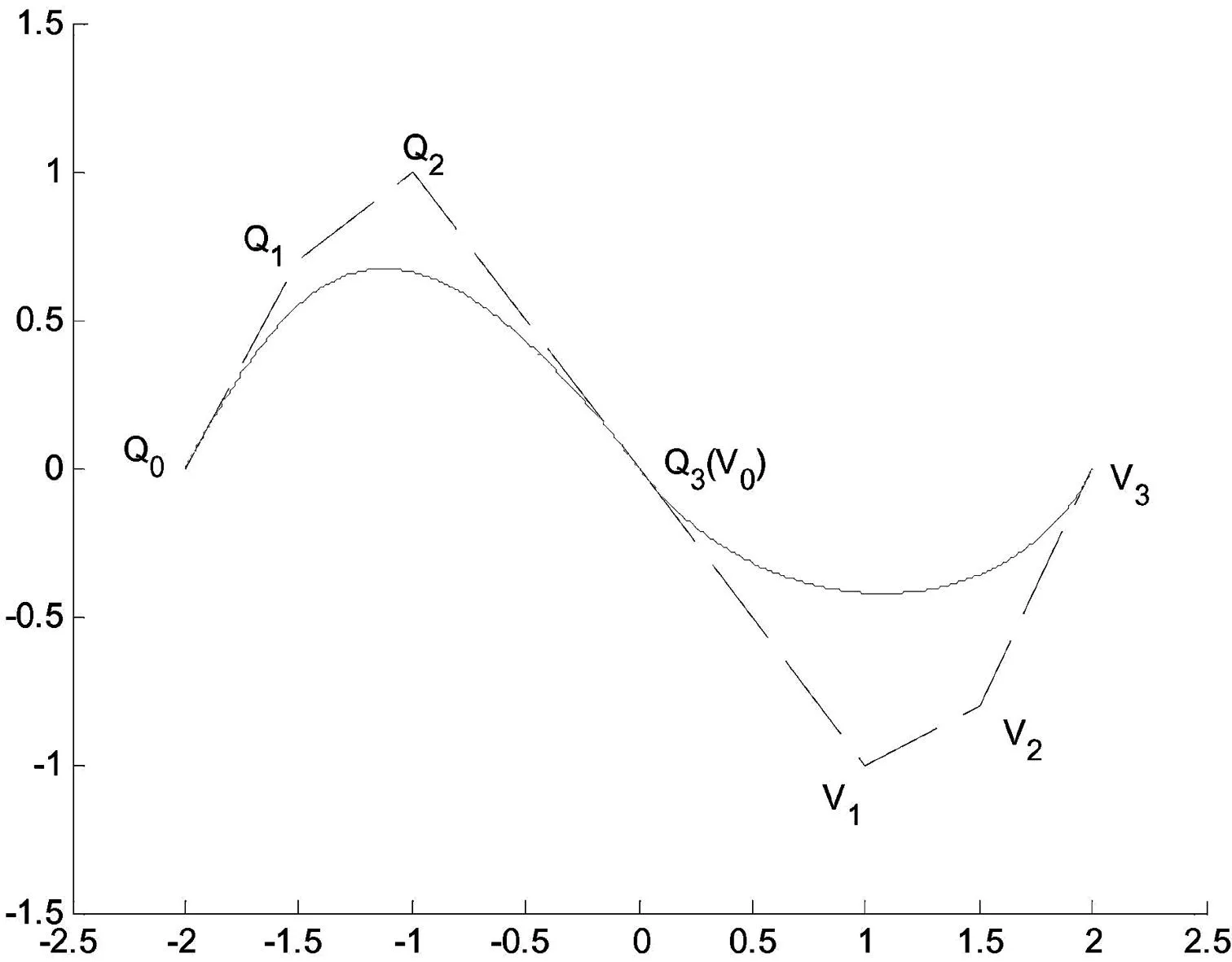
图2有理Bézier曲线与HC-Bézier曲线的光滑拼接
3.3G2光滑拼接
定理3三次有理Bézier曲线P(u)与三次HC-Bézier曲线R(t)的G2光滑拼接的充要条件是,
1)Q3=V0.
2)存在δ>0,使得,
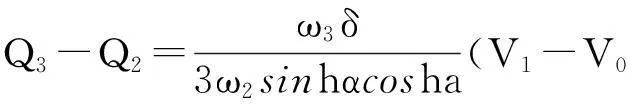
许多人都说学习中医需要悟性,成为名医需要天赋[6]。殊不知这里所谓的悟性和天赋是在扎实的基本功基础之上才能获得的,是在对《内经》深刻感受的基础上,获得某种灵感,这种领悟能力能使人更容易接近事物,更容易在人的思维活动中形成跳跃式的拓展,产生新颖的想法。正如《素问·八正神明论》中所言“目明心开而志先,慧然独悟,口弗能言,俱视独见,适若昏,昭然独明,若风吹云,故曰神。”《内经》教学最终应该实现让学生通过广博深厚的经典知识积累,并立足临床实践,对临床中的有关问题锲而不舍地追究深思,塑造真正具有中医思维的中医人。
3)存在h1、h2,使得,
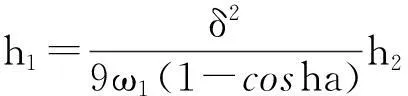
式中,h1为点Q1到边Q2Q3的距离,h2为点V2到边V0V1的距离.
证明三次有理Bézier曲线P(u)与三次HC-Bézier曲线R(t)的G2光滑拼接, 条件1)、2)已由定理1、定理2证明.
此外,2条不同的曲线首末端点的一阶导矢与二阶导矢应满足如下关系式,
化简得,
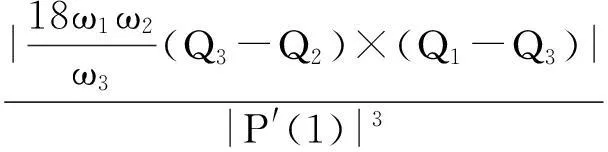
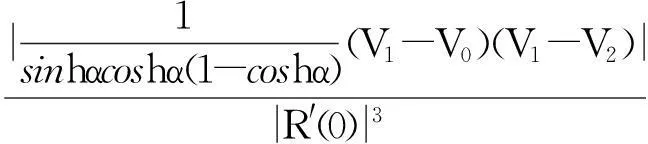
由定理2知,
P′(1)=δR′(0),
则,
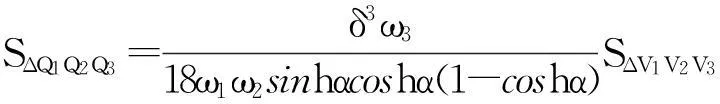
又因为,
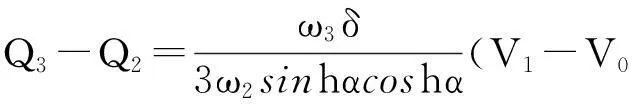
于是有,
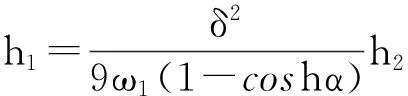
其中,h1为点Q1到边Q2Q3的距离,h2为点V1到边V0V1的距离.
则两曲线P(u)与R(t)在公共连接点处G2光滑拼接,见图3.
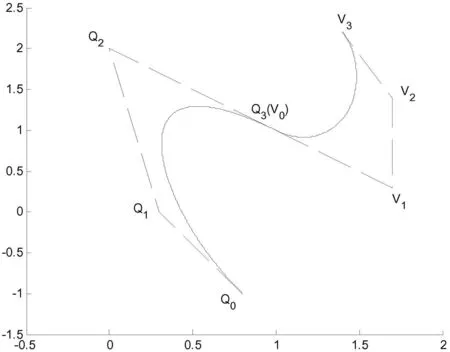
图3有理Bézier曲线与HC-Bézier曲线的G2光滑拼接
4结语
Bézier曲线在计算机辅助几何设计中有着广泛的应用,本研究讨论了三次有理Bézier曲线与带一个形状参数的HC-Bézier曲线的光滑拼接问题,并给出了三次有理Bézier曲线与HC-Bézier曲线的G0、G1和G2光滑拼接的几何条件.该方法对曲线设计人员有一定的帮助,也可促进对带形状参数的其他类型Bézier曲线拼接问题的进一步探讨.
参考文献:
[1]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京:高等教育出版社,2001.
[2]胡钢,张念娟,秦新强,等.带多形状参数的三次Bézier曲线曲面的光滑拼接[J].西安理工大学学报,2009,25(4):482-486.
[3]杨林英,张贵仓.λαβ-Bézier曲线与三次Bézier曲线的拼接条件[J].江西师范大学学报(自然科学版),2011,55(11):621-623.
[4]孙洁保,江平,程彪,等.TC-Bézier曲线曲面拼接[J].山东理工大学学报,2011,25(3):39-43.
[5]苏本跃,盛敏.基于双曲函数的Bézier型曲线曲面[J].计算机工程与设计,2006,27(3):370-372.
Research on Smooth Connections Between Cubic Rational Bézier Curves and HC-Bézier Curves
ZHANGDandan,WUHuanhuan
(Anqing Campus, Anhui Open University, Anqing 246001, China)
Abstract:Research has been done on Bézier curves and surfaces with shape parameters and the smooth connections between them in computer aided geometric design (CAGD).This paper studies the technique of smooth connections between cubic rational Bézier curves and cubic HC-Bézier curves with a shape parameter and finally puts forward the geometrical conditions for the smooth connections between the cubic rational Bézier curves and cubic HC-Bézier.
Key words:rational Bézier curve;HC-Bézier curve;shape parameter;continuity condition
中图分类号:TP391.72
文献标志码:A
作者简介:张丹丹(1984 — ), 女, 硕士, 讲师, 从事计算机辅助几何设计研究.
收稿日期:2016-01-15.
文章编号:1004-5422(2016)01-0041-03
