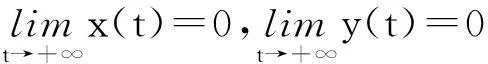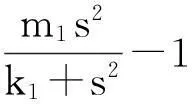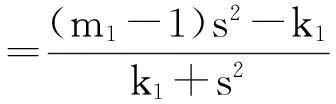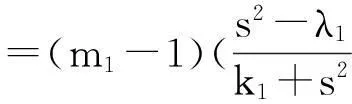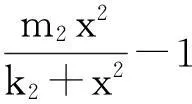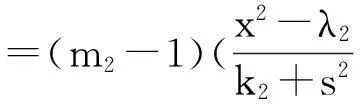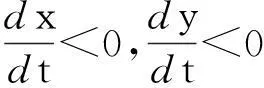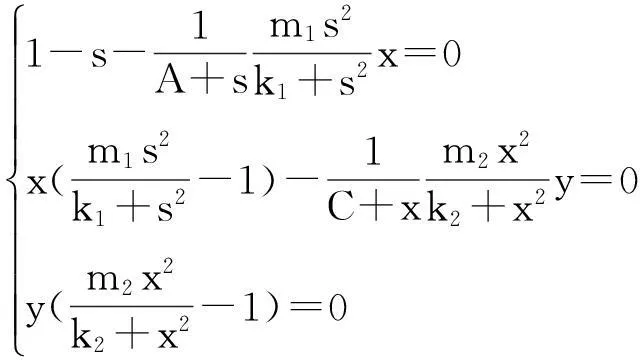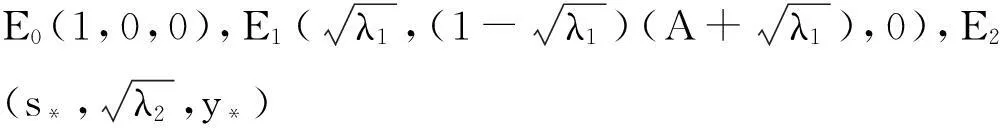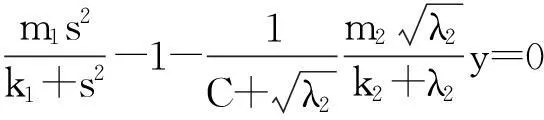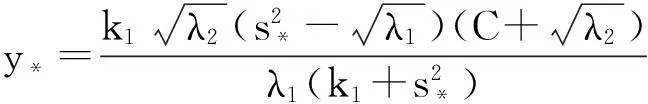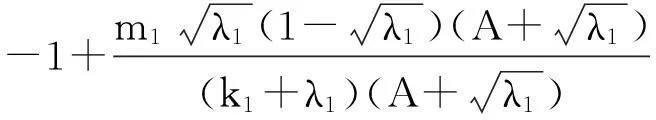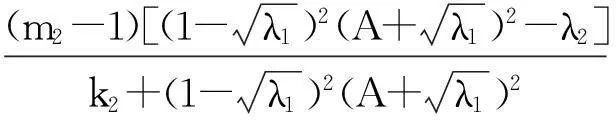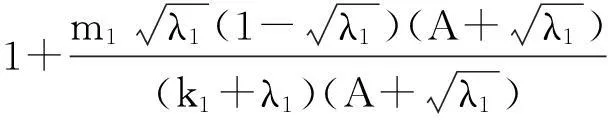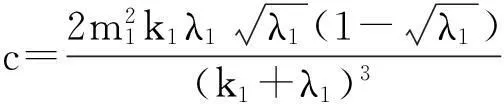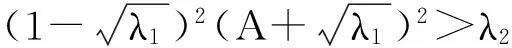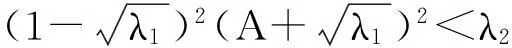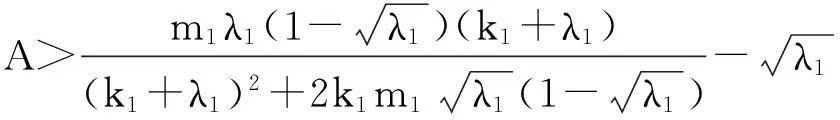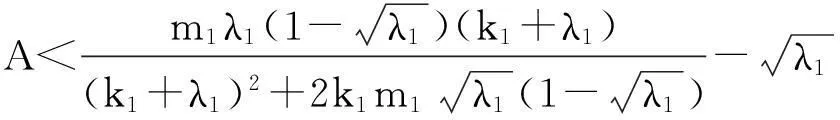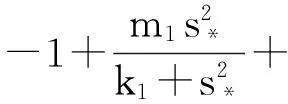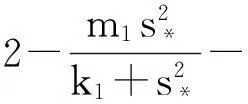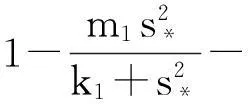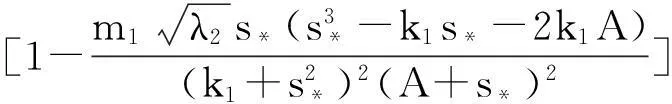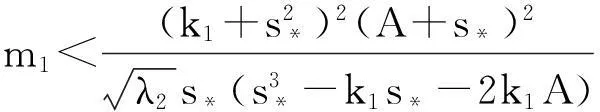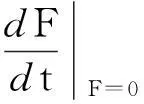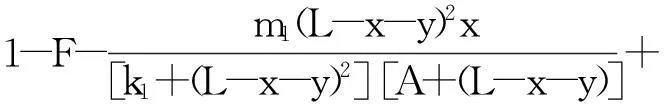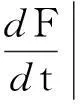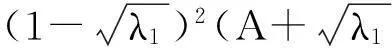具有非常数消耗率的单营养食物链2种群微生物模型定性分析

王永丽

(江苏财会职业学院 基础部， 江苏 连云港　222061)



具有非常数消耗率的单营养食物链2种群微生物模型定性分析

王永丽

(江苏财会职业学院 基础部， 江苏 连云港222061)

摘要：假设被捕食者种群对营养基的增长率为μ1(s)=m1s2/(k1+s2)，捕食者种群对被捕食者种群的增长率为μ2(x)=m2x2/(k2+x2)，被捕食种群对营养基的消耗率参数为δ1=A+Bs，捕食种群对被捕食种群的消耗率参数为δ2=C+Dx.利用常微分方程的定性理论,分析了系统平衡点的稳定性，证明了系统存在正向不变集，得到非常数消耗率单食物链模型中2种微生物共存与微生物本身的参数及环境参数之间的关系.

关键词：微生物；食物链培养；恒化器；平衡点的稳定性；不变集

0引言

恒化器(Chemostat)是人工用于连续培养微生物的实验装置.Chemostat系统可以用来研究微生物种群在营养限制条件下的生长，其模型的研究对微生物的生产和污水处理等都有很重要的作用.目前，科研人员对Chemostat模型的研究已取得一定成果[1-8]，例如，庞国萍等[3]讨论了单种微生物培养和单营养食物链2种微生物培养的全局稳定性，刘婧等[4]对消耗率参数一次函数的单食物链模型进行了定性研究，凌志超等[5]讨论了三维单食物链种群竞争模型系统解的稳定性．在此基础上，本研究主要考虑三维单食物链种群模型.假设：δ1=A+Bs,δ2=C+Dx，被捕食者种群对营养基的增长率μ1(s)=m1s2/(k1+s2)，捕食者种群对被捕食者种群的增长率为μ2(x)=m2x2/(k2+x2)，并对系统进行了定性分析.

1模型建立

单营养食物链的2种微生物培养是将有捕食与被捕食关系的2种微生物x、y混合在一个培养室，其中微生物x以营养基S作为营养物，x培养繁殖后，y又以x作为营养物.而微生物y和营养基S没有直接的关系，S不直接作为y的营养物.其相应的模型系统为，

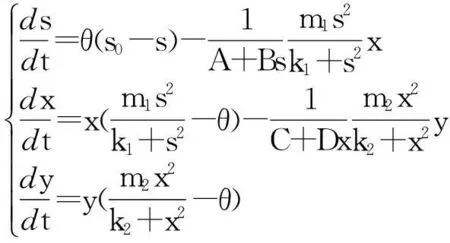
(1)

系统的初始条件为：s(0)=s0≥0,x(0)=x0≥0,y(0)=y0≥0，其中：s,x,y分别代表营养基和第1、2种微生物在t时刻的浓度；参数θ表示营养输入输出量；s0为供液源流中营养基的浓度；δ1=A+Bs,δ2=C+Dx分别代表捕食者微生物x,y对被捕食者s,x的消耗率.ki>0,mi>0(i=1,2)分别代表2种微生物x,y的半饱和常数和最大增长率.A、B、C、D均为正常数.

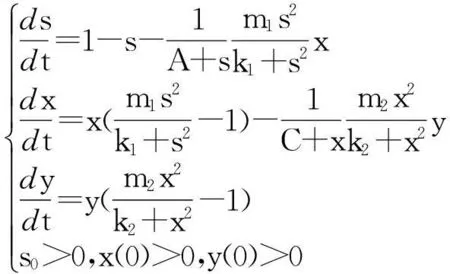
(2)

系统(1)中，s(t)总不会比初始流入的供液中营养基的浓度s0大，因此系统(2)中，必有0

证明系统(2)的第2个方程中，

系统(2)的第3个方程中，

定理1表明，当微生物种群本身的参数最大增长率mi≤1(较小)或mi>1(较大)但半饱和常数ki≥(mi-1)也较大时，微生物种群不能存活.因此，为了使研究有意义，对微生物本身的参数做如下假设，mi>1且λi<1.

考虑系统(2)的平衡解，解方程组，

(3)

(4)

令，

(5)

系统(2)的线性化矩阵为，

证明系统(2)在E0处的线性化矩阵为，

系统(2)在E1处的线性化矩阵为，

在E1处的特征方程为，

设其根为，r1,r2,r3，其中,

特征根为，

系统(2)在E2处的线性化矩阵为，

在E2处的特征方程为，

r3+b1r2+b2r+b3=0

其中，

b1>0，b1b2-b3>0

(6)

时，由霍维茨判别法知，E2是稳定的平衡点.

2结论

参考文献：

[1]王文娟，冯晓梅，龚固斌.单种群时滞反馈控制生态系统的全局稳定性[J].中南林业科技大学学报，2011,31(4)：210-213.

[2]阎恩让，王爱丽.具有三个成长阶段的多种群捕食模型的全局稳定性[J].福州大学学报(自然科学版)，2014,42(4)：514-518.

[3]庞国萍，陈兰荪.比例确定增长率Chemostat模型的全局稳定性[J]．广西师范大学学报(自然科学版)，2006,24(1)：37-40.

[4]刘婧,杨淑芹.恒化器中微生物连续培养单食物链模型的定性分析[J].大连海事大学学报，2004,30(3)：88-91.

[5]凌志超，张天四.恒化器中一类具有非常数消耗率微生物培养模型的定性分析[J].上海理工大学学报，2012,34(4)：373-376.

[6]王晖，李冬梅，郭秀微.一类具有时滞的Lotka-Volterra捕食系统的持久性与全局稳定性[J].哈尔滨理工大学学报，2009,14(6)：73-76.

[7]Li H Y,Zhang R.Stabilityandoptimalharvestingofadelayedratio-dependentPredator-preysystemwithstagestructure[J].J Biomath，2008,23(1)：40-52.

[8]刘三红.一类具有时滞的恒化器模型的定性分析[J].佳木斯大学学报(自然科学版)，2012,30(2)：295-296.

Qualitative Analysis of Two Species Microbial Models with Non-constant Consumption Rate in Single-nutrition Food Chain

WANGYongli

(Department of Fundermentals, Jiangsu College of Finance and Accounting, Lianyungang 222061, China)

Abstract:It's assumed that the growth rate of the nutrition basis for the prey species is μ1(s)=m1s2/(k1+s2)，the growth rate for the prey species with respect to the predator species is μ2(x)=m2x2/(k2+x2),the consumption rate of the nutrition basis for the prey species is δ1=A+Bs，the consumption rate for the prey species with respect to the predator species is δ2=C+Dx.The paper analyzes the stability of equilibrium point by the qualitative theory of the ordinary differential equation,and proves that there exists a positive invariant set and finds the relationship between the coexistence of two microorganisms and the parameters of the microorganisms themselves as well as the environmental parameters in a single food chain model with a non-constant consumption rate.

Key words:microorganism;cultivation of food chain;chemostat;stability of equilibrium point;invariant set

中图分类号：O175；Q141

文献标志码：A

作者简介：王永丽(1982 — )， 女， 硕士， 讲师， 从事生物数学研究.

收稿日期：2015-12-22.

文章编号：1004-5422(2016)01-0044-05