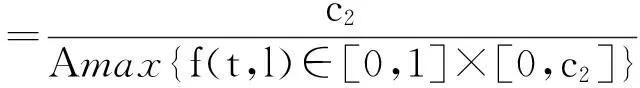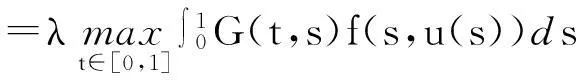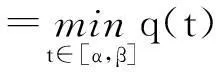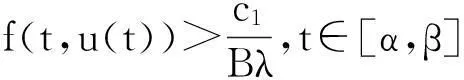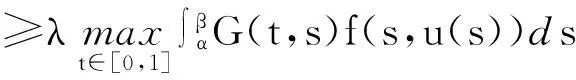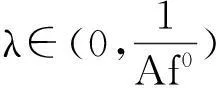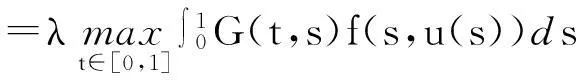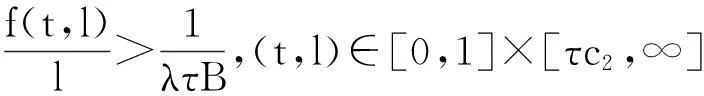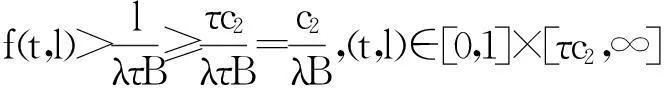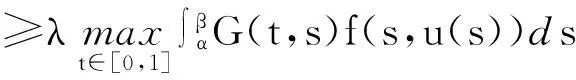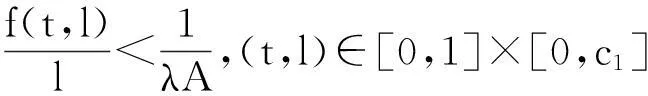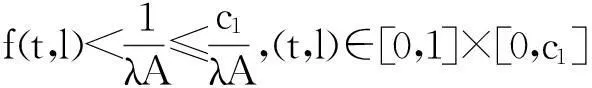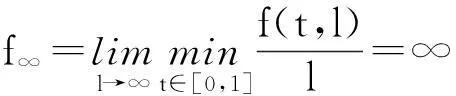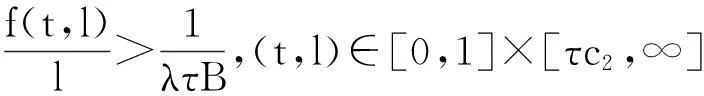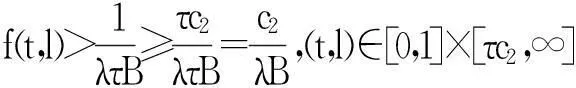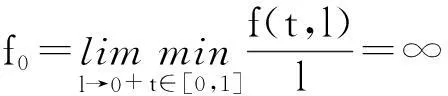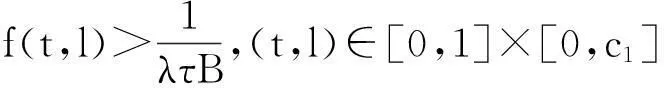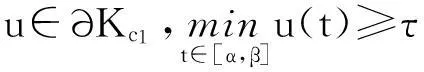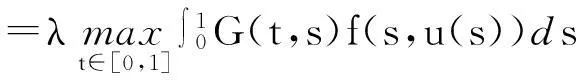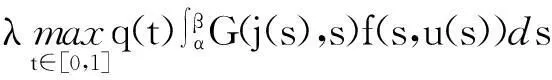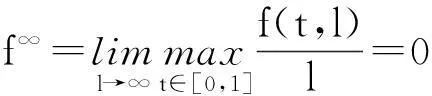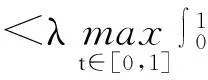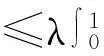一类四阶两点边值问题正解的存在性

鞠梦兰, 王文霞, 郝彩云

(太原师范学院 数学系, 山西 晋中　030619)



一类四阶两点边值问题正解的存在性

鞠梦兰, 王文霞, 郝彩云

(太原师范学院 数学系, 山西 晋中030619)

摘要：应用锥上的不动点指数理论，研究了一类四阶两点边值问题正确的存在性，给出该问题至少有一个正解的充分条件，即该方程的解对参数的依赖性结果.

关键词：四阶边值问题；正解；锥；不动点指数

0引言

考虑如下四阶边值问题，

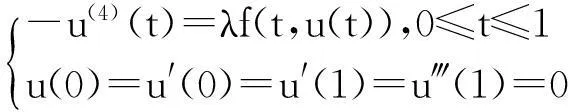
(1)

正解(1)的存在性，其中f:[0,1]×[0,+∞)→[0,+∞)连续，λ>0.

目前，对于两端固定的梁的研究大多数是在边界条件为，

u(0)=u(1)=u′(0)=u′(1)=0

(2)

的情况下进行分析，科研人员对这类方程的研究已取得了许多成果[1-4].但对于一端固定且一端滑动支撑的梁,即问题(1)，目前的相关报道较少.对此，陆海霞等[5]给出了在未加参数时通过不动点指数方法,在与相应线性算子第一特征值有关的条件下得到了其至少有一个正解的结果.在此基础上，本研究通过讨论问题(1)的Green函数的性质,结合锥理论以及锥上的不动点指数定理,给出问题(1)的正解的存在性结果,并对文献[5]中相关的结论做了推广.

1预备和记号

引理1设，

则，G(t,s)是边值问题，

的格林函数.

为了讨论G(t,s)的性质，定义j(s):[0,1]→[0,1]，如下，

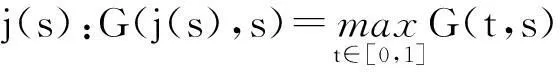
(3)

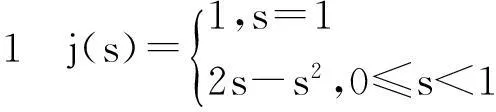
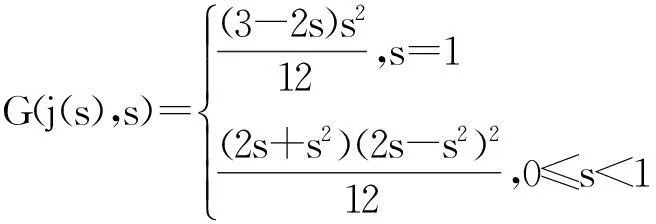
命题2对∀t,s∈[0,1]，j(s)如上所记，则G(t,s)有以下性质：

1)G(t,s)≥0，G(t,s)≤G(j(s),s)，

证明1)依照G(t,s)及j(s)的定义可知，性质1)显然成立.

2)分以下4种情况：

①当0≤t≤j(s)≤s≤1，

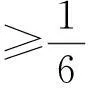
②当0≤t≤s≤j(s)≤1，

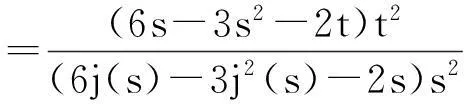
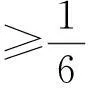
③当0≤j(s)≤t≤s≤1，

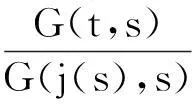
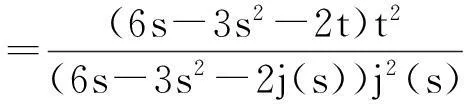
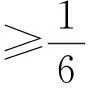
④当0≤s≤t≤j(s)≤1，

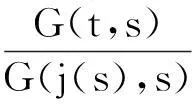
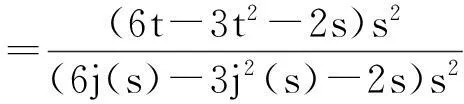
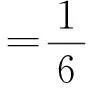
原命题得证.

下面给出一些记号：

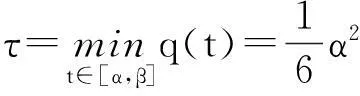
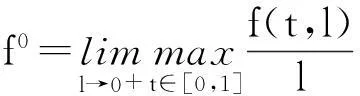
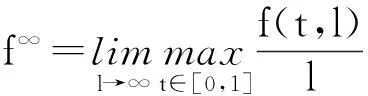
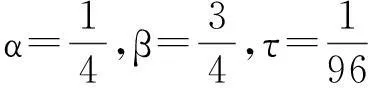
且，

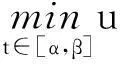
(4)

则K为C[0,1]中的锥，记，∂Kc={u∈K：‖u‖=c}

定义算子Tλ:C[0,1]→C[0,1]为，

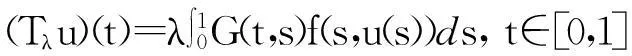
(5)

则，若u*是BVP(1)的解等价于u*是Tλ的不动点.

引理2Tλ是K→K全连续算子.

证明设u∈K，由G(t,s)≥0,(t,s)∈[0,1]×[0,1]，且由Tλ的定义知，

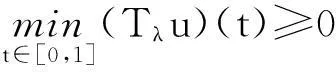
另外，

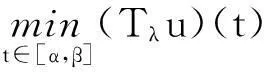
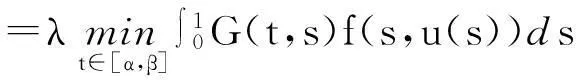
=τ‖Tλu‖

再由Arzera-Ascoli定理，即原命题得证.

引理3[6]设X是一Banach空间，K⊂X是X中的一个锥，对任意的p>0，令，Kp={x∈K:‖x‖

1)‖x‖<‖Fx‖,x∈∂Kp，蕴含i(F,Kp,K)=0；

2)‖x‖>‖Fx‖,x∈∂Kp，蕴含i(F,Kp,K)=1.

2主要结果

定理1若存在c1，c2>0，且c1≠c2,使得，

=a

(6)

成立，则当λ∈(a,b)时，BVP(1)至少有一个正解u*，

0

(7)

证明BVP(1)的有解性等价于Tλ的不动点，不妨设c2>c1，则，

一方面，若u∈∂Kc2，则，

0≤u(t)≤‖u‖=c2,t∈[0,1]

=c2

=‖u‖

所以，

i(Tλ，Kc2，K)=1

(8)

另一方面，若u∈∂Kc1，

同理由式(6)可知，

从而有，

=c1=‖u‖

所以，

i(Tλ,Kc1，K)=0

(9)

综合式(8)、(9)有，

i(Tλ，Kc2/Kc1，K)

=i(Tλ，Kc2，K)-i(Tλ，Kc1，K)=1

(10)

则，Tλ有一个不动点u*，且，0

f(t,l)<(f0+ε)l,(t,l)∈[0,1]×[0,c1]

取u∈K,且‖u‖=c1，即，u∈∂Kc1，有，

=λA(f0+ε)‖u‖

≤‖u‖

所以，

i(Tλ,Kc1，K)=1

(11)

则有，

若u∈∂Kc2，有，

=c2=‖u‖

所以，

i(Tλ，Kc2,K)=0

(12)

综合式(11)、(12)有，

i(Tλ，Kc2/Kc1，K)

=i(Tλ,Kc2，K)-i(Tλ,Kc1，K)=-1

(13)

则，Tλ至少有一个不动点u*.证毕.

定理3若下列条件之一成立：

1)f0=0,f∞=∞;

2)f0=∞,f∞=0.

则对任意λ∈(0,∞),BVP(1)至少有一个正解.

则有，

(14)

则有，

(15)

综合式(14)、(15)，同定理1证明方法一致，则，Tλ有一个不动点u*.

所以，

i(Tλ，Kc1，K)=0

(16)

1)若f是有界的.设f

=λAM≤c0=‖u‖

即，‖Tλu‖≤‖u‖，记，Kc0={u∈K:‖u‖

i(Tλ,Kc0，K)=1

(17)

2)若f是无界的.c0>max{2c1,c2}，使得，

f(t,l)

对u∈K,‖u‖=c0，则，

=c0=‖u‖

即，‖Tλu‖≤‖u‖,记，Kc0={u∈K:‖u‖

i(Tλ,Kc0，K)=1

(18)

综合式(16)～(18)，可知无论在哪种情况下都有，

i(Tλ,Kc0/Kc1，K)

=i(Tλ,Kc0，K)-i(Tλ,Kc1，K)=1

(19)

则，Tλ有一个不动点u*.

参考文献:

[1]马如云,吴红萍.一类四阶两点边值问题多个正解的存在性[J].数学物理学报,2002,22A(2):244-249.

[2]吴红萍,马如云.一类四阶两点边值问题正解的存在性[J].应用泛函分析学报,2000,2(4):342-348.

[3]Yao Q.Positivesolutionsforeigenvalueproblemsoffourth-orderelasticbeamequations[J].Appl Math Lett,2004,17(2):237-243.

[4]闫东明.一类四阶两点边值问题多个正解的存在性[J].工程数学学报,2010，27(1)：133-138.

[5]陆海霞,孙经先.一类四阶非线性微分方程两点边值问题的正解[J].数学的实践与认识,2014，45(8)：229-235.

[6]Erbe H,Hu S C,Wang H Y.Multiplepositivesolutionsofsomeboundaryvalueproblems[J].J Math Anal Appl，1994,184(3)：640-648.

Existence of Positive Solution to Fourth-order Two-point Boundary Value Problem

JUMenglan,WANGWenxia,HAOCaiyun

(Department of Mathematics, Taiyuan Normal University, Jinzhong 030619, China)

Abstract:By using the fixed point index theory,the paper studies the existence of positive solution to the fourth-order boundary value problem and puts forward the optimal sufficient conditions for the existence of at least one positive solution to the problem mentioned above,namely,the result of the dependence of the solution to the parameter.

Key words:fourth-order boundary value problem;positive solution;cone;fixed point index

中图分类号：O177.91；O175.8

文献标志码：A

作者简介：鞠梦兰(1991 — )， 女， 硕士研究生， 从事非线性算子研究.

基金项目：国家自然科学基金(11361407)资助项目.

收稿日期：2016-01-25.

文章编号：1004-5422(2016)01-0037-04