求解悬臂梁受迫振动的时域DQ法

林　凡, 彭建设, 杨　柳, 刘　雄

(1.西华大学 机械工程学院， 四川 成都　610039； 2.成都大学 机械工程学院， 四川 成都　610106)



求解悬臂梁受迫振动的时域DQ法

林凡1, 彭建设2, 杨柳2, 刘雄1

(1.西华大学 机械工程学院， 四川 成都610039； 2.成都大学 机械工程学院， 四川 成都610106)

摘要：针对悬臂梁分别施加突加荷载F(x,t)=Q与交变荷载F(x,t)=Q·sinωt时的定解问题，提出对控制微分方程及定解条件直接进行离散求解的时域DQ法.该方法在空间域和时间域均采用离散的DQ法，得到全部离散点挠度的可解线性方程组，求解该线性方程组即可得到全域位移场.算例分析结果表明，时域DQ法比有限元法速度快且精度高.

关键词：悬臂梁；定解问题；时域DQ法；受迫振动

0引言

传统的对梁振动问题的数值计算一般都采用在空间域做有限元离散，且在时间域差分的方法.这种方法需把所经历的时间域分成递推求解，每一步递推都要对所给定的空间域解一次稳定问题.为了解的稳定性和精度，时间步长往往必须取得很短，网络也必须划得较细，这样使得求解较为繁琐，大大影响了计算效率.

DQ法(Differential Quadrature Method)是Bellman等[1]于1969年提出的一种求解偏微分方程的数值解法.该算法数学推理简单，计算过程易于编程，计算成本低，计算精度高，在相关领域得到了较广泛的应用[2-3].

本研究针对2种不同策动力作用下悬臂梁的受迫振动响应问题，直接从控制微分方程出发提出了求解策动力下动力学定解问题的时域DQ法.该方法对控制方程及其边界条件在空间域和时间域都应用DQ法，得到全域内离散点挠度的线性方程组，通过求解方程组，便能得到全域内的梁振动位移响应场.

1时域DQ法求解控制方程

受迫振动悬臂梁的控制微分方程为，

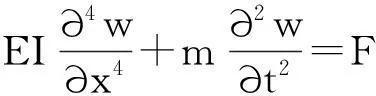
(1)

式中，w为悬臂梁小挠度，x为轴向自变量，t为时间自变量，E为弹性模量，I为横截面转动惯量，m为单位长度质量，F为梁横向荷载.

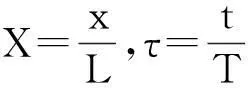
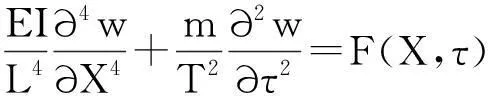
(2)

式中，L为悬臂梁的长度，T为时间域长.

在梁的空间域内取NX个节点，时间域内取Nτ个节点，即全域内有NX×Nτ个节点.由DQ法的基本原理[4]知，挠度w对空间X和时间τ的各高阶偏导数在无量纲坐标(Xi,τj)处的函数值可以用全域内各节点值的加权和表示，即任意节点(Xi,τj)处的n(自然数)阶偏导数可表示为，

(3)

(4)

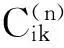
由式(3)、(4)代入式(2)得全域内关于控制方程的时域DQ线性方程组，

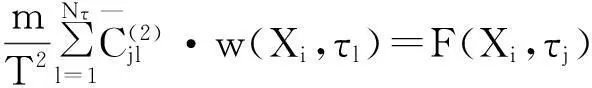
(5)

式中，i=1,2,…，NX；j=1,2,…，Nτ.

易知，在全域内有NX×Nτ个关于控制方程的时域DQ线性方程组，式(5)的矩阵形式为，

[C]·{w}={F}

(6)

式中，{w}为全域内节点(Xi,τj)处梁挠度w(Xi,τj)组成的NX×Nτ行、1列矩阵，[C]为NX×Nτ行、NX×Nτ列的权系数矩阵，{F}为NX×Nτ行、1列的广义荷载列阵.

为求解时域DQ线性方程组式(5)，还需确定其定解条件.对悬臂梁，利用在任意时间节点τj(j=1,2,,…，Nτ)处，梁的两端点都有4个边界条件方程，则全域内共有4Nτ个边界条件方程.

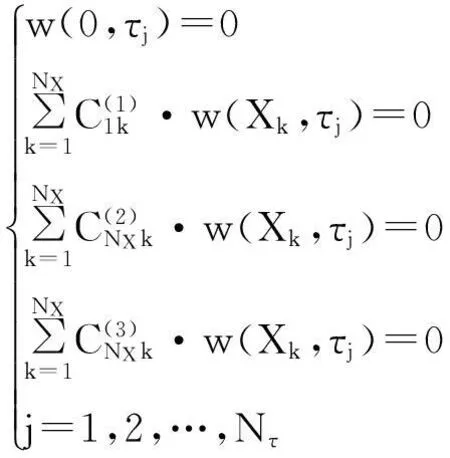
(7)

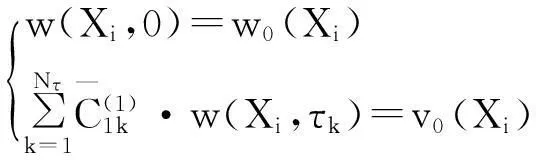
(8)

式中，i=1,2,…，NX.

用式(7)的4Nτ个边界条件时域DQ法方程和式(8)的2NX个初始条件时域DQ法方程，分别代替式(5)中的i=1,2,NX-1,NX(j=1,2,…，Nτ)，j=1,2(i=1,2,…，NX)时表示的时域DQ法方程，将定解条件融入到可解线性方程组式(5)，即得到式(6)的系数矩阵[C]和荷载列{F}，从而求解式(6)可得到全域内已知节点处的挠度列阵{w}.于是，全域内的位移场可由Lagrange插值得到，

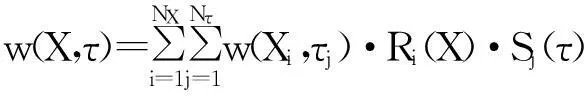
(9)

至此，全域内的时程响应已经得到.

在此基础上，根据DQ法可以进一步求得已知各节点处的速度和加速度，即，

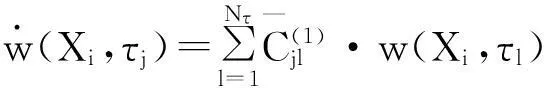
(10)

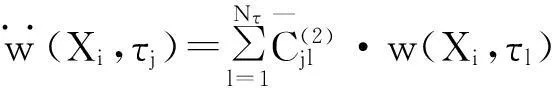
(11)

利用求出的{w}以及式(10)和式(11),采用高阶Lagrange插值,可以得到全域内的速度和加速度分别为，

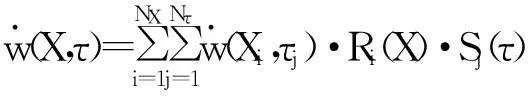
(12)

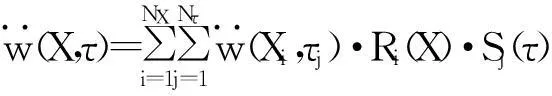
(13)

同理，由薄板在全域内的应力场表达式[7]，

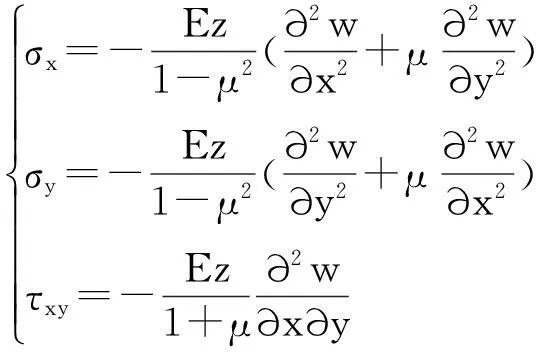
(14)

得到悬臂梁在全域内的应力场表达式为，

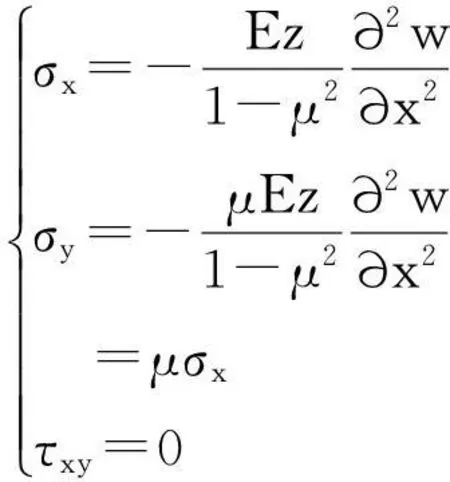
(15)

式中，μ为泊松比，z为悬臂梁挠度方向自变量，设为已知量.

根据式(9)，可求得已知节点(Xi,τj)处的应力为，

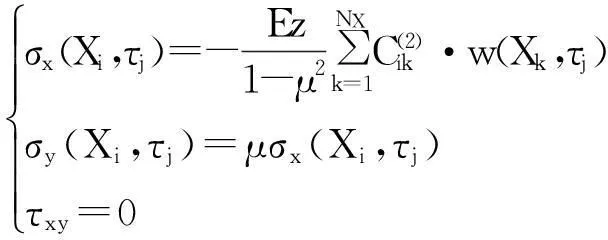
(16)

再采用高阶Lagrange插值,可得全域内的应力场表达式，

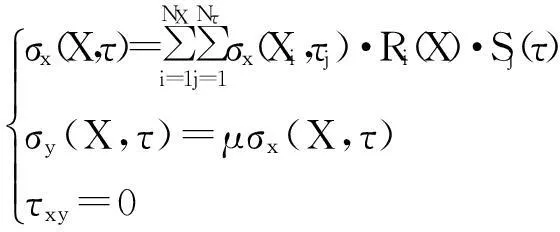
(17)

对式(9)、(12)中τ=1时的值，可作为下一时域段的初始条件，再按照前述方法,可求得下一时域段的动力响应和应力场.如此往复,即可求得任意时刻悬臂梁振动的时程响应和应力场.

2算例分析与讨论

2.1算例分析

例1左端固定右端自由悬臂梁，长50cm，截面高2cm，宽1cm，弹性模量E=15 000 000N/cm2，质量密度ρ=0.008kg/cm3.初始位移和初始速度均为0，在梁上作用突加荷载F(x,t)=10N/cm，求自由端的位移响应.

例2同例1几何物理参数相同的悬臂梁,在梁上作用交变荷载F(x,t)=10sin500tN/cm，求自由端的位移响应.

对上述2个算例，本研究分别采用时域DQ法和有限元法进行求解，其中，有限元(Ansys 14.0)单元类型为solid185.2种算法的时间域区间长度都取0.3 s，全域内具体节点数的选取如表1所示.图1和图2为采用以上2种算法求解算例的数值解与精确解的位移响应汇总图.

表1　2种数值解法在全域内的节点数

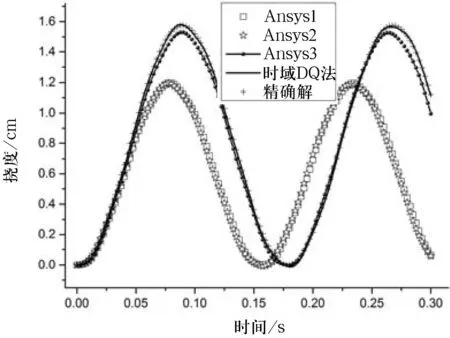
图1算例1的时间——位移响应

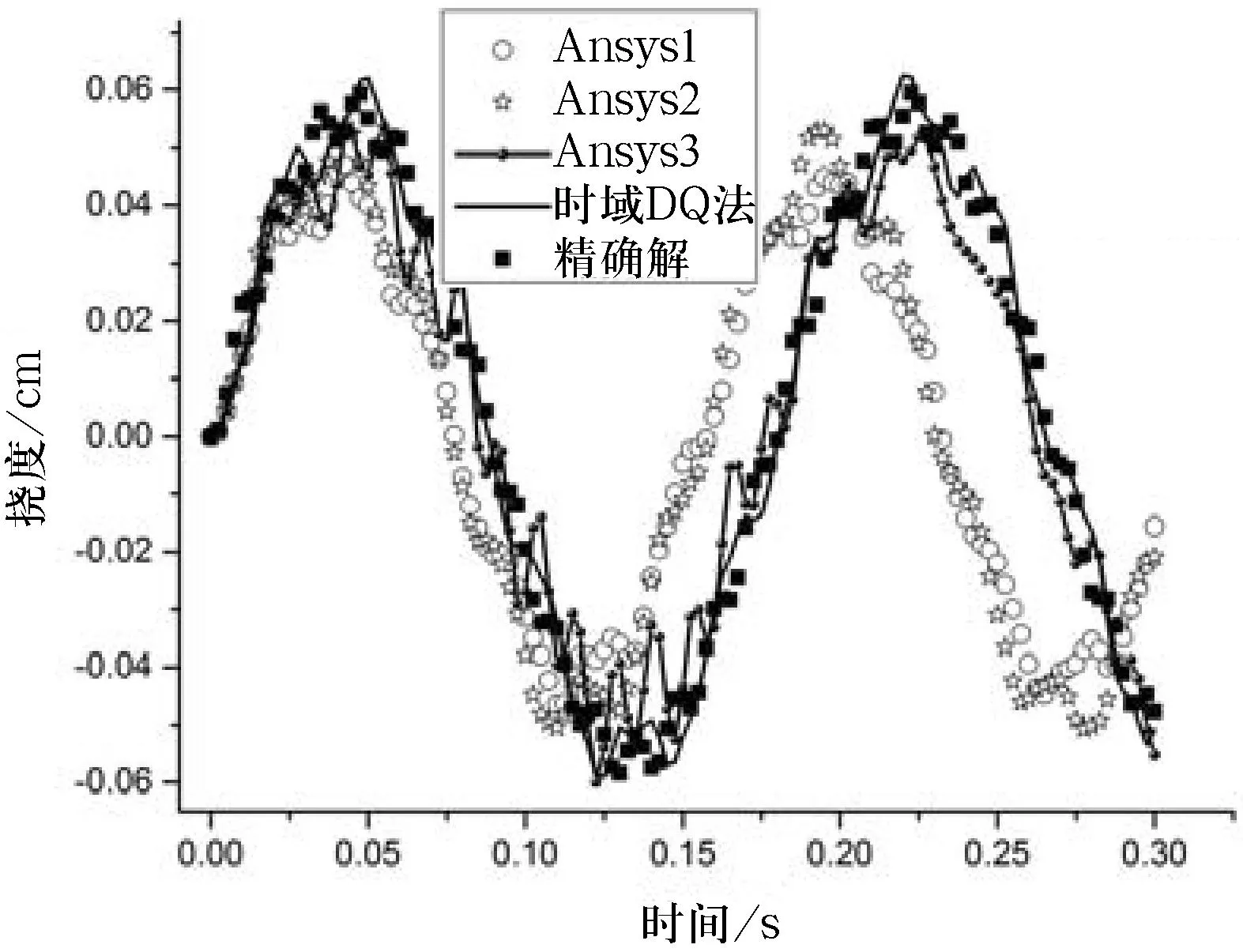
图2算例2的时间——位移响应

需说明的是，时域DQ法是一维数学模型，空间域取梁长方向；有限元(Ansys14.0)是三维数学模型，空间域为长×宽×高，所以2种方法在比较空间域节点数时只讨论梁长方向.

2.2讨论

对于算例1，从表1和图1可知，在空间域(指梁长方向，下同)节点数都为31，时间域节点数都为120时，时域DQ法的精度明显比Ansys1好很多；仅当有限元的时间域节点数增加到4倍于Ansys1时，Ansys2的精度较Ansys1几乎没有改善；仅当有限元的空间域节点数增加到3倍于Ansys1时，Ansys3的精度与时域DQ一样有很好的精度.同样，从表1和图2，算例2也可得出与算例1相同的结论.

3结语

从本研究的分析与计算过程看，时域DQ法原理简单，且易于编程实现计算.因此，在求解动力学问题方面，时域DQ法计算精度和计算效率都大大优于有限元法.

参考文献：

[1]Bellman R，Casti J.Differentialquadratureandlong-termintegration[J].J Math Anal Appl，1969,34(2)：235-238.

[2]Bert C W,Malik M.Differentialquadraturemethodincomputationalmechanics:areview[J].Appl Mech Rev,1995,49(1):1-27.

[3]Chen W,Zhong T.Differentialquadraturemethodanditsapplicationsinengineering[D].Shanghai:Shanghai Jiaotong University,1996.

[4]Peng Jianshe，Zhang Ying，Yang Jie.DQspace-timesemi-analyticmethodofdynamicsinitial-boundaryvalueproblemsunderalternateforce[J].Chin J Comput Phys，2000，17(2):54-58.

[5]张晓丹.应用计算方法教程[M].北京：机械工业出版社，2008.

[6]徐次达，陈学潮，郑瑞芳，等.新计算力学加权残值法——原理、方法及应用[M].上海：同济大学出版社，1997.

[7]徐芝纶.弹性力学(下)[M].北京：高等教育出版社，2006.

Forced Vibration of Cantilever Beams by Time-domain Differential Quadrature

LINFan1,PENGJianshe2,YANGLiu2,LIUXiong1

(1.School of Mechanical Engineering, Xihua University, Chengdu 610039, China;2.School of Mechanical Engineering, Chengdu University, Chengdu 610106, China)

Abstract:Aiming at the definite solution problems for suddenly applied load and alternative load put on cantilever beams,a time-domain DQ(differential quadrature) method is presented in this paper which directly makes discrete solution to governing partial differential equation and definite condition.This method adopts discrete DQ both in space domain and time domain and obtains the system of linear equations of all the discrete point deflection.Solving this system of linear equations can obtain the whole domain displacement-field.The numerical examples show that the computational accuracy and efficiency of time-domain DQ method are better than that of finite element method.

Key words:cantilever beam;definite solution problems;time-domain DQ method;forced vibration

中图分类号：O302；O175.2

文献标志码：A

作者简介：林凡(1989 — )， 男， 硕士研究生， 从事计算固体力学研究.

收稿日期：2016-01-25.

文章编号：1004-5422(2016)01-0034-04