基于多辐射源目标测角的平台自定位与测姿技术

石　荣，姜道安，李　潇

(电子信息控制重点实验室，成都　610036)

石　荣(1974—)男，四川人，博士，研究员，主要研究方向为电子对抗，导航定位，通信与雷达系统等；

E-mail：wyx1719@sina.com

姜道安(1965—)男，江苏人，研究员，主要研究方向为电子对抗；

李　潇(1993—)女，甘肃人，硕士研究生，主要研究方向为电子对抗。



工程与应用

基于多辐射源目标测角的平台自定位与测姿技术

石荣，姜道安，李潇

(电子信息控制重点实验室，成都610036)

摘要：基于辐射源目标地图的导航具有天然的隐蔽性、顽存性和抗外界干扰的能力，成为战场高对抗条件下多样化导航的一种重要方式。针对这一应用中的单平台导航问题，建立了平台自定位与姿态测量的数学模型，利用多棱锥体在不同坐标系下所具有的空间几何不变性，实现了平台位置参数与姿态参数的解耦和各自的独立求解，极大地降低了模型求解的复杂度。接着从空间解析几何的角度解释了基于多辐射源目标测角的平台自定位与测姿的几何物理意义，并在此基础上分析和讨论了模型的求解条件，最后通过仿真验证了模型求解的有效性，从而为该导航方式的工程实际应用提供了重要参考。

关键词：辐射源目标地图；电子侦察；测向；自定位；姿态测量；逆向无源定位；解耦；多样化导航

0引言

基于辐射源目标地图的导航是将已知位置坐标的外界辐射源作为定位参考点，利用平台上搭载的各种电子侦察设备来实施相对于上述参考点的各种物理参数的测量，并通过逆向无源定位算法求解出平台自身位置等信息的一种导航方式[1]。该导航方式中所采用的辐射源目标既可以是我方的目标，也可以是敌方或第三方的目标，既可以是军事目标，还可以是民用目标，如军用雷达，微波中继站，民用广播电台，地面电视发射台，手机基站等，都可以作为导航定位的基准参考点。相对于容易受到外界电磁干扰[2-4]和欺骗[5-7]的GPS卫星导航方式来说，基于辐射源目标地图的导航具有极强的隐蔽性和生存能力、天然的抗外界电磁干扰的能力，从而成为现代战场上顽存性导航的重要形式之一。

基于辐射源目标地图的导航主要有两种方式：单站独立导航与多站协同导航。虽然多站时差测量协同导航的精度相对较高，但是它要求站间具有数据链的实时传输与交互，使用时至少需要两个站的相互协同配合[8]，这给系统实际应用，特别是单平台导航应用带来了不便。针对这一问题，本文重点研究了单站测向交叉独立导航这一应用方式，即利用平台上的电子侦察设备对外界已知位置坐标的辐射源实施来波方向测量，通过各个测向角度参数来解算平台自身的位置和姿态信息。本文在建立了单平台自定位与测姿的数学模型之后，重点分析了该模型的求解方法与求解条件，并通过仿真对模型的有效性和正确性进行了验证。详细阐述如下。

1平台自定位与测姿的数学模型

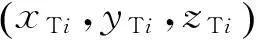
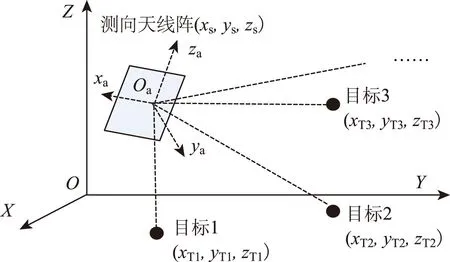
图1　平台对各个辐射源测向场景图示

(1)

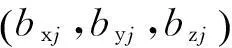
(2)

式中M1，M2，M3分别表示旋转变换矩阵，由下式所表达：

(3)

(4)

(5)

虽然在测向之后即可建立上述简洁的平台自定位与姿态测量的数学模型，但是方程组是高度非线性的，直接求解比较困难。下面将采取其它方式来获得该方程组的解。

2模型的解耦与位置参数的求解

由方程组式(1)可知：平台的位置参数与姿态参数是耦合在一起的，这主要是由于两个坐标系OaXaYaZa与OXYZ之间的姿态旋转变换式(2)所带来的。但仔细观察图1可发现，无论这两个坐标系之间的关系如何变化，平台上的Oa点与各个辐射源目标之间连线所形成的棱锥体的形状始终是保持不变的，利用这一不变性可以实现平台姿态参数与位置参数的解耦。以最少3个外辐射源目标的求解条件为例阐述如下。

在图1所示的测向场景中，平台上的Oa点、目标1，2，3之间的连线将构成一个空间四面体，如图2所示。(为了后续表述方便，将目标1，2，3所在位置处同时用字母A，B，C分别表示)。

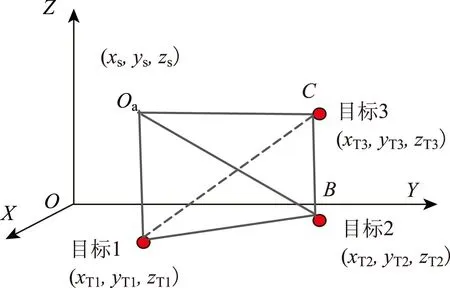
图2　由测向线与目标之间的互联线构成的空间四面体

在图2所示的四面体OaABC中，底面3条边AB，BC，AC的长度是已知的，分别记为lAB、lBC、lAC，由下式所表达：

(6)

(7)

(8)

另一方面，这3条边分别在各个侧面三角形中所对应的顶点角∠AOaB、∠BOaC、∠AOaC分别记为θ1、θ2、θ3，也是由测向线OaA、OaB、OaC所唯一决定的，如下式所表达：

(9)

(10)

(11)

由空间立体几何关系可知：利用lAB、lBC、lAC、θ1、θ2、θ3这6个已知参数可唯一确定四面体OaABC的形状大小，即可以在没有平台姿态信息的条件下直接求解出顶点Oa的位置坐标。

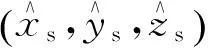
(12)

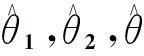
(13)

(14)

(15)

式中l1,l2,l3分别表示OaA、OaB、OaC的长度，分别由下式所表达：

(16)

(17)

(18)

将式(13)至式(18)代入式(12)，即可得到一个仅包含(xs,ys,zs)T的最优化方程，通过最陡下降法所求得目标函数最小值时的解即是平台的位置坐标。

上面是以3个辐射源目标为例进行的说明，当可利用的辐射源目标个数K>3时，每两个辐射源之间就可以与顶点Oa构成一个三角形，在该三角形中底边长度是已知的，该边所对应的顶点角度大小也是由测向线所唯一决定的，所以仍然可以按照前面的最优化求解方法进行求解，仅是式(12)中对应的角度差平方求和的项数增加了而已。

3姿态参数求解

(19)

式中lj表示平台与第j个辐射源之间的距离，即：

(20)

于是由式(2)可以建立如下的最优化方程：

(21)

式中‖•‖表示向量的长度。将式(3)至式(5)代入式(21)，即可得到一个仅包含(φ1,φ2,φ3)T的最优化方程，通过最陡下降法可求得目标函数最小值时的解即是平台的姿态参数。

4几何物理意义分析与求解条件讨论

由前面的理论分析与模型求解过程可知，利用单平台上的电子侦察设备对外界已知位置坐标的辐射源目标实施测向，可求解得到平台的位置坐标与姿态参数。实际上这一过程可以从空间解析几何的角度来分析其几何物理意义。在平面几何中圆周角与圆心角具有如下2条性质：

性质1：半径为R的圆中给定一段弦长L，该弦长所对应的圆弧上的任意一个圆周角的度数都是相等的。

性质2：半径为R的圆中，给定一段弦长L，该弦长所对应的圆弧上的圆心角的度数是任意一个圆周角度数的2倍。

上述2条性质可由图3来说明：

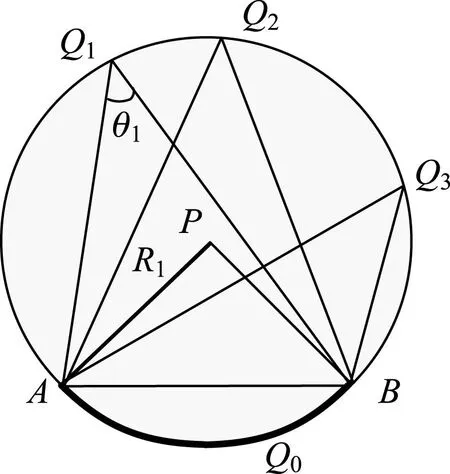
图3　弦长所对应的圆弧上的圆周角与圆心角

图3中圆心为P的圆中弦AB对应的圆弧AQ0B上的圆周角∠AQ1B、∠AQ2B、∠AQ3B都是相等的，且这些圆周角的度数都是圆心角∠APB的度数的一半。所以在给定弦AB的长度lAB和对应的圆周角的大小θ1之后，由性质1和性质2可唯一确定该圆心的位置，且圆的半径R1由下式所表达：

(22)

这意味着在给定三角形的一条边的长度，以及该边所对应的对角的大小之后，这个圆是唯一确定的，且三角形的另一个顶点一定位于由上述参数所唯一确定的圆弧AQ2B上。从三维空间中来观察，将该圆弧以AB为轴在三维空间中进行旋转，即可形成偏轴旋转球面如图4所示。

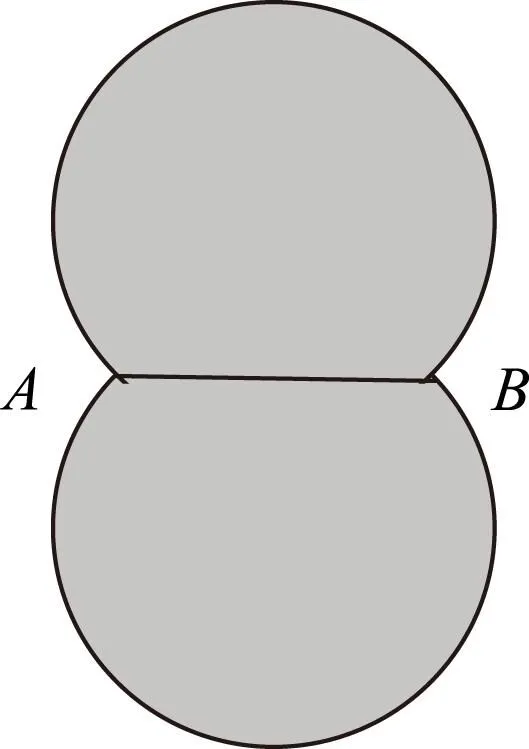
图4　圆弧绕弦长旋转所形成的偏轴旋转球面

于是在三维空间中三角形的顶点将位于这个偏轴旋转球面上。根据前面的应用方式，每两个外界辐射源之间就可以形成一个偏轴旋转球面，两个偏轴旋转球面相交可形成一条曲线，该曲线再与第三个偏轴旋转球面相交所得到的交点即是平台所在位置。

从上述空间解析几何的角度又重新解释了前面位置参数求解的物理意义，这一过程同时也说明：至少需要3个辐射源目标才能得到交点，所以再次印证了前面所说的求解必要条件：要求辐射源目标个数K≥3。但是从上述立体几何分析过程中还可以发现，即使K=3也不一定保证有解，因为当外界辐射源目标位于同一条直线上时，由于图2中的偏轴旋转球面的旋转轴将发生重合，3个旋转球面相交将产生一个圆环，而不是一个交点，从而无法确定顶点的位置，导致方程组无唯一解。

实际上从定位的可观测性来分析，当所有的外界辐射源都位于同一条直线上时，无论被测平台如何运动并实施测量，都无法构成一个空间立体形状，得到的仅仅是一个平面图形，故所获得的解是奇异的。所以在上述求解条件中要求可利用的辐射目标不能位于同一条直线上，只有这样才能确保有唯一解。另一方面，当辐射源目标的数量超过3个时，可利用最小二乘加权求和方式来获得最优解。

5仿真验证

仿真场景：在本地东北天坐标系中，辐射源目标地图中3个辐射源的位置坐标分别为：(8，13，0.1)、(2，30，0.3)、(-12，25，0.2)，单位km(以下同)。一个没有安装惯导和陀螺装置的浮空平台上携带有二维干涉仪测向天线阵，代表平台位置的天线阵中心点处位置坐标的真实值为(6，1，10)，整个天线阵所在的平台的真实姿态参数分别为：航向角-15°(-0.2618 rad)， 俯仰角-10°(-0.1745 rad)，横滚角9°(0.1571 rad)。上述平台位置与姿态参数事先都是未知的，后续通过该天线阵对3个外界辐射源目标进行测向，然后按照前面所述模型可计算得到浮空平台的3个位置估计值与3个姿态估计值，通过计算值与真实值的对比来评估误差。在天线阵所在的坐标系中，测量得到的3个辐射源来波方向上的单位矢量分别为：(0.0028，0.8703，-0.4939)、(-0.3410，0.9157，-0.2148)、(-0.7065，0.6322，-0.3168)。干涉仪的测向精度按0.083°计算。根据前面的位置参数求解模型对式(12)进行迭代求解，其误差收敛曲线如图5所示。收敛之后得到的平台位置坐标为(6.0488，1.0237，9.8703)。

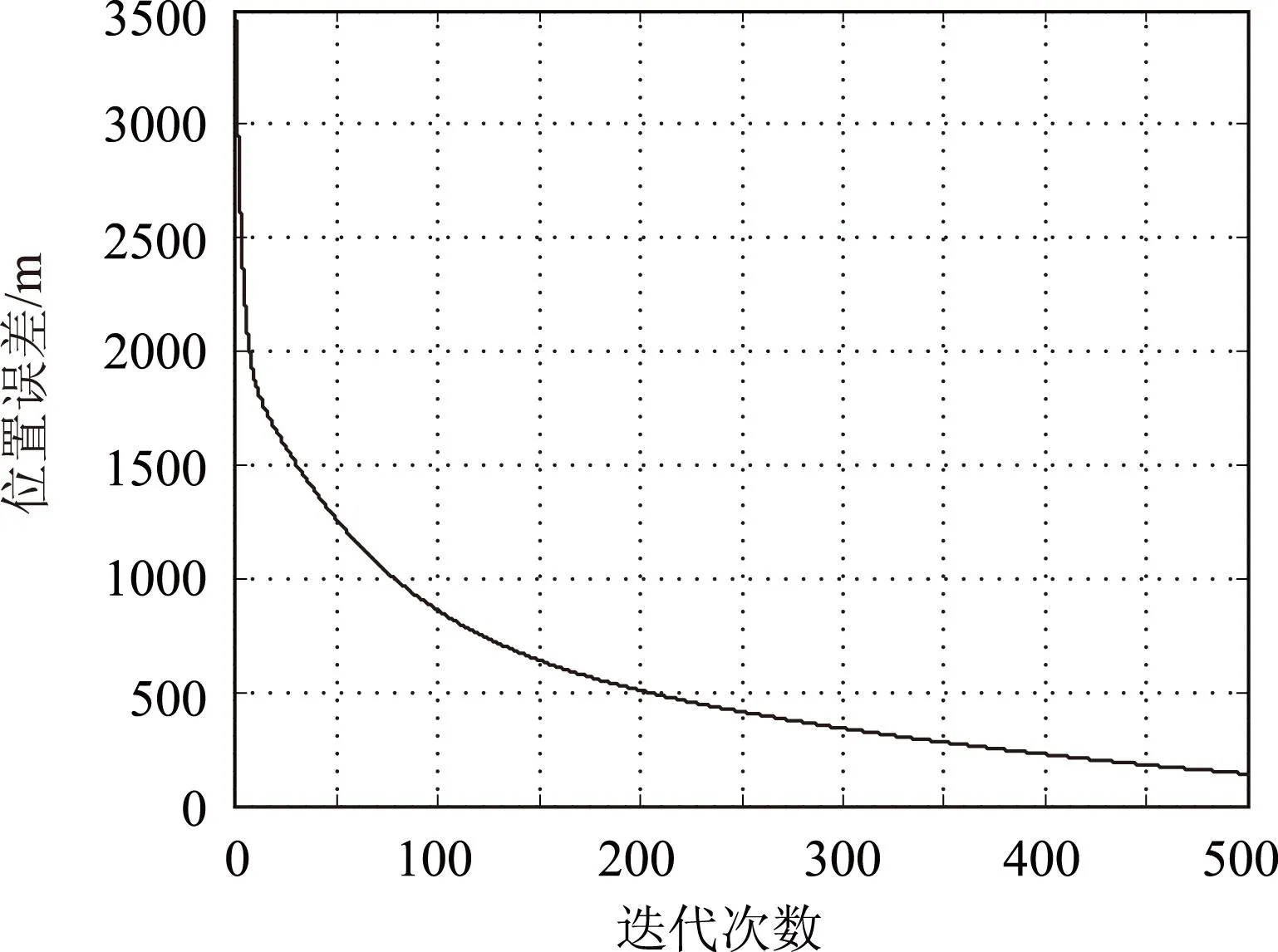
图5　平台位置参数迭代求解的误差收敛曲线

在求解得到平台的位置坐标之后，按照前面的姿态参数求解模型对式(21)进行迭代求解，其总误差收敛曲线如图6所示。收敛之后得到的平台姿态参数为：航向角-14.84°(-0.2590 rad)，俯仰角-9.70° (-0.1694 rad)，横滚角8.99°(0.1570 rad)。

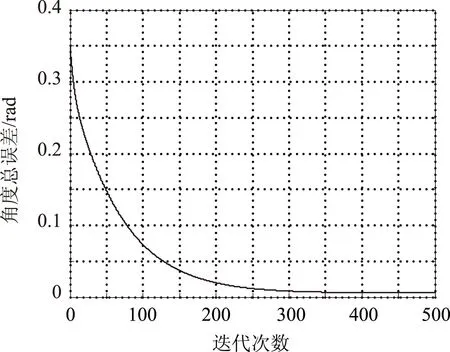
图6　平台姿态参数迭代求解的误差收敛曲线

上述仿真仅仅是其中一次试验所得到的结果，如果经过100次蒙特卡罗仿真，则可以获得平台自定位误差与姿态测量误差的统计曲线如下图所示。

图7　多次仿真得到的平台位置误差曲线

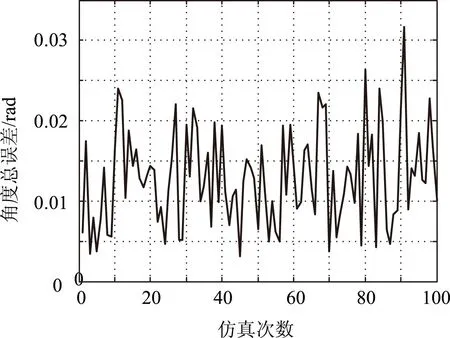
图8　多次仿真得到的平台姿态误差曲线

通过图7与图8的对比可以发现：平台位置误差与姿态测量误差的变化具有大致相同的趋势，即仿真过程中如果位置误差增大时，对应的姿态测量误差也随之增大，其主要原因是姿态估计过程中应用了前面的位置估计的结果。通过统计分析可知，在上述仿真条件下平台自定位的位置误差为355 m，姿态测量的误差为0.0129 rad，即0.739°。

实际上上述误差与平台对辐射源的测向精度是紧密相关的，如果平台上的干涉仪测向精度变差，平台自定位与姿态测量的精度也随之降低。同样在上述仿真条件下，改变干涉仪的测向精度，通过多次蒙特卡罗仿真后统计所得到的平台自定位误差，以及平台的姿态测量误差随干涉仪测向精度的变化曲线如下图所示。

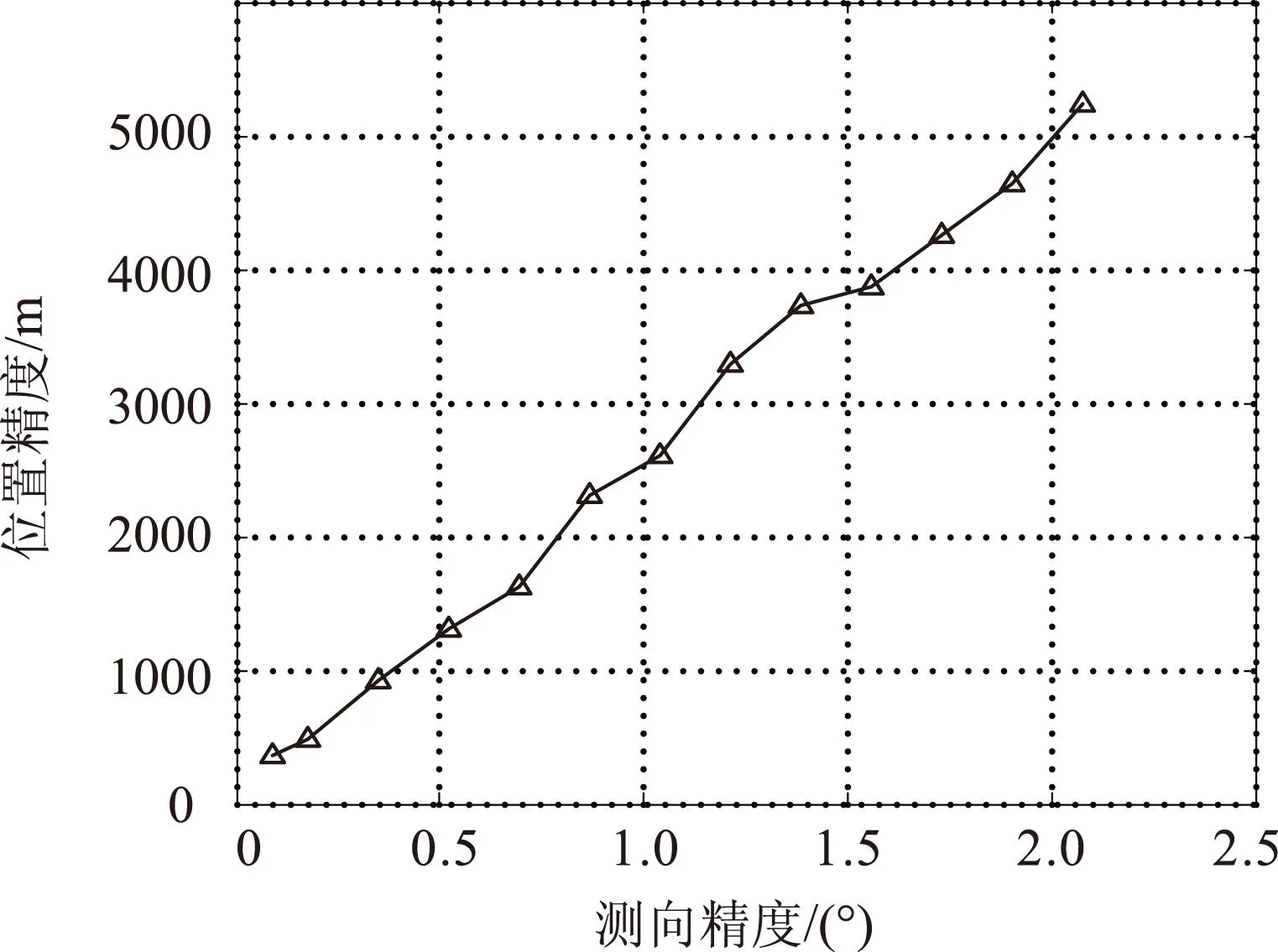
图9　平台位置误差随干涉仪测向精度的变化曲线

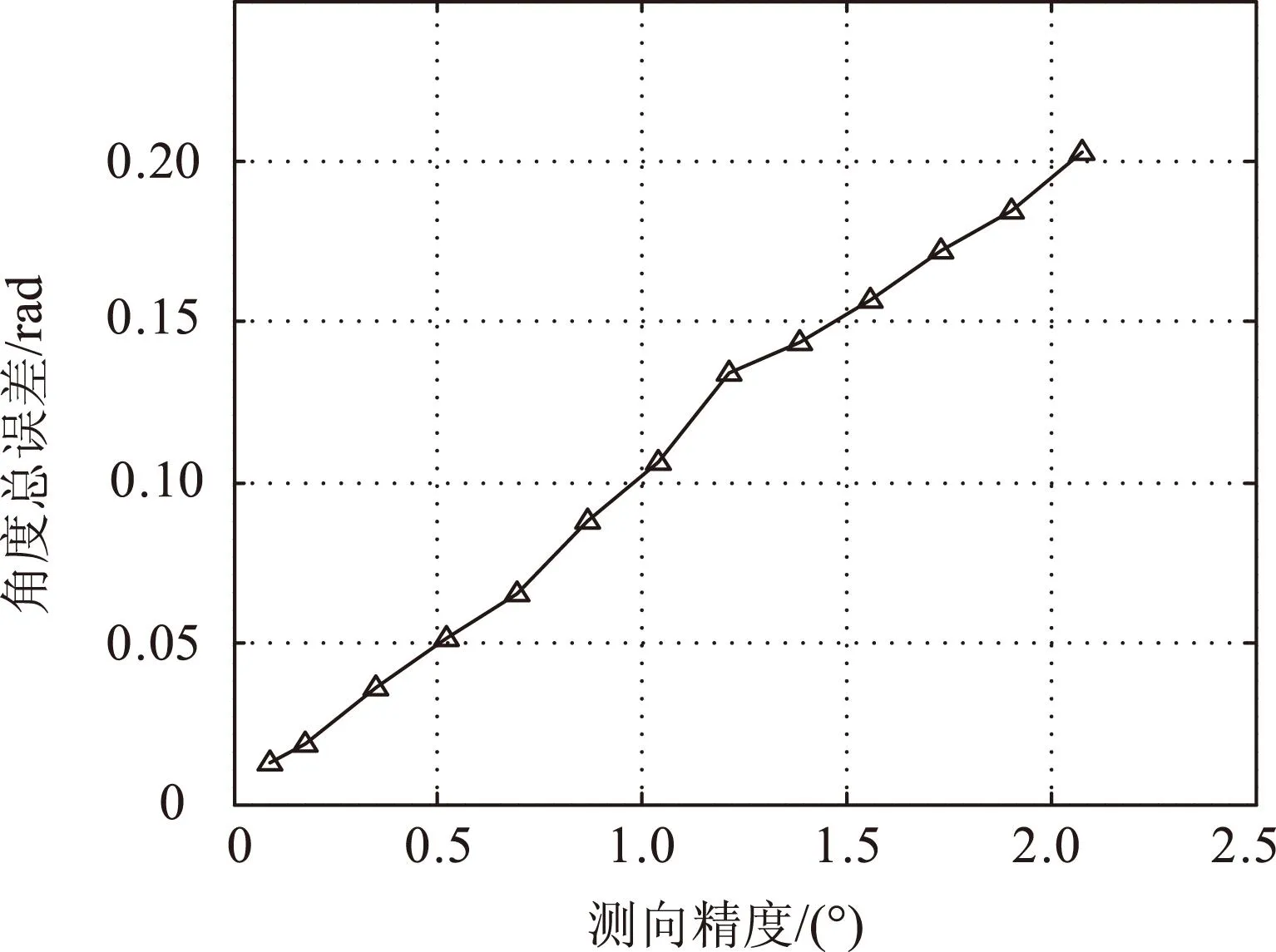
图10　平台姿态误差随干涉仪测向精度的变化曲线

由图9与图10的数据可见，平台的自定位与姿态测量精度随着电子侦察设备对辐射源目标的测向精度的变差而变差，而且呈现出近似的线性变化关系。由上述仿真结果可知：要达到较高的自定位精度和姿态测量精度，对电子侦察的测向精度要求也较高。所以在实际应用中需要对外界辐射源进行优选，选用信号质量好的辐射源作为参考点，以此来尽可能提高对辐射源来波方向的测向精度。

6结语

利用外界多辐射源目标信息的单站导航主要是通过平台上的电子侦察设备对外界已知位置坐标的辐射源目标的来波方向进行测量，获得各个测向角，并以此来求解平台自身的位置坐标与姿态参数。本文参照这一应用方式，首先建立了这一应用问题的数学模型，并巧妙地利用空间几何体在不同坐标系下的各条棱边相对位置的不变性，成功实现了模型中位置参数与姿态参数的解耦与方程组的求解。并从空间解析几何中偏轴旋转圆球面的角度解释了这一问题的几何物理意义，同时也对其求解条件进行了分析讨论。整个模型的正确性与求解过程的有效性得到了仿真结果的验证，从仿真结果中还可以发现：平台的自定位误差和姿态测量误差与对辐射源目标的测向误差近似成线性关系。如要提高平台自定位与测姿的精度，就需要进一步提高平台上的电子侦察设备对外部辐射源目标来波方向的测向精度，所以该导航方式在实际应用过程中，需要根据平台上电子侦察设备性能参数的实际情况对相关的应用条件进行核算，这样才能检验其是否满足各种应用的实际要求。

参考文献：

[1]石荣，邓科，阎剑. 基于逆向无源定位的辐射源目标地图导航[J]. 现代导航，2014, 5(4):239-244.

[2]Elliott D.Kaplan，Christopher J.Hegarty，Understanding GPS principles and applications (Second Edition)[M].USA：MA，Norwood，ARTECH HOUSE，INC. 2006.

[3]Pratap Misra，Per Enge，Global positioning system signals，measurements，and performance[M].USA Massachusetts：Ganga- Jamuna Press，2006.

[4]胡源. 导航战中的GPS干扰研究[J]. 空间电子技术，2009(4)：48-52.

[5]张宁. GPS转发欺骗式干扰应用于无人机的实例分析[J]. 中国航天，2015(7)：40-42.

[6]石荣，易翔，王文松，等. 时延伪GPS卫星干扰的定位控制原理分析[J]. 电子对抗，2007(2)：21-25.

[7]张会锁，高关根，寇磊，等. 利用轨迹诱导的欺骗式GPS干扰技术研究[J]. 弹箭与制导学报，2013，33(3)：149-152.

[8]石荣，邓科. 双站时差测量式辐射源目标地图导航[J]. 现代防御技术，2015，43(4)：68-73，116.

[9]Richard A. Poisel. Target Acquisition in Communication Electronic Warfare Systems [M]. USA, Artech House Inc. 2004.

[10]Richard A. Poisel. Electronic warfare target location methods (second edition) [M]. USA: Artech House Inc., 2012.

石荣(1974—)男，四川人，博士，研究员，主要研究方向为电子对抗，导航定位，通信与雷达系统等；

E-mail：wyx1719@sina.com

姜道安(1965—)男，江苏人，研究员，主要研究方向为电子对抗；

李潇(1993—)女，甘肃人，硕士研究生，主要研究方向为电子对抗。

Platform Self-location and Attitude Measure Technique based on Direction Finding for Radiation Objects

SHI Rong，JIANG Dao-an，LI Xiao

(Science and Technology on Electronic Information Control Laboratory, Chengdu, 610036, China)

Abstract:The navigation based on radiation object map is naturally concealed, staunch and anti-jamming from the outside world. It is an important type of diversity navigation in the intense countermeasure condition of the modern battles. The mathematic model of platform self-location and attitude measure is established for the single station navigation in these applications. The space geometry invariability of the pyramid is utilized in different coordinates. Then location parameters and attitude parameters are novelly decoupled in the equation. In this way the complexity is greatly alleviated and these parameters can be separately gotten successfully. The physical significance of platform self-location and attitude measure based on direction finding for radiation objects is explained from the space analytic geometry. The resolving condition is discussed and its availability is demonstrated by the simulations. It is the important reference for the engineering application of this navigation.

Key words:radiation object map；electronic reconnaissance；direction finding；self-location；attitude measure；inverse passive location；decoupling；diversity navigation

作者简介

中图分类号：TN961/TN971

文献标识码：A

文章编号：1673-5692(2016)01-073-06

基金项目：总装共用技术基金91X0A210XXX1XDZ390XX

收稿日期：2016-01-21

修订日期：2016-02-03

doi:10.3969/j.issn.1673-5692.2016.01.014