基于系统误差的航迹错误关联估计分析

李　洋, 史　伟, 王欣九, 赵尚卓

(1.中国电子科学研究院，北京　100041; 2.南京信息工程大学，南京　210044)

李　洋(1983—)，辽宁锦州人，工程师，主要研究方向为信息融合；

E-mail:seenightrain@qq.com

史　伟(1982—)，山西太原人，高级工程师，主要研究方向为信息融合；

王欣九(1990—)，辽宁锦州人，助理工程师，主要研究方向为信息系统设计；

赵尚卓(1988—)，山西省长治人，硕士研究生，主要研究方向为信息处理。



工程与应用

基于系统误差的航迹错误关联估计分析

李洋1, 史伟1, 王欣九1, 赵尚卓2

(1.中国电子科学研究院，北京100041; 2.南京信息工程大学，南京210044)

摘要：航迹关联是多传感器数据融合处理的关键问题。系统误差的存在给航迹关联带来困难，并产生大量的错误关联对。系统误差与航迹关联具有内在的联系，分析系统误差在航迹错误关联中所起作用将有助于对航迹错误关联的检测。本文通过系统误差残差的统计规律，利用高斯和卡方检测器分析了传感器虚警航迹、传感器方位向系统误差、传感器距离向系统误差等因素对于航迹错误关联检测率的影响，展示出了系统误差在航迹关联错误检测过程中所起的作用。

关键词：航迹关联; 航迹融合; 系统误差; 高斯检测器; 卡方检测器

0引言

多传感器航迹融合已经在军民等领域取得了广泛的应用。对于比较常用的分布式数据融合系统，每个传感器都接收大量的目标航迹信息，融合中心将目标航迹信息进行融合[1-2]。航迹关联可以判定不同传感器的不同航迹是否是对相同目标进行跟踪，解决了传感器空间覆盖区域内部的目标重复跟踪问题，变相地也完成了不同目标区分的功能[3-4]。

准确的航迹关联可以提高目标状态信息估计精度，提高目标跟踪精度等。而航迹的错误关联将使得航迹融合结果不准确，影响目标状态和跟踪精度的降低，甚至导致航迹不可用[5]。

在实际应用中，量测噪声的相关性、目标密集程度、时刻配准、传感器系统误差等都对航迹关联结果产生干扰，导致传感器目标跟踪存在较大误差，给航迹关联带来很大困难。而这些影响因素中，传感器系统误差的影响最为严重，并已经引起了大量研究人员的关注。

文献[6]给出了匹配算法对航迹关联中系统误差估计结果。文献[7]指出了错误关联会造成融合结果的混乱，可用性降低。文献[8]解释了航迹关联不确定度与信息不确定性的香农熵度量和哈特利度量之间的关系，提出了航迹关联不确定度评定方法。

文献[9]提出了用于关联误差检测的高斯和卡方检测器。本文在文献[9]的基础上，利用系统误差与航迹关联的耦合关系，分析了传感器虚警、检测概率、系统误差偏移期望等参数对于航迹错误关联检测的影响，理论成果为建立系统误差与航迹错误关联检测之间的非线性关系提供有价值的参考。

1问题的数学描述

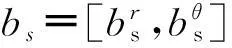
1.1传感器系统误差模型

(1)

(2)

(3)

1.2航迹关联与系统误差

存在系统误差的航迹关联中，航迹关联和传感器相对系统误差是存在内在联系的。在对传感器的系统误差进行估计时，需要考虑航迹关联；相反，对航迹进行关联同时，也要考虑系统误差的影响。

(4)

将公式(3)带入到方程(4)中可以得到如下的表达形式：

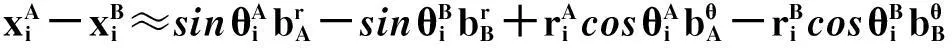
(5)

(6)

(7)

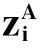
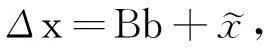
(8)

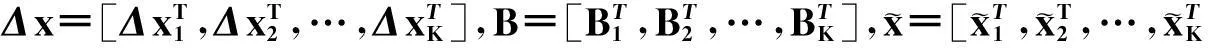
2航迹错误关联检测

通过ri满足均值为mi，协方差为Pi的正态分布的假设，可以得到高斯关联检测器(GD)如下：

其中T1为检测门限。

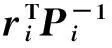
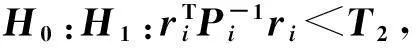
如果高斯和卡方检测器系统误差残差是通过系统误差真值得到的，则称为给定门限下的最优高斯检测器(optGD)和最优卡方检测器(optCD)。

3仿真结果分析

为对本文描述的仿真方法进行比较和分析，设置如下的仿真环境。

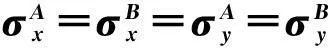
3.1场景一

设传感器A和B的虚警航迹数均服从于均值从1到3以0.1为步长的泊松分布，漏报率为0.1，传感器A和B的系统误差在距离向分别为0.1 km和-0.1 km，方位向分别为0.3°和-0.3°。仿真结果如图1所示。

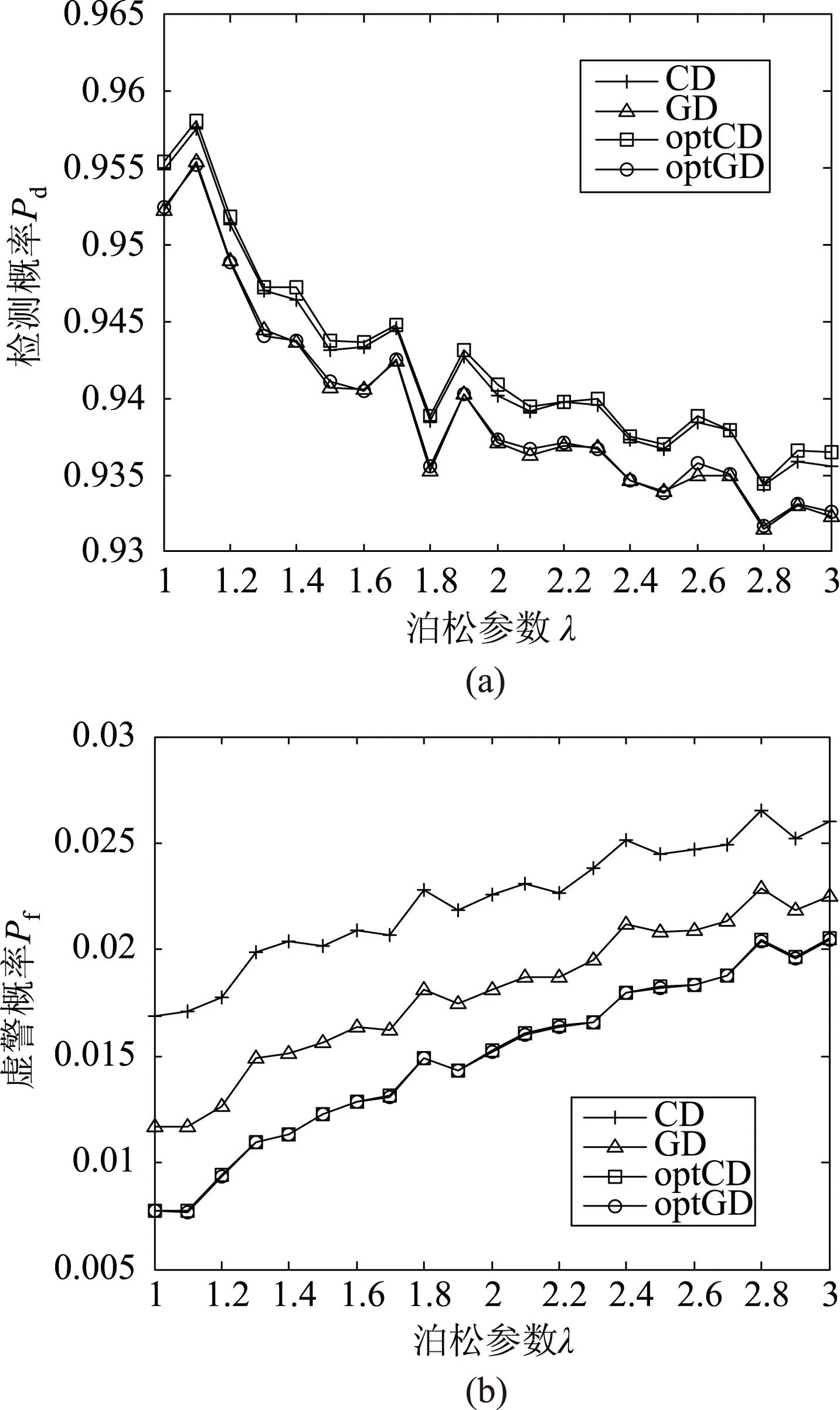
图1　关于不同泊松参数λ的检测概率(a)和虚警概率(b)

从图1中可以看出，随着泊松参数λ的增加，检测概率逐步降低，虚警率逐步增加。无论是CD还是optCD，检测概率都要大于相应的GD和optGD，所以当传感器间虚警航迹数满足于泊松分布时，推荐使用CD检测器。

3.2场景二

设传感器A和B的虚警航迹数均服从于均值从2的泊松分布，漏报率为0.1，传感器A和B的系统误差在距离向分别为0.1km和-0.1 km，但是设传感器A方位向系统误差为[0.05°,1°],步长为0.05°，传感器B方位向系统误差为-0.3°。仿真结果如图2所示。

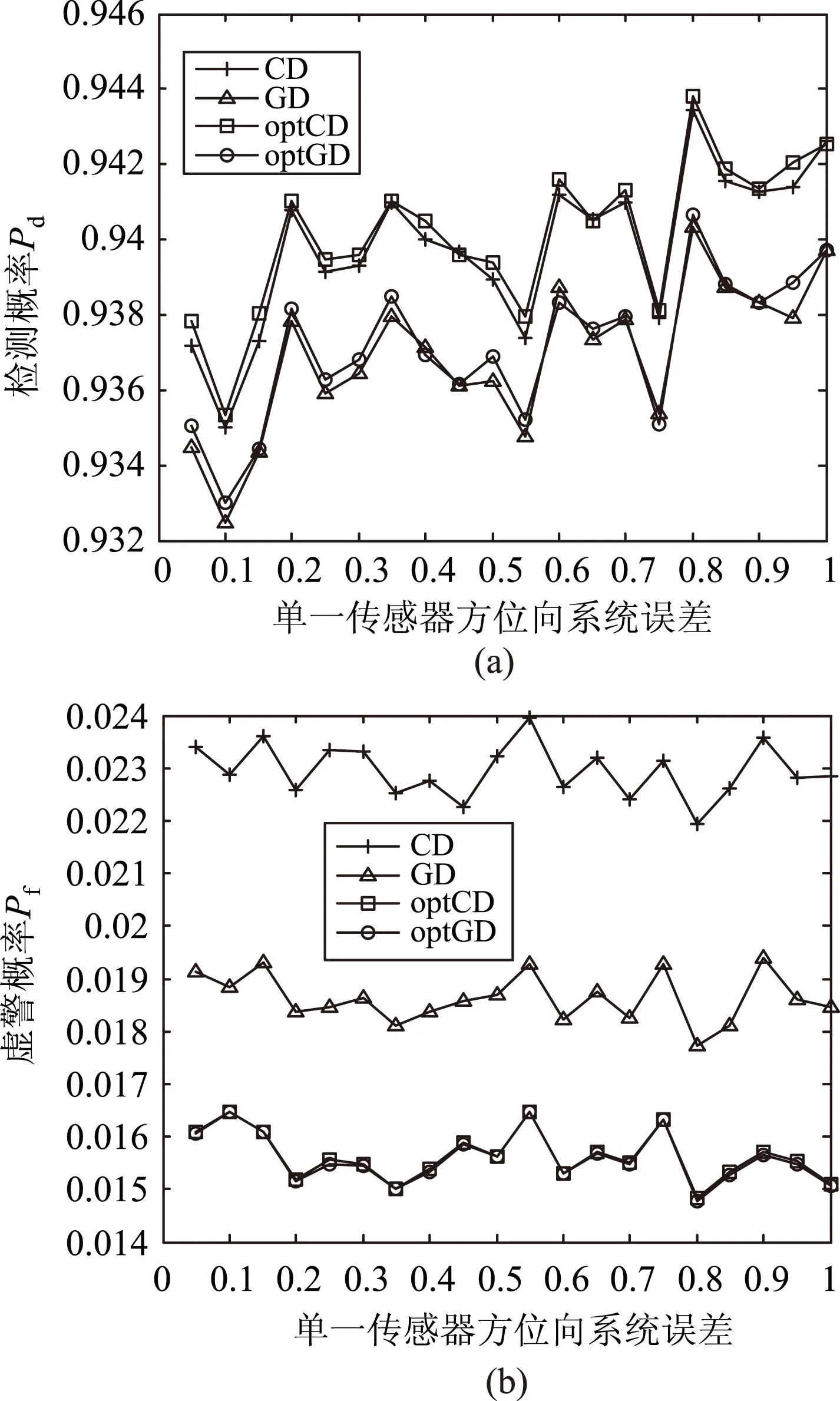
图2　关于单一传感器A方位向系统误差的(a)检测概率和(b)虚警概率

图2与图1相比，检测概率和虚警概率随着单一传感器A方位向误差的变化并不明显，但是不同算法之间的性能相差还是很明显的。从图2中可以看出随着单一传感器A的方位误差的变化，CD和optCD要普遍大于GD和optGD,但是CD和optCD及GD和optGD之间的性能相似，接近于相等。虚警概率GD和optGD要小于optCD，也要小于CD检测器。所以当单一传感器方位向具有明显噪声时，推荐使用CD和optCD检测器而optCD要优于CD检测器。

3.3场景三

设传感器A和B的虚警航迹数均服从于均值从2的泊松分布，漏报率为0.1，传感器A和B的系统误差在距离向分别为0.1 km和-0.1 km，同时设两个传感器A和B方位向系统误差为[0.05°,1°]和-[1°,0.05°],步长同为0.05°。仿真结果如图3所示。

图3　两个传感器AB方位向系统误差同时变化对应的(a)检测概率和(b)虚警概率

图3将图2的单一传感器方位向具有变化的系统误差扩展到了两个传感器同时具有变化的方位向误差，性能结果也具有相似的结论，即随着两个传感器A和B的方位误差的同时相同变化，CD和optCD检测概率要普遍大于GD和optGD,但是CD和optCD及GD和optGD之间的性能接近于相等。虚警概率GD和optGD要小于optCD和CD检测器。所以当两个传感器同时在方位向上具有明显噪声时，也推荐使用CD和optCD检测器，而optCD要优于CD检测器。

3.4场景四

设传感器A和B的虚警航迹数均服从于均值从2的泊松分布，漏报率为0.1，传感器A距离向系统误差在[0.01km,0.2km]，步长为0.01km，传感器B距离向系统误差为-0.1km，同时设两个传感器A和B方位向系统误差分别为0.30和-0.30。仿真结果如图4所示。

图4　单一传感器A距离向系统误差对应的(a)检测概率和(b)虚警概率

图4与图2和图3相似，检测概率和虚警概率随着单一传感器A距离向误差的变化并不明显，性能区别主要集中在不同算法之间。从图4中可以看出随着传感器A的距离向误差的变化，CD和optCD同样大于GD和optGD, CD和optCD及GD和optGD之间接近于相等。虚警概率GD和optGD要小于optCD，也要远小于CD检测器。所以当单一传感器距离向具有明显噪声时，推荐使用CD和optCD检测器，而optCD要略微优于CD检测器。

3.5场景五

设传感器A和B的虚警航迹数均服从于均值从2的泊松分布，漏报率为0.1，传感器A和B距离向系统误差分别为[0.01km,0.2km]和[-0.2km,-0.01km]，步长同为0.01km，同时设两个传感器A和B方位向系统误差分别为0.3°和-0.3°。仿真结果如图5所示。

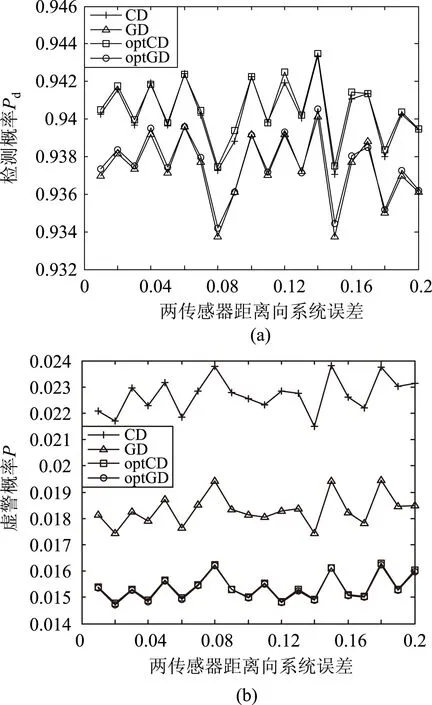
图5　两传感器AB距离向系统误差同时变化对应的(a)检测概率和(b)虚警概率

图5与图4极为相似，说明距离向的系统误差相对于单个传感器和多个传感器对于错误关联检测几乎没有影响。如图5所示，CD和optCD的检测概率同样大于GD和optGD,CD和optCD及GD和optGD之间接近于相等。虚警概率GD和optGD要小于optCD，也要远小于CD检测器。所以当两个传感器的距离向同时具有明显噪声时，推荐使用CD和optCD检测器，而optCD也要略微优于CD检测器。

4结语

本文对传感器量测虚警航迹数分布、单一传感器在距离向和方位向的系统误差、两个传感器同时距离向和方位向具有系统误差等因素对航迹错误关联检测的检测概率和虚警概率的影响进行了研究，得到如下结论：1.在错误关联检测率方面，CD检测器要相对于GD检测器具有优势；2.在虚警率方面GD检测器相对于CD检测器具有优势。在以后的研究中，将主要集中在利用实测量测数据对算法结论进行验证，同时给出更加准确的错误误差偏差模型[10-11]。

参考文献：

[1]何友, 王国宏等. 多传感器信息融合及应用(第二版)[M]. 北京: 电子工业出版社, 2007.

[2]韩崇昭, 周彬等. 共同杂波环境下多目标量测数据的误差传递与校正[J]. 自动化学报, 2007, 33(7): 771-774.

[3]张晶等. 集中交互式多传感器模糊联合概率数据互联算法[J] . 电子学报, 2008, 36(8): 1655- 1659.

[4]林洪桦. 测量误差与不确定度评估[M]. 北京: 机械工业出版社, 2010.

[5]王增福, 潘泉, 梁彦. 一种基于自适应杂波密度模型的OTHR Viterbi数据关联跟踪算法[J]. 系统科学与数学, 2010, 30(6): 752- 760.

[6]杜雄杰, 王钺, 山秀明. 系统误差环境下二维分配算法的关联性能[J]. 清华大学学报(自然科学版), 2012, 52(5): 616-622.

[7]Kessel R T. The dynamics of information fusion: synthesis versus misassociation [C]// Proceeding of the International conference on Information Fusion, 2006: 1-6.

[8]陈世友, 肖厚, 刘颢. 航迹关联不确定度的表示[J]. 电子学报, 2011, 39(7): 1589-1593.

[9]田威, 王钺, 山秀明, 杨健. 基于系统误差估计残差的错误关联检测方法[J]. 系统工程与电子技术, 2013, 35(10): 2065-2068.

[10]李洋, 张靖, 石教华, 张晓丽. 目标航迹融合质量度量方法研究. 中国电子科学研究院学报, 2015, 10(3): 254-259.

[11]张永利, 刘春旭. 基于Vague集TOPSIS法的防空战场信息感知系统效能评估[J]. 中国电子科学研究院学报, 2013, 8(4): 373-376.

李洋(1983—)，辽宁锦州人，工程师，主要研究方向为信息融合；

E-mail:seenightrain@qq.com

史伟(1982—)，山西太原人，高级工程师，主要研究方向为信息融合；

王欣九(1990—)，辽宁锦州人，助理工程师，主要研究方向为信息系统设计；

赵尚卓(1988—)，山西省长治人，硕士研究生，主要研究方向为信息处理。

The Analysis of Track Mis-association Evaluation Based on the System Bias

LI Yang, SHI Wei, WANG Xin-jiu, ZHAO Shang-zhuo

(1.China Academy of Electronics and Information Technology, Beijing 100041, China;2.Nanjing University of Information Science & Technology, Nanjing 210044, China)

Abstract:Track association plays an important role in the data fusion for the multi- sensors. System bias brings lots of difficulties and mis-association for the track association. System bias and track association have the inherent relation, thus the track mis-association can be detected from the effect of system bias on the track mis-association. In the paper, we analyzed the role of sensor false track, sensor azimuth bias, and sensor range bias on the detection of track mis-association by the Gaussian and Chi-square detectors based on the statistics of system bias. At last, we showed the comparison of track mis-association detection and the system bias with the different detectors.

Key words:track association; track fusion; system bias; Gaussian detector; Chi-square detector

作者简介

中图分类号：TP277/TN919.3+3

文献标识码：A

文章编号：1673-5692(2016)01-040-05

基金项目：国家自然科学基金(41076119)

收稿日期：2015-11-12

修订日期：2016-01-16

doi:10.3969/j.issn.1673-5692.2016.01.009