浅谈计量测量中的系统误差
2015-10-12张付山
■文/张付山
浅谈计量测量中的系统误差
■文/张付山

测量误差是计量测试的一个基本问题,受到了日益广泛的重视,长期以来,人们又比较习惯于应用系统误差的概念,近年来,大家普遍认为,“不确定度”似比“误差”更为合适,通常所谓的误差,实际上都是指测量结果的可能误差范围或误差限即“不确定度”。
而测量误差是指测得值与真值之差。严格来讲,被测量的绝对值永远是未知的,但随着科技的发展,测试方法和手段的不断改进,人们对真值的认识逐渐加深,即越来越接近绝对真值,因此,我们通常所说的真值,实际上都是相对真值。
根据性质测量误差可分为三类:系统误差、随机误差、粗大误差。下面浅谈一下计量测量中的系统误差:
系统误差的概念
在一定条件下,重复测量同一量时,始终恒定或按一定规律变化的误差称为系统误差。系统误差决定测量结果的“正确”程度。
许多系统误差可通过实验确定(或根据实验方法、手段的特性估算出来)并加以修正。但有时由于对某些系统误差的认识不足或没有相应的手段予以充分确定,而只能给出一个误差范围,即所谓的未定或剩余系统误差,亦称未消除的系统误差。
显然,系统误差与测量次数无关,亦不能用增加测量次数的方法使其消除或减小。系统误差按其呈现特征可分为常值系统误差和变值系统误差,而变值系统误差又可分为累积的、周期的和按复杂规律变化的系统误差。
系统误差的发现方法
在精密测量中,对比较显著的系统误差,应细致敏锐地查找其产生的原因和变化规律,否则不但不能对系统误差进行修正和消除,甚至还不知道是否有误差存在。尤其是变值系统误差,它将歪曲随机误差的分布规律,使其对随机误差不能进行正确的分析和估算,故应引起高度重视。
下面介绍一些如何从测得结果的数据中分析发现系统误差的方法:
定值系统误差不影响测得值的残余误差,它对重复测量的每一结果的影响相同,故从测量列的原始数据本身看不出有无定值系统误差存在,但可用以下方法来发现。
1.对比检定法
要判断某一测量条件下是否有定值系统误差,在确信没有明显变值系统误差的前提下,可以改用更好的测量条件(如改用更高精度的仪器或基准),进行检定性测量。以此两种不同的测量条件对同一量值进行次数相同的重复测量,求出两者算术平均值之差,则此差值即为该被判断的测量条件下的定值系统误差,因为两种不同测量条件具有相同的系统误差的可能性是很小的。
2.均值与标准偏差比较法
对同一量值在测量条件不同、测量次数也不同的情况下进行两组(或多组)测量,设测量次数分别为n1和n2次,得两组平均值和为:x1和x2为:
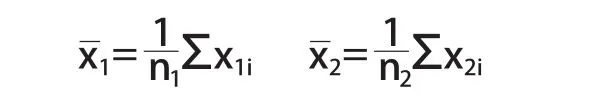
如果测量条件稳定,没有明显的变值系统误差,且都服从正态分布,则两列测得值的分布中心(数学期望)均将为理论均值μ,而x1和x2都将为近似值μ,因为x1和x2也是随机变量,所以两者之间总会有些差异。根据x1和x2的近似程度,结合两者差异发生的概率,便可大致确定两组测得值是只含有随机误差,还是也伴有定值系统误差存在。
两列测得值的方差估计值为:
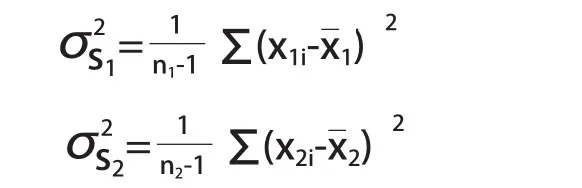
平均值和方差估计值为:
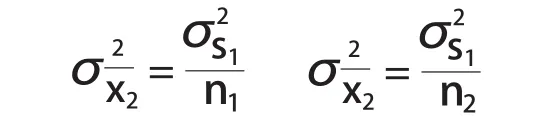
两平均值之差的方差为:

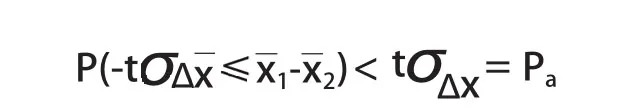
为与对应的概率值,也可写成
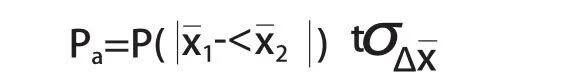
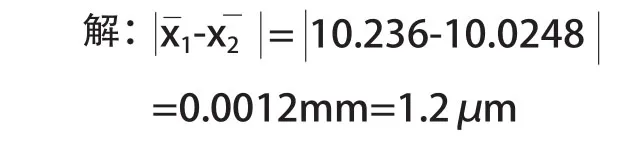
此两平均值之差的标准偏差为:

按正态分布,如取置信概率为99%,则t=2.58,故:

故有根据判断两组测得值(或其中一组)含有定值系统误差,应查找根源并予以消除或修正。
当测量次数n1和n2较少时,可按t分布来判断。

式中,(n1+n2-2)为自由度。
系统误差的消除系统处于某个工作状态,然后以已知量替代之,并使系统的工作状态保持不变。例如,利用电桥测量电阻、电感和电容等。
(2)补偿法:通过两次不同的测量,使测量值的误差具有相反的符号,然后取平均值。例如:用正反向二次测量来消除热电转换器的直流正反向差。
(3)对称法:当被测量为某量(如时间)的线性函数时,距相等的间隔依次进行数次测量(至少三次),则其中任何一对对称观测值的累积误差的平均值皆等于与两次观测的间隔中点相对应的累积误差t,即
根据上述产生系统误差的种种原因,不难得出下列一些消除系统误差的基本方法。
1.测量前设法消除可能消除的误差源。
2.测量过程中采用适当的实验方法,如替代法、补偿法、对称法等,将系统误差消除。
(1)替代法:用与被测对象处于相同条件下的已知量来替代被测量,即先将被测量接入测试回路,使利用这一对称性便可将线性累积系统误差消除。
3.通过适当的计算对测量结果引入可能的修正量。
4.通过若干人的重复测量来消除人员误差。
需要指出,在具体测量中,往往很难将系统误差完全消除。因此,应力求比较确切地给出残余系统误差的范围,即未消除的系统误差限。
天津市宁河县计量检定所)

