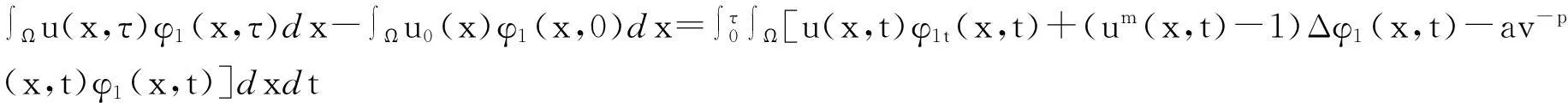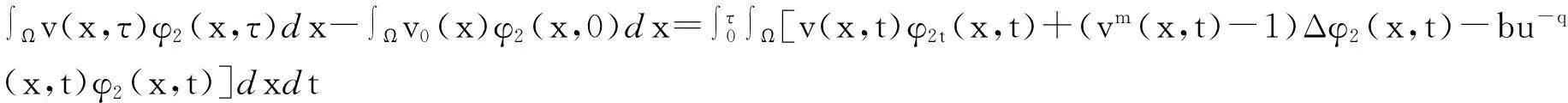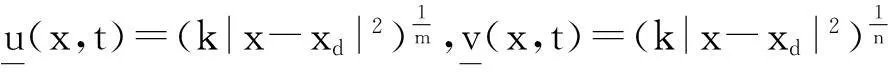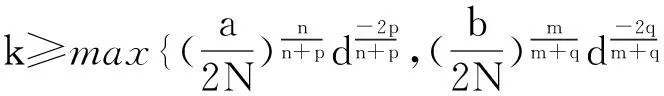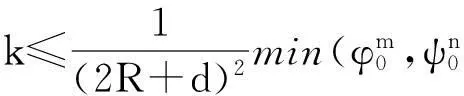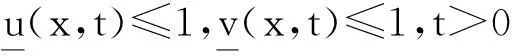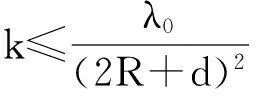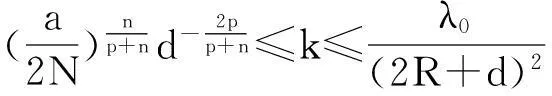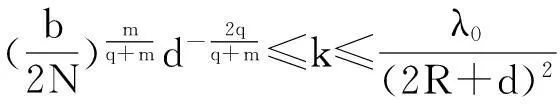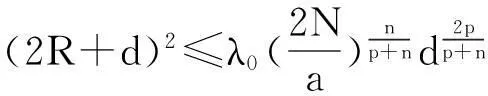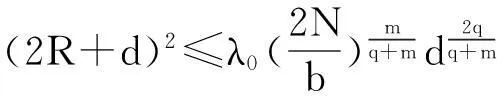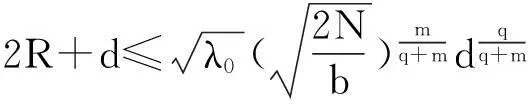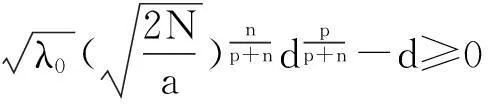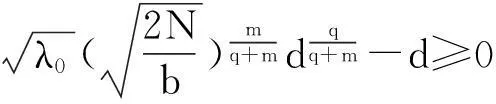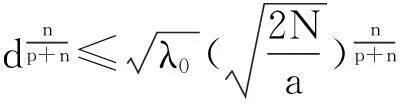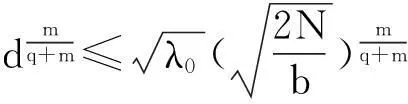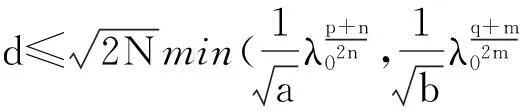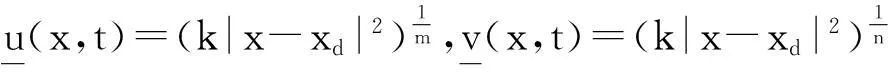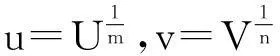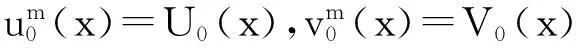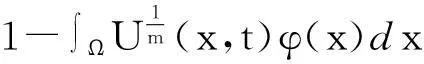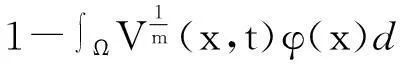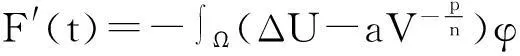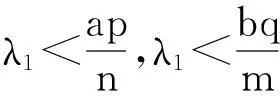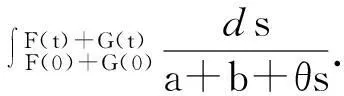一类退缩反应扩散方程组的整体解的存在性与猝灭

孙仁斌

(中南民族大学 数学与统计学学院，武汉 430074)



一类退缩反应扩散方程组的整体解的存在性与猝灭

孙仁斌

(中南民族大学 数学与统计学学院，武汉 430074)

摘要分析了一类退缩反应扩散方程组的初边值问题，讨论了此方程组整体解存在的条件，证明了当区域Ω的直径适当小时，解是全局存在的；当Ω的直径适当大时，解会在有限时刻发生猝灭现象，得到了Ω直径的量化范围．

关键词退缩反应扩散方程组；整体解；有限猝灭时间；区域直径

Existence and Quenching of Global Solution for A Class of Degenerate Reaction Diffusion System

SunRenbin

(College of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074,China)

AbstractIn this paper, initial-boundary value problem of a class of degenerate reaction diffusion system was analyzed, and existence conditions of global solution of this system were discussed. It was proved that the global solutions exist while the diameter of regionΩis adequate small, yet the solutions would quench in a finite time while the diameter ofΩis adequate large. The range of diameter ofΩwas obtained.

Keywordsdegenerate reaction diffusion system；global solution；finite quenching time；the diameter of region

本文讨论如下退缩反应扩散方程组的初边值问题：

其中Ω是N维空间中具有光滑边界的有界区域，常数a,b,p,q为正实数,m,n>1,u0(x),v0(x)是连续函数，0

问题(1)中方程的右边含有奇异项av-p，bu-q，其解可能会发生所谓的猝灭现象．关于猝灭问题的研究，最早由Kawarada在文[1]中提出，此后大量的研究得以展开[2-6]，其中所讨论的问题大都只涉及到半线性方程或非退化的拟线性方程，其基本结论是：当区域Ω充分小时，问题的解整体存在；当区域Ω充分大时，解会在有限时刻发生猝灭．随着研究的深入，对于反应扩散方程组的猝灭现象，近年来有了一些结果[7-9]，而对于退缩方程的研究，也开始有人涉及[10-13]．

本文对问题(1)的讨论进一步深化，是关于两个函数耦合的退缩方程组的初边值问题，先通过上下解方法给出系统的解整体存在时区域Ω的直径应满足的一个充分条件，再讨论解在有限时刻发生猝灭时Ω应满足的充分条件．

1解的存在性

由于问题(1)中的方程为退缩的，经典的抛物方程理论中关于解的存在性的讨论方法在此并不适用，我们需要讨论该问题弱解的存在性，为此先给出问题(1)弱解的定义．

(2)

则称u(x,t),v(x,t)为问题(1)的弱解．

如果对任意T>0，方程的弱解都存在，则称弱解为整体存在．

关于退缩抛物型方程组弱解的局部存在性，有多种方法可以得到[11,12]，一般都是先构造一个非退缩抛物方程组的初边值问题的序列，再通过逐步逼近的方法来得到，限于篇幅，本文在此略去．

下面讨论问题(1)整体解的存在性，我们采用的上、下解方法在很多讨论非退缩方程古典解的存在性时经常用到，而对于退缩方程组，需要做一些补充，为此，先给出问题(1)上、下弱解的定义．

对于退缩方程组初边值问题的弱解，与古典解一样，下面的比较原理和存在性定理仍然成立，证明方法可参考文[12]．

根据定理1，为了得到问题(1)解的整体存在性，我们只需找到它的一对整体存在的上、下解即可．

为了叙述方便，假设Ω是以原点O为中心，R为半径的球形区域：Ω=B(O,R)，当Ω是其它形状的区域时，可用同样方法得到本文的结论．

(3)

(4)

(5)

为使(3)、(5)式同时成立，须：

或

(6)

上式右端应为正数，故必须有：

或

即：

(7)

由此可得定理2．

定理2设常数d满足条件(7)，则当区域Ω的半径R满足(6)式时，问题(1)的解是整体存在的．

2解的猝灭性

则问题(1)转化为如下关于U(x,t),V(x,t)的初边值问题：

(8)

设λ1与φ(x)是如下特征值问题的第一特征值与相应的特征函数：

(9)

则λ1>0，且x∈Ω时，φ(x)>0，我们假设∫Ωφ(x)dx=1，令：

利用问题(8)中的方程，我们有：

利用Jensen不等式，有：

F′(t)+G′(t)≥a+b+(bq-mλ1)F(t)+

(ap-nλ1)G(t).

(10)

根据上面的分析，可以得到定理3．

参考文献

[1]Kawarada H．On solutions of initial-boundary value problem forut=uxx+1/(1-u)[J]. Publ Res Inst Math Sci, 1975,10：729-736.

[2]Guo J S．On the quenching behavior of the solution of a semilinear parabolic equation[J]. J Math Anal Appl,1990,151：58-79.

[3]Dai Q Y，Gu Y G．A short note on quenching phenomena for semilinear parabolic equations[J]. J Differential Equations, 1997,137：240-250.

[4]Salin T．On quenching with logarithmic singularity[J]. Nonlinear Analysis,2003,52：261-289．

[5]Bertdch M, Ughi M．Positivity peoperties of viscosity solutions of a degenerate parabolic equation[J].Nonlinear Analysis,1990,14：571-592．

[6]孙仁斌．含有对数奇异项的抛物方程解的整体存在性与猝灭性[J]．江西师范大学学报(自然科学版)，2006,30(4)：307-310．

[7]Pablo A, Quiros F, Rossi J D．Non-simultaneous quenching[J]. Appl Math Lett, 2002,15：265-269．

[8]Ferreira R，Pablo A，Quiros F．Non-simultaneous quenching in a system of heat equations coupled at the boundary[J]．Z Angew Math Phys, 2006,57：586-594．

[9]Zheng Sining, Wang Wei．Non-simultaneous versus simultaneous quenching in a coupled nonlinear parabolic system[J]．Nonlinear Analysis, 2008,69：2274-2285．

[10]Winkler M．Quenching phenomena in strongly degenerate diffusion equations with strong absorption[J]. J Math Anal Appl，2003,288：481-504．

[11]Winkler M．Infinite-time quenching in a fast diffusion equation with strong absorption[J]. Nonl Diff Equ Appl, 2009,16：41-61．

[12]Yang Ying，Yin Jingxue，Jin Chunhua．A quenching phenomenon for one-dimensionalp-laplacian with singular boundary flux[J]．Appl Math Lett, 2010,23：955-959．

[13]孙仁斌．含有奇异项的退缩抛物方程解的整体存在性与有限时刻猝灭性[J]．中南民族大学学报(自然科学版)，2013，32(1)：102-105．

[14]Anderson J R．Local existence and uniqueness of solutions of degenerate parabolic equations [J].Comm Partial Differential Equations,1991,16：105-143．

[15]Aronson D G, Crandall M, Peletier L A．Stabilization of solutions of a degenerate nonlinear diffusion problem[J].Nonlinear Analysis,1982,6：1001-1022．

[16]Anderson J R, Deng K．Global existence for degenerate parabolic equations with a non-local forcing[J].Methods Appl Sci,1997,20：1069-1087．

中图分类号O175.26

文献标识码A

文章编号1672-4321(2016)01-0141-04

基金项目国家自然科学基金资助项目(61374085) 国家自然科学基金资助项目(11301552)；中南民族大学研究生创新基金资助项目(2016sycxjj135)

作者简介孙仁斌(1964-)，男， 副教授，研究方向：抛物型偏微分方程，E-mail：sunrenbin@foxmail.com 夏永波(1979-)，男，副教授，博士，研究方向：编码与密码学，E-mail:xia@mail.scuec.edu.cn

收稿日期2016-02-21 2015-12-03