基于蚁群算法的无联系并行机调度问题的仿真研究

王文涛，穆晓峰，王玲霞

(中南民族大学 计算机科学学院，武汉 430074)



基于蚁群算法的无联系并行机调度问题的仿真研究

王文涛，穆晓峰，王玲霞

(中南民族大学 计算机科学学院，武汉 430074)

摘要针对无联系并行机调度求解问题，引入了蚁群算法的思想.基于转移概率构建的信息素迭代模型，研究了无联系并行机调度问题的求解过程.基于Python的仿真实验结果表明：通过蚁群算法可以得到其近似解；更进一步探求了任务次序对解的影响；通过实验探索了此算法的时间性能.

关键词并行机；任务调度；蚁群算法

Study on Unrelated Parallel Machine Scheduling Problem Based on the Ant Colony Algorithm

WangWentao,MuXiaofeng,WangLingxia

(College of Computer Science, South-Central University for Nationalities,Wuhan 430074,China)

AbstractAiming at unrelated parallel machine scheduling problem, we introduced the idea of ant colony algorithm. Based on pheromone iterative model constructed by transfer probability, we researched the solving process of unrelated parallel machine scheduling problem. The results of the simulation test based on Python illustrate that ant colony algorithm can reach an approximate solution. Furthermore, we explored the influence of different task sequence on solution. At last, we performed some experiment to analyze time performance of the algorithm.

Keywordsparallel machine；task scheduling；ant colony algorithm

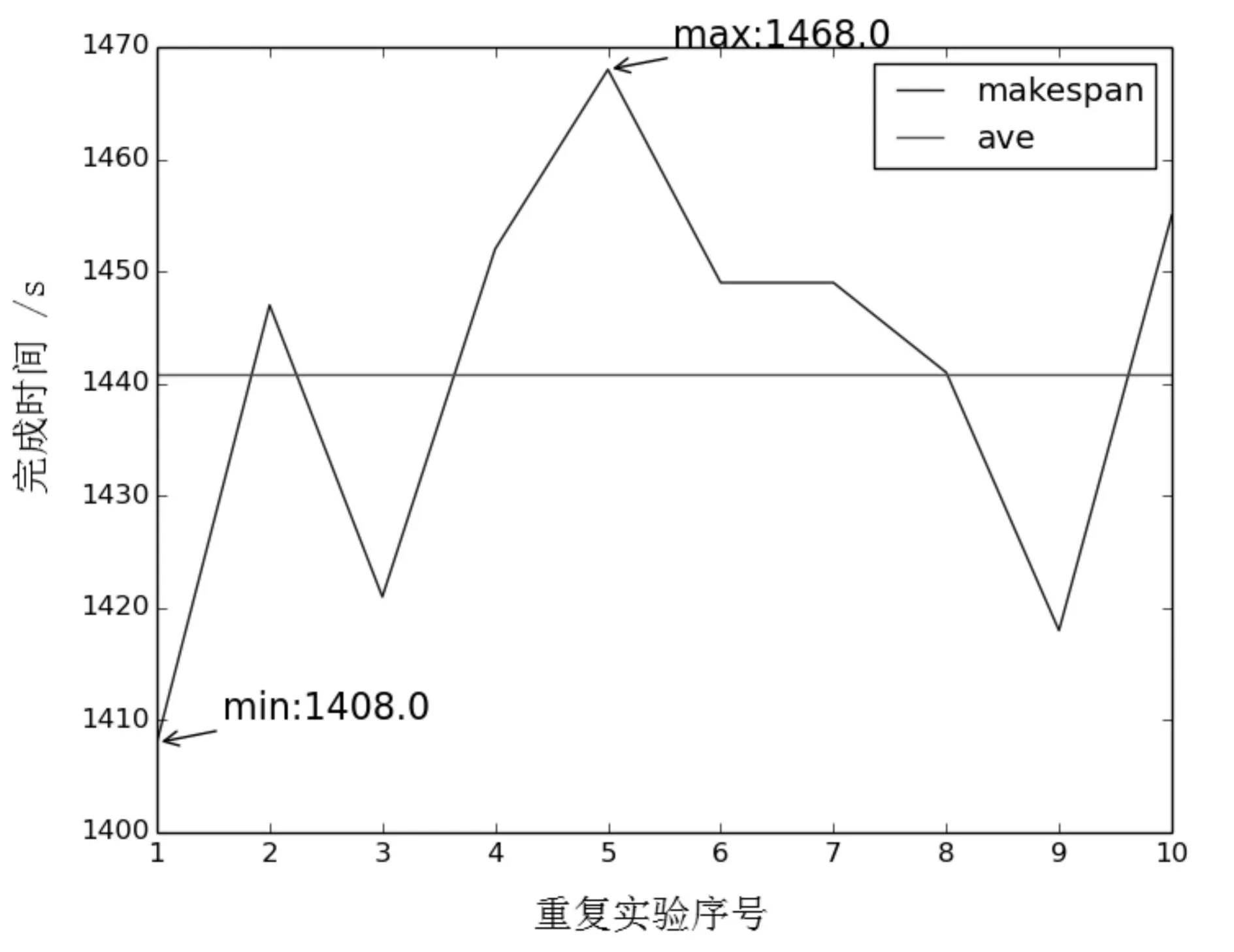
在人们生产生活的诸多领域都存在着调度问题，例如工厂如何分配工件在合适的机器上执行；此外，随着互联网的发展，云计算已经成为一大热点，如何对云环境下的资源进行调度，本质上也是此类问题.优良的调度策略能够极大地提高生产效率.

本文对无联系并行机器调度问题(UPMSP)[1]进行研究.问题可以描述如下：有N个任务在时间点0处开始，有M台机器可供这些任务运行，最终的调度目标是使这些任务总的完成时间(makespan)最小，其中M

在M不大的情况下可以在多项式时间内找到最优解；反之，是一个NP-hard问题，采用启发式的算法可以在合理的时间内找到一个近似解[2,3].

一些研究者开发了确定性算法来解决UPMSP问题.在文[4]和[5]中，Liaw和Lancia开发了分支定界法来找出最优解.

另外一些研究者考虑采用启发式的方法来解决此问题.在文[6]中，作者考虑了增加负载均衡这一条件，并采用蚁群算法求调度策略的解.Arnaout采用蚁群算法来解决有安装时间限制和有任务依赖下的UPMSP问题，经过实验表明此算法性能更好[7].最近，Arnaout又提出了一个两阶段蚁群算法来最小化总任务的完成时间[8]，该算法在第一阶段通过蚁群算法找出放置在机器上的合适的任务，第二阶段在机器上对这些任务进行合适的调度使得总完成时间最少.

本文的关注点在于利用蚁群算法解决机器数目与任务数目都较大情况下的UPMSP问题.通过仿真实验说明蚁群算法可以解决UPMSP问题.

1基于UPMSP的ACO算法

1.1UPMSP模型

ti(i=1,2,3，…,n)表示第i个任务，T={t1,t2,…,tn}表示这n个任务的集合；mj(j=1，2，3,…,m-1,m)表示第j台机器，M={m1,…,mm}表示m台机器的集合.ti放置在mj机器上执行，其运行时间记为pij，N个任务运行在M台机器上的运行时间用pij组成的矩阵P表示；kij代表指标矩阵中的某一元素，若为1表示第i个任务分配在第j台机器上，否则为0，这标明了在P矩阵中选出哪些元素.模型如下：

(1)

Subjectto:

(2)

kij∈{0,1},i=1,2,…,n;j=1,2,…,m.

(3)

限制如下：(1)n个任务之间没有依赖，即任意一个任务可以在任意时刻执行；(2)任一任务不能被抢占；(3)一个任务在任一机器上执行完毕就不再参与.

1.2算法流程及说明

(1) 总体流程.算法总体流程见表1.

表1　ACO 算法

算法首先对如下数据进行初始化：信息素矩阵、任务序列、迭代次数(算法1第2句).之后不断迭代直至迭代次数达到最大值(算法1第3句)，在每轮迭代中每个蚂蚁会爬一条路径，这条路径经过的点就是解(算法1第4句)，之后对蚂蚁爬过的信息素进行更新(算法1第5句).

(2) 初始化.信息素矩阵的所有元素初始化为1，同时生成一个任务序列.τij表示分配任务i到机器j上的信息素.信息素τij组成信息素矩阵T.

在构建解的过程中，蚂蚁需要重复一个基本的决策过程[9]：选择哪个机器来完成这项任务，其中任务的次序不进行学习，即预先给定一个任务序列，每个蚂蚁都按这个序列的次序行进，在爬取的过程中只学习任务与机器之间的信息素.信息素与任务和机器的组合有关.

(3) 任务选择. 选择执行指定任务的机器的概率如下：

(4)

(4) 信息素的更新. 如果此轮迭代某个蚂蚁得到的最优解优于全局最优解，那么对信息素进行如下更新：

(5)

1.3实验设计

机器硬件配置如下：CPU为Intel core i5 4590，内存为16GB.本仿真实验在Python2.7上实现.

(1) 任务序列. 本实验的任务序列是从小到大的一个有序序列(1,2,3，…,n).

(2) 机器数和任务数的组合. 在真实环境中为了使机器得到充分利用，任务数需要大于机器数.基于文献[8]，在实验中设置任务数和机器数的比值为N/M≥15，具体设置如下：机器数目为2与任务数集合(40,60,80,100,120)中任一元素的组合；机器数目4与集合(60,80,100,120)中任一元素的组合；机器数目6与集合(100,120)任一元素的组合；机器数目8与任务数120的组合.由此，共得到12个机器数目和任务数目的组合.

(3) 任务运行时间矩阵. 在此采用文[8]的做法，设置了运行时间满足均匀分布：U～(50,100).为说明问题简单起见，单位设置为秒.

(4) 参数. 经过多次试验，ρ和Φ分别设置为0.01和0.3算法可以达到较好的性能.

(5) 迭代次数. 在处理任务数目与机器数目比值相对较大的情况下，可能在迭代终止时蚁群算法并没有收敛，因此迭代次数需要相应增加.经过试验，迭代次数设置为3种：300，500，1000.在300的情况下，算法可以较快结束；在1000的情况下算法基本可以收敛；500次迭代是为了取上述两种的中间情况.

(6) 蚂蚁个数. 通过不同的蚂蚁数目，观察其对解的影响.本实验中个数设置为8和12.

(7) 重复次数. 为了比较在同一条件下算法的性能，进行重复实验10次.

故在10次重复实验、3种迭代参数、2种蚂蚁数量、12种组合的情况，共计进行了720(10×3×2×12)次实验.

2实验结果及分析

实验结果及统计数据见图1和表2.

图1是在机器数为2和任务数为40的情况下蚁群算法的收敛图.minMakespan和maxMakespan分别代表每轮迭代中的最小完成时间和最大完成时间.由此可知，在迭代次数接近150处最小完成时间开始收敛，在180左右，最大完成时间开始收敛.其它组合情况类似.

图1　收敛情况Fig.1　Convegence situation

由表2可以看出，相邻组试验中，随着蚂蚁数目的增加，有的解变得更好，而有的则不然，所以不能看出蚂蚁数量对于解的好坏的决定性因素.原因有两个：一是每只蚂蚁只搜索了一条路径，蚂蚁数量越多得出的解就越精确，但是若很多蚂蚁都没有找到一条比以前更优解，那么解不见得会更好；二是蚁群算法过早收敛陷入了局部解，这样算法不能找到更优解.针对陷入局部解的解决方法有两个：(1)多次试验，设置合适的挥发因子等其他参数，但是此种方法或会导致算法只能适用在特定问题的特定数据集上，算法的通用性较差；(2)增加局部搜索算法，这样每个蚂蚁得到一个最优解之后都会继续进行搜索，此方法的问题是不仅增加了算法的复杂度，而且也需要对特定问题进行局部搜索的算法设计.针对上述问题及解决方案，在后续的研究中会作进一步探索.

表2　近似解统计数据

图2　重复实验的结果Fig.2　The results of repeated experiments

图2是机器数为2、任务数为40、蚂蚁数为8的情况下10次重复试验的解.10次实验中最小值和最大值的差异并不大，比如在(2,120,12)行中，最小值为4001，最大值为4088，差值仅为4001的2.1%.所以在实际生产环境下可以不进行多次重复实验.同理在表1其他行也可以看出类似的情况.

在实验中，随着迭代次数的增加，算法运行时间也会增加，所以基于此可以减少算法的运行时间：本次实验中迭代次数是固定的，以后的实验中可以对此进行改进，一旦算法已经收敛，就不需要运行至已设的最大迭代次数.

综上说明无联系任务的调度策略可以通过蚁群算法得到近似解.

3扩展实验

上文中，每个蚂蚁都是从第一个任务按序爬至最后一个任务，并没有对任务之间的信息素进行更新，而只更新了任务在机器中的信息素，下面通过实验探求不同的任务次序对解的影响在本文的试验中，如果任务有40个，任务次序的排列有40!种，对全部排列进行实验是不可能的.故实验设计为两组，在任务数和机器数的组合为40和2的情况下随机选取了30000个不同的任务次序进行实验；对于80和4的情况下则选取了3000个，统计得到解的分布.对上述算法1的初始化部分进行修改，每次实验生成一个不同于之前的排列.

对3000和30000个不同任务次序进行实验，表3的结果表明：最小值与均值的差异并不大，但最大值与均值相差较大，说明较多的解分布在均值附近，较差的解出现的次数较少.

表3　统计数据

如图3所示，任务数40和机器数2情况下，大多数解密集分布在1400左右，图像出现了某些毛刺，说明这些解较差.从总体上看，没有出现解的某种分布倾向，图4类似.在UPMSP问题中，因为任务与任务间并没有先后顺序的约束，所以并不需要学习任务之间的信息素.综上得出结论，任务次序对UPMSP问题解的影响可以忽略.

图3　30000次试验下解的分布Fig.3　Distribution of solution in the 30000 case

图4　3000次试验下解的分布Fig.4　Distribution of solution in the 3000 case

4性能分析

引入文[10]中的时间性能评价指标，同时为了适应本研究的目的，对其做了些许修改，如下：

(6)

Ia为算法满足终止条件时平均的迭代次数，Imax为给定的最大迭代次数.显然，E值越小，算法的收敛速度越快.该指标直接衡量了算法搜索可行解的快慢程度.

为简单起见，同时能说明问题，实验设置的最大迭代次数Imax为1000，在10次重复实验、1种迭代参数、2种蚂蚁数量、12种组合的情况下，共计进行了240(10×1×2×12)次实验，实验数据见表4.

表4　E的统计数据

在实验中，有24组条件，每组重复实验10次.在24组条件中，有5组条件的10次重复实验有9次收敛，其他19组条件下的10次重复实验都收敛.

从表4可以看出，有的条件下，蚂蚁数目变多，收敛会加快；而有的则不然，蚂蚁数量对收敛速度的影响需要作进一步研究.另外，在机器数不变的情况下，任务数变多，收敛所需的时间会变多，如在机器数为2的情况下，任务数增加，E值的趋势是变大的，这是因为搜索空间变大，故搜索的时间也相应增多.在任务数不变、机器数目变多的情况下，并没有表现出明显规律，如任务120、蚂蚁12的情况下，E值分别为21.00%、22.47%、18.34%和17.72%，对其可能存在的规律还需要进一步的探索.

本性能实验仅仅是通过仿真的方法来探索不同条件下此问题蚁群算法的收敛时间，因此在以后的工作中，还需要对其收敛性进行理论研究.

5结论

合理的资源调度能有效地增加生产效率，因此对调度策略的研究具有重大价值.本文仿真实验结果表明：可以通过蚁群算法得到UPMSP近似解；基于任务次序的研究说明，任务次序对近似解在统计意义上没有显著影响；关于性能分析的实验说明随着任务数目的增加，此算法需要更长的时间才能收敛.

参考文献

[1]唐国春. 现代排序论[M]. 上海: 上海科学普及出版社, 2003:5-14.

[2]Garey M R, Johnson D S. Computers and intractability: a guide to the theory of NP-completeness[M]. San Francisco: Freeman, 1979: 236-243.

[3]Karp R M. Reducibility among combinatorial problems[M]. New York: Springer US, 1972: 85-103.

[4]Liaw C F, Lin Y K, Cheng C Y, et al. Scheduling unrelated parallel machines to minimize total weighted tardiness[J]. Computers & Operations Research, 2003, 30(12): 1777-1789.

[5]Lancia G. Scheduling jobs with release dates and tails on two unrelated parallel machines to minimize the makespan[J]. European Journal of Operational Research, 2000, 120(2): 277-288.

[6]张焕青, 张学平, 王海涛, 等. 基于负载均衡蚁群优化算法的云计算任务调度[J]. 微电子学与计算机, 2015, 5: 7.

[7]Arnaout J P, Rabadi G, Musa R. A two-stage ant colony optimization algorithm to minimize the makespan on unrelated parallel machines with sequence-dependent setup times[J]. Journal of Intelligent Manufacturing, 2010, 21(6): 693-701.

[8]Arnaout J P, Musa R, Rabadi G. A two-stage ant colony optimization algorithm to minimize the makespan on unrelated parallel machines—part II: enhancements and experimentations[J]. Journal of Intelligent Manufacturing, 2014, 25(1): 43-53.

[9]Dorigo M, Birattari M. Ant colony optimization[M]. New York: Springer US, 2010: 36-39.

[10]谭明交, 张宏梅, 吕艳秋. 群体智能算法及其性能评价指标研究[J]. 计算机与数字工程, 2008, 36(8): 10-12.

中图分类号TP301.6

文献标识码A

文章编号1672-4321(2016)01-0127-05

基金项目国家民委教改基金资助项目(15013)；中南民族大学研究生创新基金资助项目(2016sycxjj199)

作者简介王文涛(1967-)，男，副教授，博士，研究方向：计算机网络与控制，E-mail：wangwt@mail.scuec.edu.cn

收稿日期2016-01-07