慢养数学：小学生数学求异思维发展之我见

王海静

摘 要：慢养不是放慢生长的步伐，而是拓宽学生的生长路径，遵循学生成长的规律，允许学生在成长的过程中，自由生长，而不是按固定的模式，改变其生长速度或季节。学生数学求异思维的形成过程也需要这样的一个慢养的过程，不能一蹴而就，要让学生慢慢地经历求异思维的形成过程，所以在数学教学中，教师更应该将知识植根于生活，致力于学生的数学求异思维养成过程教育，促进学生形成高品质的数学思维。

关键词：慢养；数学思维；求异

慢养不是放慢生长的步伐，而是遵循学生成长的规律，拓宽学生的思维宽度和广度，允许学生在思维形成的过程中，像野花一样，经历风霜雨露，自由生长，而不是放在温室里，按固定的模式，改变其生长速度或季节，只有慢养中成长起来的孩子才能更加坚韧。

一、慢养，让数学求异思维经历生长过程

（一） 慢养修其身

学生的思维发展应遵循其规律。没有思维的生长过程，甚至不需要思考，只需记住答案即可，这种现象在教学中比比皆是。于是学生厌学，教师厌教只能以新的方式延续。

1. “慢”，使数学求异思维循序渐进生长

儿童思维生长的过程就是思维在原有的基础上循序渐进不断提升的过程，循序渐进是儿童思维发展的客观规律。儿童时期是人的一生中思维最宽松、最独立没束缚的阶段，他们的思维可谓是天马行空，而这一阶段正好也是培养“求异”思维的最佳时期。儿童毕竟是稚嫩的，思维也一样，所以培育“求异”思维必须讲究循序渐进，即由深入浅，由简到繁，从易到难。在课堂教学中，要运用多种教学手段，让学生动口、动手、动脑，努力拓宽思路，调动他们积极参与，促进学生的“求异”思维，切实让素质教育走进教学课堂。

2. “慢”，让数学求异思维生长土壤更广阔

学生思维生长的土壤决定其质量，教师应致力于为学生提供更广阔的空间，促进学生求异思维向更优化的方向发展。在教学过程中，不能只重视结果，要针对教学的重难点，精心设计有层次、有坡度，要求明确、题型多变的练习题，让学生经历不断探索的过程，从而让数学求异思维渐入佳境。

（二）慢养求其性

1. “慢”，凸显数学求异思维的独创性

思维独创性指敢于超越传统习惯的束缚，摆脱原有知识范围的羁绊和思维定式禁锢，善于把头脑中已有的知识信息重新组合，产生具有进步意义的新设想和新发现。求异探索是一种富有创造性的辨异思维，教学中教师应着力引导学生敢于突破陈规，提出大胆设想和独特的见解，鼓励学生标新立异，另辟蹊径，探寻到具有创新意识的妙法，达到培养思维独创性的目的。独创性意义在于主动地、独创地发现新问题、提出新见解、解决新问题。使学生在思维方式上摆脱“框题型、对套路”的僵化模式，从而有效激发学生创造性火花。

在课堂教学中，我们经常会发现学生的独到的思维。如：教师提问：有没有最大的正整数、最小的负整数？为什么？一个学生回答：没有，因为再大的正整数，加1还有更大的，再小的负整数，减1还有更小的。显然，学生的回答是非常精彩的，而教师不置可否，继续让其他学生回答。为什么一个从不吝啬表扬的教师，面对如此出色的回答却无动于衷呢？面对这样的现象，教师缺乏对学生思维独到性的感知，更缺乏对其鼓励。

2.“慢”，追求数学求异思维流畅性

求异思维的流畅性是指发散的量，其发散的项目愈多，说明思维的流畅性愈好，流畅性因素主要依赖记忆中贮存的信息量。由此可见，学生求异思维的流畅性也是我们对思维培养的又一追求。

二、慢养，另辟数学求异思维的蹊径

（一）打破思维规范，引导“慢思考”

不同学生有着不同的思维方式，教学中应该极为关注学生在数学学习活动时的个性差异，允许学生思维方式的多样化和思维水平的不同层次。全美最佳教师罗恩·克拉克来华做教学交流，其展示课中有这样一个环节：

师（随意在白板上画了一个正六边形）：计算一个正六边形的面积需要几个数据？

生1：需要三个数据。上台画出示意图：把正六边形对半平均分成两个梯形，支出需要的三个数据分别是梯形的上底、下底和高。

生2：只需要两个数据，把正六边形平均分成6个三角形，只需要知道三角形的底和高。

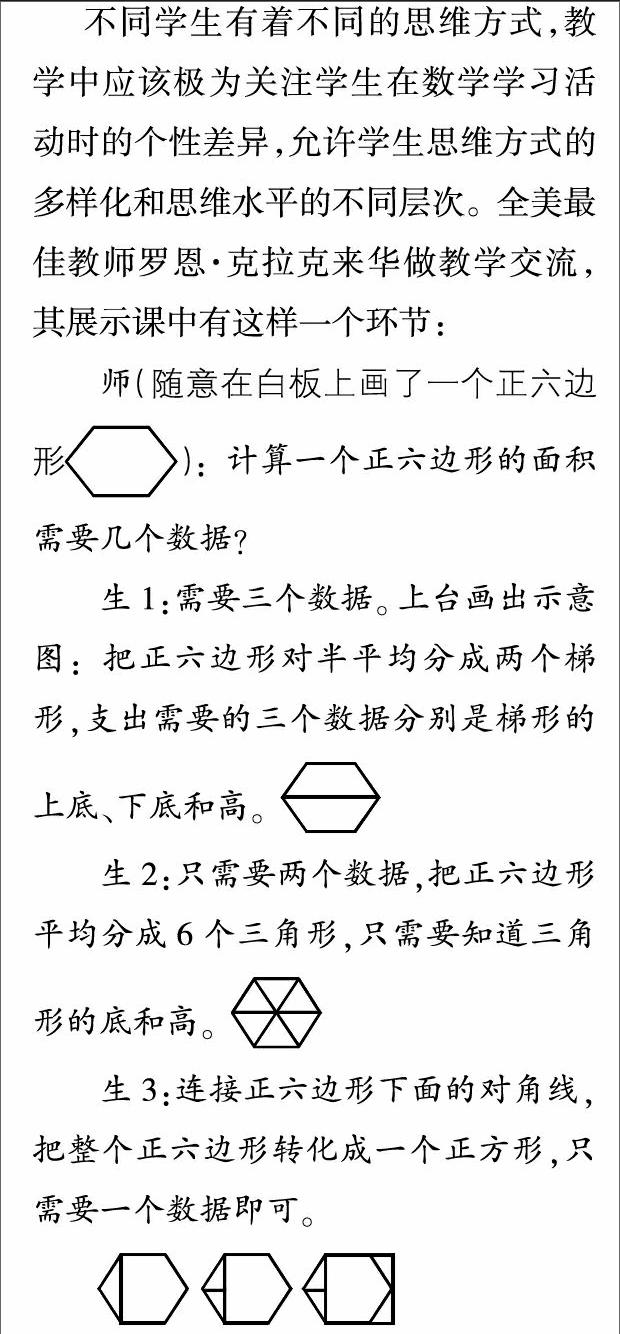
生3：连接正六边形下面的对角线，把整个正六边形转化成一个正方形，只需要一个数据即可。

以上的教学环节没有具体的数据，也不需要学生的计算，打破了学生看题目的思维定式。罗恩·克拉克说：“与其给条件让学生去计算面积，不如让学生自己思考需要怎样的条件才能计算出面积，我们在课堂上，应经常出一些这样的练习，用不一样的思维来锻炼学生。”

（二）亲自参与，鼓励“慢发现”

数学教育家波利亚说过：“学习任何知识的最佳途径，都是由自己去发现、探索、研究，因为这样理解更深刻，也最容易掌握其中的内在规律，性质和联系。”小学数学教学中，教师必须牢记“组织者、引导者、合作者”的职责，提供学习活动的条件，努力创设有利于学生参与的教学环境，帮助他们在“动手实践、自主探索、合作交流”中最充分地参与学习活动，真正理解和掌握基本的数学知识与技能，数学思想与方法，获得广泛的数学活动经验的同时获得成功的积极情感体验。

教学苏教版二下《角的认识》时，教师要让学生自己根据角的特征制作一个角。因为认识角，对于二年级学生来说比较抽象，学生接受起来也比较困难，因此为了帮助学生更好地认识角，教师可以让学生制作一个角，在制作的过程中，进一步加深对角的特征的认识。整个教学过程将观察、操作、演示、猜测、验证、讨论等方法有效地贯穿于整个教学之中，引导学生在感性认识的基础上加以抽象概括，尊重了学生的年龄特点和认知规律。在“摸角”和到生活中“找角”以及后来的“画角”，给了学生实践操作的实践和空间，让他们学会展示自己和有机会展示自己，在实践中探索新知，增强他们主动探究的意识，使学生获得了成功的喜悦。

（三） 关注数学素养，引领“慢成长”

数学素养是指学生在从事数学学习与应用活动的过程中，通过主体自身的不断认识和实践的影响下，使数学文化知识和数学能力在主体发展中内化，逐渐形成和发展起来的“数学化”思维意识与“数学化”地观察世界、处理和解决问题的能力。

1. 课内交流，实现思维多变

新课改理念下的数学课堂有了很大的变化，课堂开放了，数学课堂变成生成的课堂。课上交流能引导学生逐步形成知识，在交流的过程中，学生学会选择有效的数学信息，在交流中引发学生深入的思考。

学生从不同角度思考问题，这是求异思维发展之根。有这样一道数学题：小明和小华投飞镖，均投了5次，小明的成绩是5环、6环、7环、8环、9环；小华的成绩是10环、4环、7环、7环、7环，请你说一说，谁表现得更好一些。学生在分析的时候，有的从平均数的角度思考，两人的成绩一样好；也有的从发挥的情况思考，小华第一次就投中10环，他有冲击冠军的实力；有的认为小明表现好一些，因为他的成绩越来越好；还有的运用众数的知识来分析，认为小华的成绩相对稳定，所以表现更好一些。在不断的交流反思中，学生能从不同角度思考问题，实现数学求异思维的生长，彻底改变生硬的知识教学的面貌。

2. 课外使用，实现思维高层次成长

数学学习的最终目的是用数学解决问题。在日常学习和生活过程中，实现学生主动将生活与数学联系。例如：算24，本是一个游戏，即任意四个数，利用加减乘除，算出24。这也是在小学低年级学生就接触到的开放题，针对这样的开放题，先要学生用逆向的思维方式和求异的思维方法，在大脑中进行多次的计算并验证，才能获得结果。学生在此过程中，不断变换思考途径，思维得到高层次的成长。

慢养数学，其目的是拓宽学生数学学习的思维，使学生的思维不受课本知识的束缚和局限，允许学生思考问题时标新立异，它是一个慢养的过程。在这个过程中，教师要发挥职业智慧，为学生得到良好的数学教育，形成高品质的数学素养提供阳光雨露，这才是数学教育的应然追求。