摆正位置,科学引领,激发探究的实效
2016-04-22倪燕琴
倪燕琴
摘 要:探究性学习是《数学课程标准》提出的学生的重要学习方式之一,这样的学习方式有利于激发学生的主观能动性,调动学生综合利用各种学习资源的能力,拓展学生的实践、推理、分析和交流的能力。所以在小学数学的课堂教学中,我们首先是要认可这样的教学方式,不要因为一时的得失而轻易否定它,其次是要创造条件让学生进行深层次的探究,促进学生因疑而学,学而有所悟。
关键词:小学数学;科学引领;有效探究
小学数学教学中我们不仅应当关注学生探究知识的程度,而且要关注学生的探究过程和探究方式,指导他们更有效地展开自主探究。这样的学习一定是有意义的,有内在增长力的,是值得我们大力推广的:
一、勇于尝试,摆正探究性学习的位置
有些教师对学生的探究能力是抱有怀疑态度的,因而在他们的教学中,学生的探究是“戴着镣铐的”,他们不敢放手让学生去面对有一定内涵的问题,只有在“可控范围内”才会让学生象征性地展开“探究”,然后心满意足地收获学生的探究成果。久而久之,学生对这样的“伪探究”会失去兴趣,探究就越来越流于形式了。其实有这样的怀疑属于正常,教师对自己一直坚持的教学方式比较自信,认为这样的言传身教能够有更好的教学效果,这本是无可厚非的态度,但是认真思考一下,如果永远不敢放手,那么学生只能一直学习在教师的指挥棒下,他们的自主性会削弱,创新思维会停滞,甚至研究问题的渴望都会得到消磨,这样的学习绝对不利于学生的终身发展,所以从这个角度来说,我们应当真正解放学生,放手让他们去探究。对于探究中出现的问题我们应当倍加珍惜,因为很多经验都将来源于这些问题。
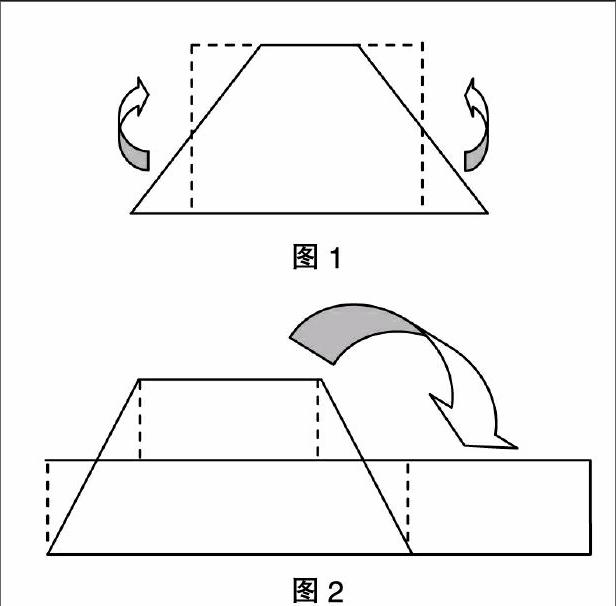
例如“梯形的面积”教学,在出示学习内容之后,笔者请学生展开自我探究,然后组织交流。交流中发现了几种不一样的方法:一是传承三角形面积计算的方法,用两个一模一样的梯形拼成一个平行四边形,这样由平行四边形的面积等于梯形的上底加下底的和乘梯形的高推导出梯形的面积公式。二是根据教材中提供的“以盈补虚”的方法,在方格图上将梯形转化为长方形来求,并且学生的转化方式还不同(见图1和图2)。面对这样的不同方法,学生展开了激烈的交流,他们发现第一种方法与三角形的转化方式相似,转化为一个高和原来相等的长方形,而长方形的两条长的和等于梯形的上下底之和,因而可以推算出长方形的面积等于梯形的上底加下底的和除以2再乘高。而第二种方法就有些另辟蹊径了,它是沿着梯形的高的一半截开,将上面的两个三角形旋转并拼凑到下面,形成一个长方形,然后将上面剩下的长方形平移下来,转化为一个长等于的梯形的上下底之和,宽等于梯形高的一半的长方形。这样的两种方法虽然不同,但是都成功地将梯形转化成长方形,从而推导出梯形的面积计算公式。
如果不是充分放手,让学生根据自己的想象去尝试,去探究,那么学生对梯形面积的学习就只能停留在方法一上,这是一种简单的模仿,现在这样的学习是多层次的,不同的方法让学生从不同的途径得到了相同的计算方法,学生对梯形的面积公式是认可的,并且在推敲方法二和方法三的过程中,学生对转化的方法有了更深的了解,对“以盈补虚”的方法也做出了尝试,这有利于他们形成基本的数学思想。这个案例展示了学生的“不同”,体现出他们的创造力,在这样的铁证面前,我们有理由相信学生能在自我探究中实现数学能力的跨越,累积丰富的数学学习经验,从而为他们的可持续学习打下坚实的基础,我们更加坚信了探究性学习的力量,从而有了敢于放手和勇于放手的底气。
二、不断探索,提升探究性学习的质量
任何探究不会凭空而来,一定有其因,有其果。在学生的自主探索中,我们要努力为学生营造一个良好的氛围和环境,让他们的探究有良好的开端、丰盈的过程和美好的结果,这样学生在探究性学习的道路上才会越走越宽广。
1. 激发探究的欲望必不可少
培养学生的探究能力可以从激发学生的探究欲望入手,当学生面对感兴趣的数学问题,急于探求其中的知识时,他们会产生积极的探究欲望,从而驱动他们的探究向深层次,向多元化发展,这样的兴趣可能来自于一个巧妙的情境,或者来源于一个现实的问题,让学生在不同的情绪中迸发出能量。
例如“探索能被2、3、5整除的数的特征”的教学中,笔者先与学生做了一个比赛,师生各自写出10个10000以内的数,然后教师与学生来共同判断这些数哪些是2的倍数,哪些是3的倍数,哪些是5的倍数(学生在小组内分工合作,以小组为单位参赛),先判断完并全部正确的一方获胜。结果笔者以完美的表现征服了学生,在他们表示惊讶、赞叹、不服等情绪的时候,一种无声的欲望自然涌上学生心头:老师是怎么做到的?有了这样的想法,学生的探究欲油然而生。
2. 思辨的习惯是探究的关键
探究是基于已有知识经验上的对未知区域展开研究的活动,在这样的活动中,除了行动上的参与之外,学生的思维也要充分活跃,要让他们养成思辨的习惯,这样的思考会让学生的探究更全面、更成熟,更有质量。
例如“认识倒数”的学习,在学生自学相关内容之后,笔者引导学生将自己的收获和疑问整理下来,然后在小组内交流,共同解决自己认为有价值的问题。之后的全班交流中学生展示了很多挖掘得比较深入的问题,比如“为什么0没有倒数”、“负数有没有倒数”、“怎样来求小数的倒数比较简单”等等问题,在这些问题被一个一个解决的时候,学生对倒数的认识也越来越清晰,对相关的数学概念的理解也越来越深入。
当学生习惯于疑问和反问的时候,说明他们掌握了探索的方法,有了建立在自己认知基础上的向上突破的动力,数学探究就应当在这样浓郁的充满思辨的氛围中展开,让探究因为思索而延续得更久远。
3. 交流是探索的必备工序
俗话说“它山之石可以攻玉”,学生的自主探究虽然是以个人探究为主,但是如果探究总是“单兵作战”,那么学生难免会陷入困难。所以在探究中我们要引导学生加强交流,在相互交流中得到启发,在相互交流中促进认识深化,在相互交流中实现探究的精益求精。
例如在“商不变的规律”的教学中,在总结商不变的规律时,有学生提出“被除数和除数同时扩大(或者缩小)相同的倍数”这一句描述中同时和相同都是比较关键的,得到了大家的认同。在此基础上,有学生提出是不是可以分别来研究一下被除数和除数两个量其中的一个变化另一个不变时商的变化规律,这样的提议激发了大家的兴趣,于是学生立即设想了研究方案,从一组被除数保持不变的式子和一组除数保持不变的式子入手来展开探究,并将自己的发现与其余小组成员交流。在展示的时候,学生成功地发现在除数不变的基础上商的变化与被除数保持一致,而被除数不变的时候商的变化正好与除数的变化相反的规律。这样的发现比商不变的规律更有深度,也能推动学生更深刻地理解除法算式的意义。
当然除了这些因素之外,还有许多关乎探究成败的细节,比如教师发挥的作用、探究中的生成情况的处理等等,我们应当在实践中多关注这些问题,不断总结,不断提升,推动学生的数学探究的质量不断攀升。
三、关注过程,展现探究性学习的意义
对于学生的探究性学习,我们不但要关注他们有了哪些发现,对于学习内容的领悟到达了怎样的层次,同时要关注学生的探究过程,给予他们科学的评价和智慧的引领。当我们将不同学生的不同做法、不同想法和不同的学习态度展现出来的时候,学生从中收获的就不仅仅是知识本身,更有学习方法上的促进。
例如在“钉子板上的多边形”的教学中,在引导学生猜测钉子板上的几何图形的面积与钉子数(有的认为与内部钉子数有关,有的认为与边上的钉子数有关)有关之后,笔者就让学生自己来设计方案并展开研究。一段时间之后,有的学生有了自己的发现,也有很多学生没有进展,于是笔者请一位学生来介绍一下自己的成功经验。学生带给了大家这样一段介绍:这一课研究的是几何图形的面积与钉子板上的钉子之间有没有关系,通过观察我们可以发现几何图形的边上有钉子,有的内部也有钉子,那么图形的面积到底和哪里的钉子数有关呢?我想先要解决这个问题然后才能展开研究,于是我在钉子板上围了几个不同的图,大家看看,同样是内部有一个钉子的正方形和三角形,面积明显不同,那么导致面积不同的原因就在于图形边上的钉子数不同,至于形状相同,内部的钉子数不同的相同图形,我们甚至不要计算就可以判断出图形的面积与内部的钉子数有关。有了这些思考,我先将内部的钉子数固定,再画出不同几何图形来研究面积与边上的钉子数之间的关系,然后再改变内部的钉子数来继续研究。
这样的一段描述将学生的做法和支撑这样研究的理由阐述得淋漓尽致,笔者想那些找不到突破口的学生在经历这样的介绍后会有不少的启发,在我们肯定这些成功者的时候,学生一定会以他们为榜样,模仿他们的做法,体会他们这样做的原因,有了这样的微观定格,再遇到相似问题的时候,大家都能有探究的切入点,有个性化的设计,这就为学生更有效地展开探究性学习提供了帮助。
总之,探究性学习是经实践证明的行之有效的学习方式,我们的教学中要充分发挥探究的魔力,让学生的数学学习因为探究而深刻,因为探究而灵动,因为探究而多样化。
