关于三角剖分的简单分析

2016-04-21张尧马聪刘翔

地球 2016年6期

关键词：剖分等值线原始数据

■张尧马聪刘翔

（辽宁省地质勘查院辽宁大连116100）

关于三角剖分的简单分析

■张尧马聪刘翔

（辽宁省地质勘查院辽宁大连116100）

在物探的工作过程中，为了绘制等值线图，必须对实测的离散数据进行网格化。由于受到了客观要求，我们工作中绘制的等值线图所使用的网格化方法均为三角形剖分法。在长期使用三角剖分的绘图工作过程中遇到了种种现象，如：所绘等值线与手绘等值线相似性较大；所绘等值线圆滑程度不理想；所绘等值线容易出现顺线的趋势等。现本人试图对以上现象进行简单分析，并将一些感想写下来。

三角剖分网格化物探

本人所在二级单位主要使用mapgis及GeoIPAS作为绘图软件绘制物探的等值线图。以上两种软件分别提供了数种不同的网格化方法，为了与三角剖分做比较，现列举几种主要的加以描述：

克里格方法是根据相邻变量的值,利用变差函数所揭示的区域化变量的内在联系来估计空间变量数值。该方法总是尽可能地去描述原数据所隐含的趋势特征,以区域化变量理论为基础,以变差函数为主要工具,在保证研究对象的估计值满足无偏性条件和最小方差条件的前提下求得估计值[1]。

最小曲率法采用迭代的方法逐次求取网格节点数据,其插值面类似一个薄的、线性—弹性形变板,该“板”经过所有的数据点,且每个数据点具有最小曲率。在尽可能体现原数据的同时,最小曲率法产生尽可能的光滑曲面,绘制的图件比较美观。

径向基函数法,是多个数据插值方法组合的一种多形式网格化方法。其基函数是由单个变量的函数构成的,通过选择不同的基本函数来定义不同的加权方法,进行不同方式的网格化。所有径向基函数插值法都是准确的插值器,它们都能尽量适应数据。

三角形剖分法是一种严格的插值方法,使用最佳的Delaunay三角形,通过直线连接各数据点形成一系列三角形,并且所有的三角形互不相交,每个三角形内的网格节点值由该三角平面决定。由于采用所有的数据点去构造三角形,因而原数据能得到很好的体现,给定三角形内的全部节点都要受到该三角形的表面限制。最佳三角形的选取原则为：三角形三个内角尽量都是锐角，三条边长度尽量相等，最小角最大化。因此最适合三角剖分的离散数据排列方式如图1所示，即连成的三角形均是等边三角形。

各种网格化方法原理及切入点虽然各异，但最终目的相同，都是为了做成连续的曲面，尽量真实的反应实际的地球物理场状况。各种网格化方法决定待插值结果的因素我认为有以下几点（待补充）

（1）插值所使用的数学模型。这是决定不同网格化方法的直接因素，采用不同的插值方法对最终结果的精度及曲线的圆滑程度等都有直接影响。为了尽量达到更高的精度，一些网格化方法使用较为繁琐而复杂的函数，所绘制等值线圆滑而细腻。相对而言，三角剖分采用的差值方法相当于两个线性插值的叠带（如果待插点位于三角形边上则插值方法仅为线性插值），函数非常简单，因此所绘制的等值线不够圆滑，较为生硬。Mapgis在以TIN成图的过程中可以对曲线做一定程度的圆滑处理，这是在网格已经生成之后所做的，应属抛开插值单独做圆滑处理，是为了尽量扼制局部的曲率突变，而非考虑实际地球物理场的规律，处理程度若较大会使精度大幅下降，有时甚至出现等值线交叉的情形。

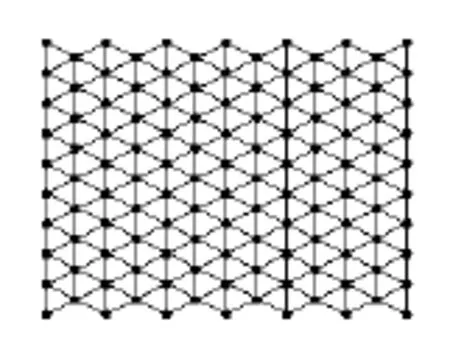
图1 三角剖分最理想的网度

（2）待插值与参与插值原始数据的距离。以此为切入点的网格化方法称为距离法，由此将过程细化复杂化而衍生出一系列方法。各种网格化方法均或多或少受距离影响，即待插点越接近原始数据，则其结果越受之控制。三角剖分显然也受距离影响，如图2所示：A、B、C为围成三角形的三个原始数据，D点为待插点。若其余条件未变而使C点处于如图2-2位置，D点与C点间的距离减少，相较图2-1,D点的结果更受C点控制。

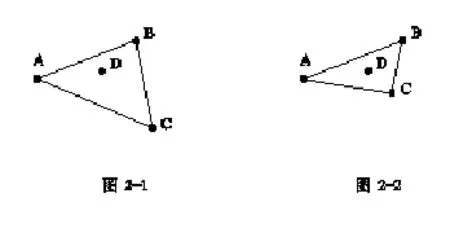
图2

（3）参与每一待插点的插值过程的原始数据范围。参与单一待插点差值的原始数据范围越小，越能突出局部细节，范围越大则越突出区域特征而扼制局部细节。范围过大则生成曲面过于平缓、细节大量流失，范围过小则不能连成完整曲面。一些网格化方法可以自由选择圈定原始数据范围，可以使结果细节完善或反映区域信息，与之相比三角剖分网格不能脱离最佳三角形，已进行最优选而得到唯一结果（除非最佳三角形不只一种可能性），参与单点插值的原始数据只能为2-3个，所绘等值线为唯一结果。

综上所述我认为三角剖分相较于其他网格化方法是一种简单、直接、结果唯一的插值方法，当精度要求不高时算是一种比较好的网格化方法。现试图对前文所述现象加以解释：

所绘等值线与手绘等值线相似性较大，我认为造成这种现象的原因在于两者均有以下特征：1.尊重原始数据。三角剖分由于采用线性插值，因此不会产生高于原始数据最高值及低于原始数据最低值的点，曲面极大值与极小值与原始数据的位置与数值均保持完全一致；2.原始数据点与点之间的差值分配按照线性分配；3.圆滑方式相似。单凭人力在有限的原始数据中不能发现最能反映客观地球物理场的规律，因此手绘的圆滑处理出于一定程度上的合理以及美观的目的，与前文三角剖分的圆滑方式类似。

所绘等值线圆滑程度不理想，前文已经提到是由于三角剖分使用线性函数插值，不再阐述。

所绘等值线容易出现顺线的趋势，这是由于我们的物探工作所采用的网度都是线距大于点距，形成的最佳三角形最短边是第二短边的1/2.5或1/5，并不十分理想。如图3-1所示，A、B、C为三个实测点，其中A、B为同一条线上相邻测点，A、C为相邻线上同一测点。以A、B、C构成最佳三角形，其对应的三条边分别为a、b、c，由于三个点均为实测点，其对代插点的控制能力相同。在c，a上分别取点D、E，令BD=BE=r，D点的插值结果受A、B点的数据的控制，E点的插值结果受B、C控制。现不断变化r值观察D、E的受控情况：当r趋于0时，D、E均只受B控制，受控制程度相同；随着r不断变大，D、E受B的控制不断减小并分别渐渐开始受A、C的控制，总的受控程度均渐渐降低。由于AD