试件断裂对万吨级多功能结构试验系统隔振层影响的数值分析
2016-04-21李国强孙建运同济大学土木工程防灾国家重点实验室上海0009中国建筑股份有限公司技术中心北京0300
李国强, 王 鹏, 孙建运(.同济大学 土木工程防灾国家重点实验室,上海 0009; .中国建筑股份有限公司技术中心,北京 0300)
试件断裂对万吨级多功能结构试验系统隔振层影响的数值分析
李国强1, 王鹏2, 孙建运2(1.同济大学 土木工程防灾国家重点实验室,上海200092; 2.中国建筑股份有限公司技术中心,北京101300)
摘要:万吨级多功能结构试验系统是中国建筑股份有限公司研制的重型结构试验设备,试验系统的综合功能和加载能力为世界同类设备之最。为减少试验系统对周边办公区域的影响,在设备的基座下面设置了隔振层。采用ANSYS瞬态动力学分析方法,针对试件断裂对万吨级多功能结构试验系统隔振层的冲击影响进行了分析,提取了试验系统基座底部边界角点的X、Y、Z方向位移和单个隔振器的Z方向受力时程曲线,对比分析了不同卸载时间对隔振响应的影响,并校核了隔振器的安全性,对模拟试件断裂的卸载时间提出了建议。针对不同隔振器数量布置的隔振层,计算了试件突然断裂时隔振效果的区别,提出了隔振器数量的建议。
关键词:断裂;冲击;隔振器;试验系统
万吨级多功能结构试验系统,是中国建筑股份有限公司技术中心大型结构工程实验室研制的试验设备。该试验系统垂向加载能力最大值为10 800 t,具备水平双向加载能力,试验空间可调,主要用来进行结构构件和大型隔震支座在静力、动力荷载作用下的响应和破坏模式研究,能够实现巨柱单向压缩、巨柱压剪、巨柱压剪扭、大型剪力墙压剪、梁柱节点试验、复杂空间节点试验、隔震支座压剪等试验,建成后将成为世界上加载吨位最大的多功能试验系统。万吨级多功能结构试验系统的基座下部设置了隔振层,以减少试验过程中对周围办公区域的影响。目前,对仪器设备采取隔振措施时,应根据隔振要求,隔振材料和隔振器的性能、适用条件等作全面考虑,选用适当的隔振器才能达到预期的隔振效果[1-3]。万吨级多功能结构试验系统的隔振设计目标,主要考虑以下几个方面:试验系统对地基基础的传力不能超过地基承载力;基座位移不能超过一定限值,保证试验系统基座底部液压管路安全;避免试验系统的振动过大影响周边环境。
对于试验系统来说,试验过程中可能发生试件突然断裂的情况,这会对隔振层造成冲击作用,因此需要对隔振层的安全性能进行评估。国内的研究学者关于冲击作用对隔振层影响的研究,主要有两种思路。一些研究学者通过将设备的不同部分,合理简化成多刚体与弹簧的模型,利用振型叠加法、时间积分法进行冲击响应的研究,这种方法的优点是计算效率高,但因为没有考虑设备的变形,存在一定的局限性。比如,刘永明[4]进行了多层隔振系统冲击响应研究,庞剑[5]进行了具有刚度非线性双层隔振系统的冲击响应研究。另一种思路,是建立有限元模型,输入已知的冲击荷载,分析隔振层的响应。比如,陶懿[6]进行了双层隔振系统冲击响应的数值模拟。但是,对于隔振层在试件突然发生断裂造成冲击作用下的响应模拟,还较少见诸文献,而这样的数值模拟对保证试验系统隔振设计的安全具有重要意义。
本文旨在针对试件受到垂向压缩时突然发生断裂或压溃,对试验系统隔振层造成的冲击作用进行数值模拟,并分析基座底部边界角点的位移时程曲线和单个隔振器的受力。该数值模拟方法具有一般性,适用于试验系统隔振层在试件发生断裂时安全性能的预测和评估。研究结果可为万吨级多功能结构试验系统隔振层的安全性能提供评估,也对今后校核其他试验系统隔振层的设计安全提供了方法和思路。
1试验系统及隔振层介绍
万吨级多功能结构试验系统主要包括加载框架系统和液压控制系统。加载框架系统主要包括:顶梁、移动横梁、框架立柱、基座、作动器安装支架等。加载框架系统三维示意图如图1所示。
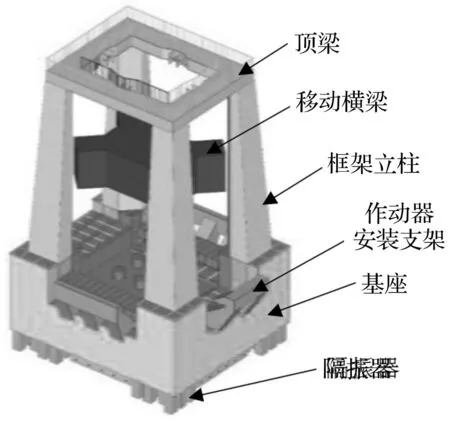
图1 加载框架系统示意图Fig.1 The frame of FAST
加载空间最大高度为10 m(Z向),垂向最大加载能力为10 800 t,水平X方向最大加载能力为600 t,X方向最大位移为1.5 m,水平Y方向最大加载能力为900 t,Y方向最大位移为0.5 m。
试验系统的基座下部设置隔振层,隔振层采用弹簧隔振器,单个隔振器竖向刚度为74.34 kN/mm,水平刚度为57.7 kN/mm,竖向阻尼为300 kNs/m,水平阻尼为600 kNs/m。隔振层共使用52个隔振器,每个角部布置13个,布置方案如图2所示。根据弹簧隔振器的技术要求,单个隔振器最佳竖向承载力为120 t,极限竖向承载力为150 t,最大竖向位移为20 mm。因为油源管路从试验系统的基座内部穿过,为了防止油源管路发生破坏,要求试验系统基座在发生振动时的各方向绝对位移幅值不超过8 mm。

图2 隔振器示意图及布置方案Fig.2 Vibration isolator and its arrangement
2有限元模型
万吨级多功能结构试验系统的有限元模型采用ANSYS软件建立。该模型采用shell181单元模拟钢结构板件,Solid185单元模拟基座中的混凝土。钢结构采用Q460钢材,混凝土采用C60标号。考虑到试验系统的加载框架在试验中均处于线弹性阶段,模型中各材料均采用弹性本构关系。隔振层的模拟采用Combine14弹簧单元,设置在隔振器安装区域的所有节点上,并将隔振层的总刚度和总阻尼平均分配到弹簧单元上。
首先计算了有限元模型的自振特性,表1给出了有限元模型的前三阶自振频率,图3~图5表明了试验系统的前三阶模态。

表1 有限元模型前三阶自振频率

图3 试验系统第一阶模态(水平x方向)Fig.3 The first mode of FAST(horizontal X)

图4 试验系统第二阶模态(水平Y方向)Fig.4 The second mode of FAST(horizontal Y)
图5 试验系统第三阶模态(竖直Z方向)Fig.5 The third mode of FAST(vertical Z)
3试件断裂冲击响应的模拟
试验系统在进行逐步加载并保持荷载稳定的过程中,系统的各个组成部分会发生变形,并储存了大量应变能。当试件突然断裂时,荷载会突然卸除,试验系统储存的应变能会迅速释放,造成冲击作用。
采用荷载步的方法模拟荷载的突然卸除,荷载步如图6所示。0-t1:荷载施加阶段,线性施加垂向荷载,达到试验系统的最大垂向加载能力10 800 t;t1-t2:荷载持续阶段,垂向荷载保持10 800 t;t2-t3:卸载阶段,垂向荷载快速减小到0,模拟试件突然发生断裂;t3-t4:卸载后持续阶段,试验系统因为受到突然卸载造成的冲击作用而发生振动。整个荷载步阶段均考虑重力荷载的作用。
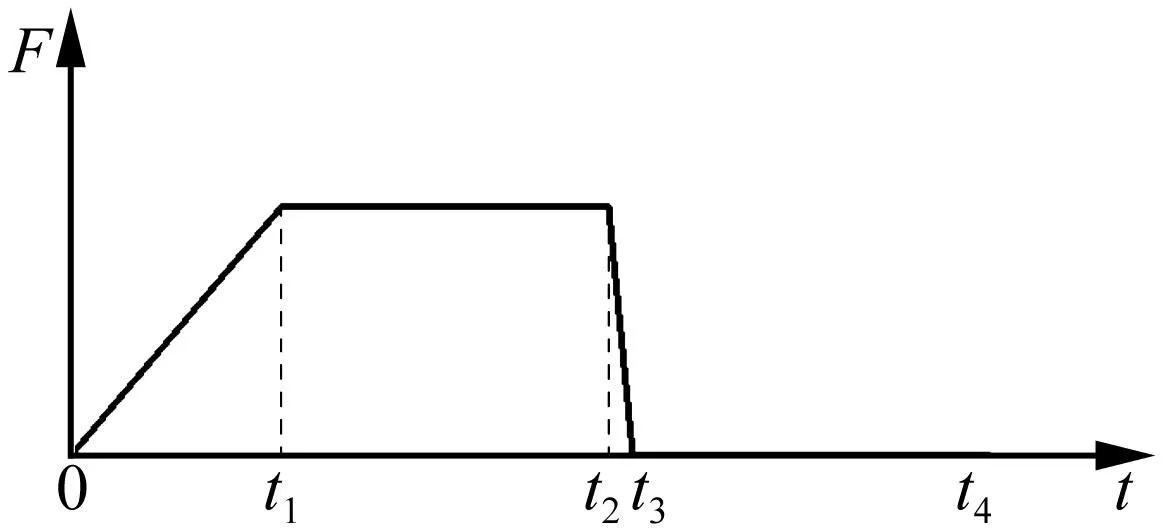
图6 荷载步示意图Fig.6 The load step
王新敏[7]进行了与图6类似荷载步的计算。赵应龙[8]在进行船舶隔振系统的冲击响应计算时,首先采用模态分析,对比有限元计算结果和试验结果的频率,然后利用有限元瞬态动力学分析方法,计算冲击作用。因此本文采用ANSYS瞬态动力学分析方法进行求解。瞬态动力学分析方法,是用于确定结构在承受任意的随时间变化载荷作用下的位移、应变、应力的计算方法[9]。ANSYS在求解时使用Newmark时间积分方法,在离散的时间点上求解基本的运动方程。两个连续时间点之间的时间增量为积分时间步长,积分时间步长的选择对于计算结果的精度有较大影响,而固有频率对积分步长的选择十分有用。因为本文关注隔振层X、Y、Z三个方向的响应,在积分步长的选择上,仅考虑三阶以内的频率影响。
由于结构的动力学响应可以看作是各阶模态响应的组合,积分时间步长应小到能够解出对整体响应有贡献的最高阶模态。并且,对于Newmark时间积分方案,已经发现当时间步长取值20倍最高频率时会产生比较合理精度级的解,合理的时间积分步长可以用下式计算[7]。
(1)
式中:f为模型最高阶的自振频率
依据表1的前三阶频率计算结果,利用式(1),时间积分步长要取小于0.012 s。因此分析中对于加载阶段、荷载维持阶段、卸载后振动阶段的时间积分步长取0.01 s,是满足要求的。对于t2-t3的卸载阶段,考虑到卸载时间非常短,积分步长取为卸载时间的1/10。
4隔振层响应分析
根据图6所示的荷载步曲线,将垂向荷载施加在试验系统的移动横梁和基座上,荷载方向及位置如图7所示。为了模拟试件断裂时荷载的突然卸除,关键是卸载时间的合理选取,不同类型的试件发生断裂时,可能会出现不同的卸载时间,对试验系统造成不同的冲击作用。下面分别假设卸载时间为0.1 s、0.01 s、0.001 s,研究不同的卸载时间对试件断裂造成冲击响应的影响,荷载步的其他相关时间设置如表2所示。
选取试验系统基座底部边界角点,如图7所示红色标记点A,分析在不同的卸载时间下,点A的X、Y、Z方向位移时程曲线,以及A点位置单个隔振器的Z向力,分析结果见图8~图11。张志[10]对隔振系统的冲击响应进行了研究,通过对比图8~图10的位移冲击响应趋势,可以定性判断结果的正确性。

表2 荷载步时间设置(单位:s)

图7 荷载施加示意图Fig.7 The position of load in FEA model

图8 不同卸载时间下点A的X方向位移时程Fig.8The displacement time history of point A in X direction

图9 不同卸载时间下点A的Y方向位移时程Fig.9 The displacement time history of point A in Y direction

图10 不同卸载时间下点A的Z方向位移时程Fig.10 The displacement time history of point A in Z direction
图8为点A的X方向位移时程曲线,在0~1 s加载阶段,X方向位移逐渐增大;在1~2 s荷载稳定阶段,X方向位移基本保持在-0.2 mm左右,并保持稳定;突然卸载后,X方向位移会发生振荡,不同的卸载时间会造成振动幅值的不同。当卸载时间为0.1 s时,最大振幅为0.2 mm。当卸载时间为0.01 s时,最大振幅为0.3 mm。当卸载时间为0.001 s时,最大振幅为0.4 mm。卸载时间越短,X向位移的振动幅值越大。
图9为点A的Y方向位移时程曲线,在0~1 s加载阶段,Y方向位移逐渐增大;在1~2 s荷载稳定阶段,Y方向位移基本保持在0.14 mm左右,并保持稳定;突然卸载后,Y方向位移会发生振动,不同的卸载时间会造成振动幅值的不同。当卸载时间为0.1 s时,最大振幅为0.13 mm。当卸载时间为0.01 s时,最大振幅为0.15 mm。当卸载时间为0.001 s时,最大振幅为0.2 mm。卸载时间越短,Y向位移的振动幅值越大。
图10为点A的Z方向位移时程曲线,在0~1 s加载阶段,Z方向位移逐渐增大;在1~2 s荷载稳定阶段,Z方向位移基本保持在14 mm左右,并保持稳定;突然卸载后,Z方向位移会发生振动,不同的卸载时间下Z方向位移的振动幅值基本一致,最大振幅在3 mm以内,满足试验系统油源管路对基础位移8 mm的要求。
图11为点A位置处单个隔振器的Z方向受力时程曲线,在0~1 s加载阶段,单个隔振器的Z方向力逐渐增大;在1~2 s荷载稳定阶段,Z方向力达到100 t左右,并保持稳定;突然卸载后,Z方向力会发生振动,不同的卸载时间下Z方向力的振动曲线基本一致,Z方向力最大达到120 t,满足弹簧隔振器的技术要求。
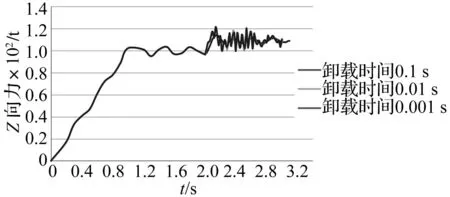
图11 不同卸载时间下点A的单个隔振器Z方向力时程Fig.11 The force time history of point A in Z direction
5不同隔振器数量的影响
考虑到弹簧隔振器的技术参数已经确定,隔振器的数量和布置成为了隔振层设计的关键。根据图2隔振器的布置示意图,由于基座底部有十字形加劲区域的存在,隔振器需要对称布置在基座底部的四个角部。由于空间限制,隔振器最多布置数量为60个,考虑到隔振器布置的对称性,调整隔振器的数量分别为48、52、56、60,研究不同隔振器数量对于隔振效果的影响。
对于不同隔振器数量的模型,隔振效果的评价指标是:当试件发生断裂,垂向荷载突然卸除时,有限元模型的基座底部角点A的X、Y、Z方向位移时程曲线和单个隔振器的Z向受力时程曲线。分析方法统一ANSYS瞬态动力学分析方法,卸载时间取为0.1s,分析结果见图12~图15。
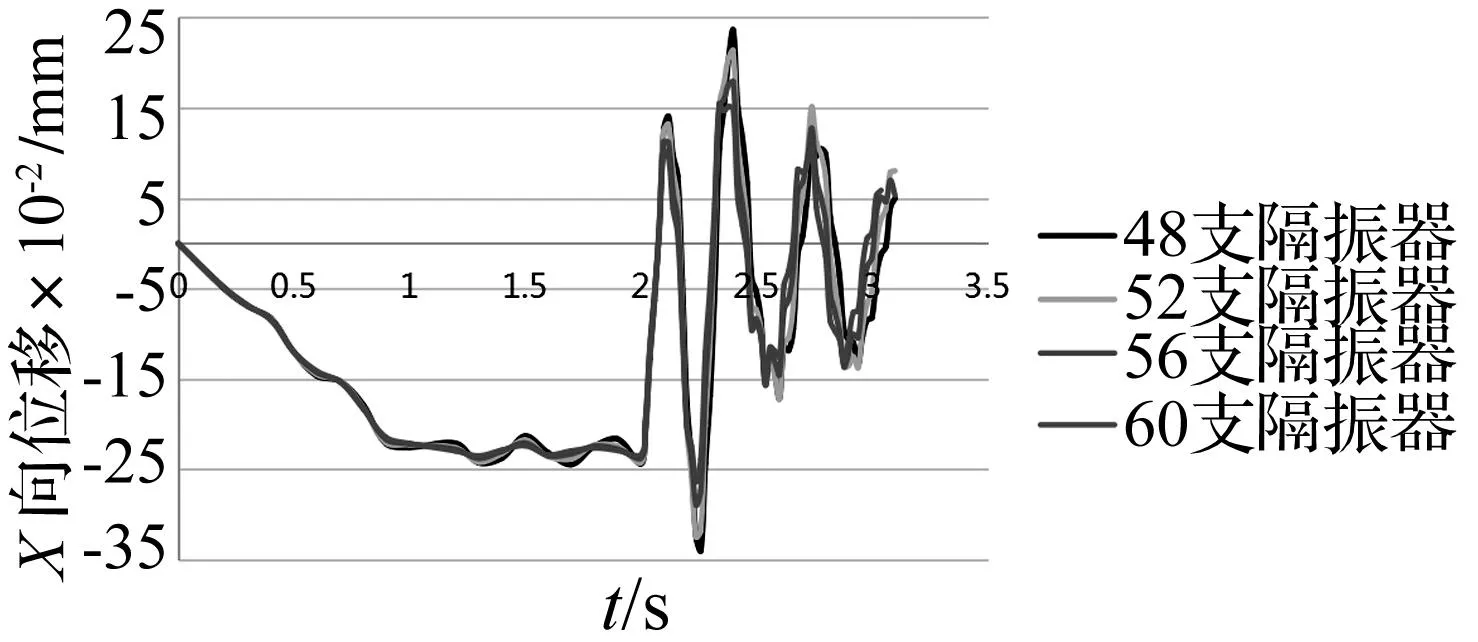
图12 不同隔振器数量布置下点A的X方向位移时程Fig.12 The displacement time history of point A in X direction on different number of vibration isolator

图13 不同隔振器数量布置下点A的Y方向位移时程Fig.13 The displacement time history of point A in Y direction on different number of vibration isolator

图14 不同隔振器数量布置下点A的Z方向位移时程Fig.14 The displacement time history of point A in Z direction on different number of vibration isolator

图15 不同隔振器数量布置下点A的单个隔振器Z方向受力时程Fig.15 The forcet time history of point A in Z direction on different number of vibration isolator
通过对比不同隔振器数量布置下点A的隔振效果,可以得出以下结论。① 对于X方向和Y方向水平位移时程曲线,在0~2 s阶段,不同隔振器数量布置方案之间的时程曲线基本重合。在2 s末发生垂向荷载的突然卸除后,不同隔振层之间的水平位移时程曲线差别也很小,隔振器数量的改变对于水平方向的振动影响不大。② 对于Z方向位移时程曲线,在0~2 s阶段,隔振器数量越少,Z方向位移越大。在2 s末发生垂向荷载突然卸除后,隔振器数量越少,Z方向位移的振动越大。当隔振器数量为48时,最大振动幅值为3 mm,仍然符合基座振动的位移要求。③ 对于单个隔振器的Z方向受力时程曲线,在0~2 s阶段,隔振器数量越少,Z方向受力增长越快,稳定后的Z方向力也越大。在2 s末发生垂向荷载突然卸除后,隔振器数量越少,单个隔振器的Z方向受力振动越大。
考虑到弹簧隔振器的技术要求,最佳竖向承载力要求120 t,最大竖向位移为20 mm。对比不同隔振器数量的四种隔振层的计算结果,不同隔振层的位移时程均能满足技术要求,不同隔振层的单个隔振器Z方向受力计算结果如表3所示。
根据表3,当隔振器数量为48时,垂向荷载消失后的振动过程中,单个隔振器的Z向力大于120 t,不满足技术要求。当隔振器数量为60时,单个隔振器的Z方向受力始终小于100 t,没有充分发挥隔振器的性能。综合以上考虑,建议隔振器数量为52个或者56个。目前的设计方案为52个隔振器,如果考虑增大万吨级多功能结构试验系统隔振层的安全储备能力,防止出现个别隔振器失效的情形,建议考虑安装56个隔振器。
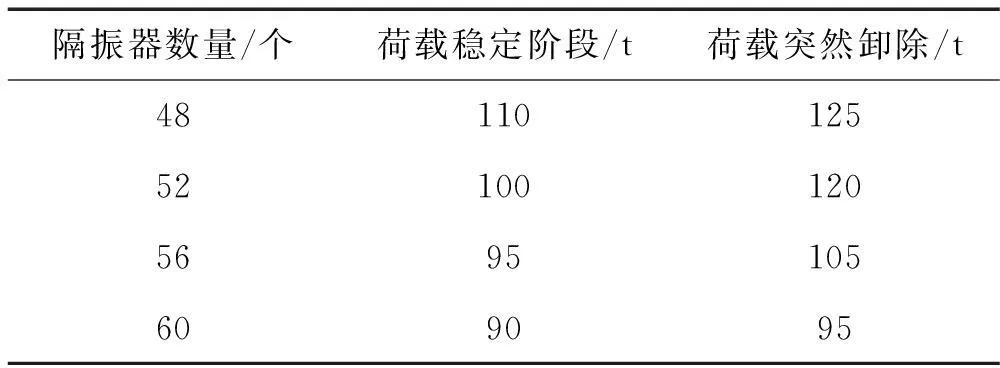
表3 不同隔振器数量下单支隔振器的受力值
6结论
(1) 利用荷载步模拟试件突然断裂造成的冲击作用时,卸载时间越小,X和Y方向的水平位移时程曲线在卸载后的振动幅值越大;Z方向位移时程曲线和单个隔振器的Z方向受力在卸载后的振动幅值,受到卸载时间的影响较小。综合来看,对试验系统的隔振层进行冲击作用的数值模拟时,建议取卸载时间为0.1 s进行分析。
(2) 基座底部角点的位移和单个隔振器Z方向受力均满足技术要求,验证了万吨级多功能结构试验系统隔振层设计的安全性。该数值模拟方法,可以为将来其他试验设备的隔振层冲击响应分析提供参考。
(3) 隔振器的数量对隔振效果有显著影响,数量过多,无法充分发挥每支隔振器的功能,造成浪费;数量过少,试件断裂时隔振器的受力过大,超过隔振器的技术要求,容易造成损坏。根据分析,本文建议隔振器的数量为52个或56个。
参 考 文 献
[ 1 ] 王平安,王杰贤.精密仪器工作台的隔振设计[J].西安建筑科技大学学报,1999,31(3):263-267.
WANG Ping-an, WANG Jie-xian. The design of isolation vibration for precision instrument table[J]. J.Xi’an Univ. of Arch. &Tech, 1999,31(3):263-267.
[ 2 ] 翁俊.隔振系统振动的传递特性分析及振动评价研究[D].哈尔滨:哈尔滨工业大学,2012:2-5.
[ 3 ] 李银川,方开翔.隔振器参数对船舶动力机械系统隔振性能的影响分析[J].江苏科技大学学报:自然科学版,2006,20(5):10-14.
LI Yin-chuan, FANG Kai-xiang. Effects of isolation parameters on performance of vibration isolation system for power machinery in ship[J]. Journal of Jiangsu University of Science and Technology:Natural Science Edition,2006,20(5):10-14.
[ 4 ] 刘永明,沈荣瀛, 严济宽. 多层隔振系统冲击响应研究[J].噪声与振动控制, 1996,20(3): 2-8.
LIU Yong-ming, SHEN Rong-ying, YAN Ji-kuan.Research on response caused by the impact of multilayer vibration isolation[J]. Noise and Vibration Control,1996,20(3): 2-8.
[ 5 ] 庞剑,严济宽.具有刚度非线性双层隔振系统的冲击响应[J].武汉造船,1993,25(5):1-5.
PANG Jian, YAN Ji-kuan. Response caused by the impact of double-layer vibration isolation system[J].Wuhan Ship building, 1993,25(5):1-5.
[ 6 ] 陶懿,周海亭.双层隔振系统冲击响应数值模拟方法的研究[J].噪声与振动控制,2005,25(3):3-7.
TAO Yi, ZHOU Hai-ting. Research on numerical simulation calculation of shock response in double-layer vibration isolation system[J]. Noise and Vibration Control,2005,25(3):3-7.
[ 7 ] 王新敏,工程结构数值分析[M].北京:人民交通出版社,2007:519-530.
[ 8 ] 赵应龙,何琳,黄映云,等.船舶浮筏隔振系统冲击响应的时域计算[J].噪声与振动控制,2005,25(2):15-19.
ZHAO Ying-long, HE Lin, HUANG Ying-yun, et al.The computation of shock response of marine floating raft shock-resistant system in the time domain[J].Noise and Vibration Control,2005,25(2):15-19.
[ 9 ] 张秀辉,ANSYS有限元分析从入门到精通[M].北京:机械工业出版社,2012:340-343.
[10] 张志,张兆会,董森,等.橡胶双层减振与隔振系统冲击响应研究[J].振动与冲击,2013,32(23):126-130.
ZHANG Zhi, ZHANG Zhao-hui,DONG Sen,et al. Schock Response of a rubber double-deck vibration isolation system[J]. Journal of Vibration and Shock,2013,32(23):126-130.
Numerical analysis for effects of specimen fracture on facility of advanced structural testing (FAST)
LIGuo-qiang1,WANGPeng2,SUNJian-yun2(1. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China;2. China State Construction Technical Center, Beijing 101300, China)
Abstract:The facility of advanced structural testing (FAST) is planned to be manufactured by China State Construction Engineering Corporation Ltd (CSCEC). The maximum allowable value of vertical force is 10800t. It is necessary to consider the impact caused by the sudden fracture of specimen on the surrounding area. Here, the design of FAST and its isolation system were introduced briefly. The finite element simulation for the impact cause by the sudden fracture of specimen on FAST was conducted. Using the transient dynamic analysis method of Ansys, the loading steps were used to simulate sudden fracture of a specimen. Time-history curves of displace ments in X, Y and Z directions of the isolator and the isolator’s force in Z direction were used as the evaluation indexes for the impact effects. Through changing the unloading time, the effects of unloading time on the vibration responses were analyzed and compared. The requirements for displacement and force of the isolator were checked. Finally, some suggestions about unloading time to simulate fracture of specimen and the number of isolators were proposed.
Key words:fracture; impact; vibration isolator; testing system
中图分类号:TU375
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.05.035
通信作者王鹏 男,硕士,1989年12月生
收稿日期:2015-01-23修改稿收到日期:2015-03-20
第一作者 李国强 男,博士,教授,1963年2月生
