多跨转子系统流体引发自激振动稳定性分析

赵　倩， 许　琦， 姚红良， 闻邦椿(东北大学 机械工程与自动化学院，沈阳　110819)



多跨转子系统流体引发自激振动稳定性分析

赵倩， 许琦， 姚红良， 闻邦椿(东北大学 机械工程与自动化学院，沈阳110819)

摘要：以实际压缩机组多跨转子系统为研究对象，针对由间隙气流激振力引起的失稳问题，进行Alford力作用下多跨转子系统的动力学及稳定性分析。针对该类模型自由度多的特点，采用固定界面模态综合法降维措施与New-mark-β法相结合，提高了求解效率。研究交叉刚度、工作转速等对转子涡动的影响，以及多跨转子系统中Alford力的传递作用；通过以时间历程曲线为稳定性判据，进行不同交叉刚度、阻尼、刚度系数下的稳定性分析。结果表明，交叉刚度的增大会加重转子涡动，降低系统的稳定性；系统阻尼和刚度的增大可提高稳定性；失稳交叉刚度与支承的交叉刚度存在一定关系，当其大于支承最小交叉刚度且接近支承最大交叉刚度时，系统容易失稳。

关键词：多跨转子；Alford力；交叉刚度；自激振动；稳定性分析

近年来，随着透平旋转机械向着超大型化、低能耗化与高可靠性方向发展，叶轮转速和性能逐步提高，叶轮轴大多采用柔性轴设计，工作转速在一阶甚至二阶临界转速以上；高效率则要求必须缩小转静子间隙，叶片的气动负荷也日益增大。这些都可能影响转子系统的稳定性，尤其是产生自激振动，且不能采用动平衡的方法来消除。

由于小间隙、高转速、大压比、以空气或蒸汽作为介质等复杂的工作条件决定了机组中存在复杂的激励源。此类转子系统有两类主要的失稳激励源：油膜力和间隙气流激振力。目前关于非线性油膜力模型及其对转子运动稳定性的影响方面已有较多研究，能够较好地分析油膜失稳规律，而对间隙气流激振力的失稳规律研究较少。间隙气流激振引起的自激振动严重影响机组的安全稳定运行，由于自激振动，叶轮等关键部件受力增大，经常会造成疲劳破坏，在一定条件下会引起转子的失稳。因此，研究间隙气流激振力作用下多跨转子系统的动力学行为及失稳规律具有重要的理论和现实意义。

以往研究多集中于间隙气流激振力模型的研究。Thomas[1]研究了燃气轮机的不稳定性，并提出由偏心转子引起的非对称半径间隙可能导致失稳力，称之为间隙激振力。随后，Alford[2]在研究航空发动机稳定性时发现了类似的现象，间隙激振这一问题才引起人们的足够重视，并在习惯上称为Alford力。然而两人的研究结果都是根据叶轮的局部效率损失得到的，在实际应用中存在许多缺陷。之后很多学者做了修正工作，如Hubert根据无冠叶栅试验，提出了叶尖间隙损失的一种指数关系来代替Alfold公式采用的线性关系；为了进行验证，Urlichs[3]对涡轮发动机进行了实验研究；Vance[4]用鼓风机进行静止偏心时作用于叶轮上横向力的测试，证实了Alford力的存在。国内也有不少学者对其进行了改进，如杨建刚等[5]将其分为静态力和动态力两部分考虑，改进了传统的Alford力模型；柴山[6]从流体力学出发，应用动量定理对气流间隙激振力进行了多方面的研究；丁学俊[7]提出了Alford力中效率系数的一种计算方法；骆名文等[8]对大型汽轮机气流激振的研究现状做了系统总结与展望。

然而关于Alford力作用下转子系统稳定性方面的研究并不多，且大都针对简单转子。如Kim等[9-10]采用Jeffcott转子，杨建刚[5]针对某一单跨高压转子进行稳定性分析，而工程实际中存在的机组往往为多跨复杂转子系统。因此，本文以多跨转子系统为研究对象，针对该类模型自由度多的特点，采用固定界面模态综合法降维；研究交叉刚度和转速对转子涡动的影响以及多跨转子系统中Alford力的传递作用；提出以时间历程曲线为稳定性判据，进行了不同交叉刚度、阻尼、刚度系数下转子系统的失稳规律研究。

1模型建立方法

1.1Alford力及交叉刚度计算

由于制造安装问题或不平衡力的作用，叶轮与气缸会产生相对偏心，使得叶尖间隙沿圆周分布不均匀。因此，叶片上的周向气动力除合成一个转矩外，还合成一个作用于转子轴心的横向力，称为间隙气流激振力或Alford力。该激振力[2]可表示为

FA=[τβ/(DH)]e

(1)

式中，τ为作用在叶片上的扭矩；D为叶片中径；H为叶片高度；e为偏心距；β为激振力的效率系数。

由其引起的交叉刚度项为

Kyx=τβ/(DH)

(2)

由于β是一个与叶轮结构、扭矩大小等有关的量，而不是一个常数，很难选取合适的值。近年来，关于β值的符号和大小，国内外学者已做了较多的研究，但结论不一，且相互之间的偏差较大。大部分还是以Alford给出的数值作为参考。

关于Alford力引起的交叉刚度，一直以来仍没有一个普遍适用的定量计算方法。由于本文旨在分析Alford力及其引起的交叉刚度对多跨转子系统稳定性的影响，因此关于Alford力及交叉刚度的计算在此未做深入讨论，以前人的研究结果作为参考。

1.2转子系统建模

设转子系统由弹性轴段单元组成，如图1所示。忽略轴向变形，每节点包括两个移动方向的自由度和两个旋转方向的自由度。每个单元上的广义坐标如式

[xAyAθxAθyAxByBθxBθyB]T

(3)

图1　欧拉梁单元模型Fig.1 The model of Euler beam element

采用有限元建模方法，间隙气流激振转子系统的运动微分方程为

(4)

式中，M、C、K分别为质量、阻尼、刚度矩阵；x为位移向量；F为外激励向量；FA为Alford力向量。

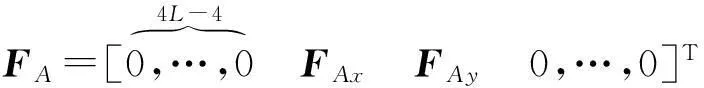
本文采用文献[5]中的Alford力模型，将其分解为静态力和动态力两部分，具体表达式为

(5)

式中，δx，δy分别为x和y方向的静偏心；kA为Alford力引起的交叉刚度项。

2固定界面模态综合法降维

对多跨转子系统进行振动分析，其动力学模型往往能达到成千上百个自由度。为了提高计算效率，可以采用固定界面模态综合法(Component Mode Synthesis, CMS)进行自由度的降维[11]。将式(4)划分为线性和非线性(即间隙气流激振位置)两部分，其中上部分为线性部分，下部分为非线性部分

(6)

假设非线性位置处的自由度固定，计算剩余自由度组成系统的模态，并取其中可能参与响应贡献大的模态组成固定界面主模态集

(7)

假设给某个界面自由度单位位移，保持其他界面自由度为0，形成该自由度下的约束模态

(8)

对每个界面自由度按上式操作，形成约束模态集

(9)

由固定主模态集和约束模态集组合可得系统的模态矩阵

(10)

因此，将式(8)变换为模态坐标下的振动方程

(13)

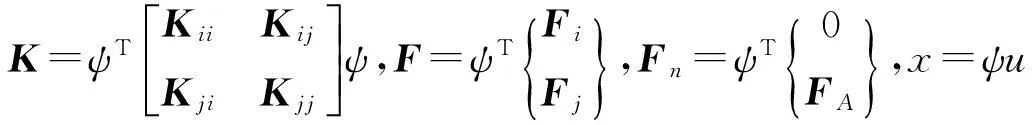
采用数值法求得方程(11)在模态坐标下的解u，利用x=ψu返回到原物理坐标，可得原系统的动态响应。

可见系统的降维主要是依靠主模态集的缩减实现，主模态集中模态取得越少，所得模型的自由度越少，但是可能会影响所求得响应的精度。

3数值仿真与分析

图2为简化后的双跨转子系统有限元模型，叶片部位采用集中质量单元，详见表1。共划分137个节点，136个单元，Alford力作用于压缩机某级叶片上。转子密度ρ= 7 850 kg/m3，弹性模量E= 2.1×1011N/m，泊松比ν= 0.3。压缩机支承位于节点4和65处，汽轮机支承位于节点72和120处，支承刚度及阻尼根据轴颈尺寸和润滑油型号由软件XlRotor计算确定，详见表2。

表1　集中质量节点

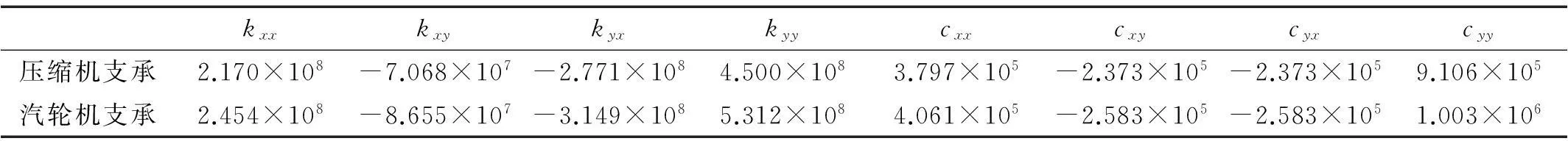
表2　轴承的支承刚度(N/m)和阻尼(N·s/m)

转子系统的前三阶固有频率和临界转速分别为19.87 Hz、31.75 Hz、76.22 Hz和1 215.8 r/min、1 998.3 r/min、4 969.3 r/min；额定转速3 400 r/min，高于二阶临界转速。

图2　双跨转子动力学模型Fig.2 Dynamic model of a dual-span rotor system

3.1交叉刚度和转速的影响

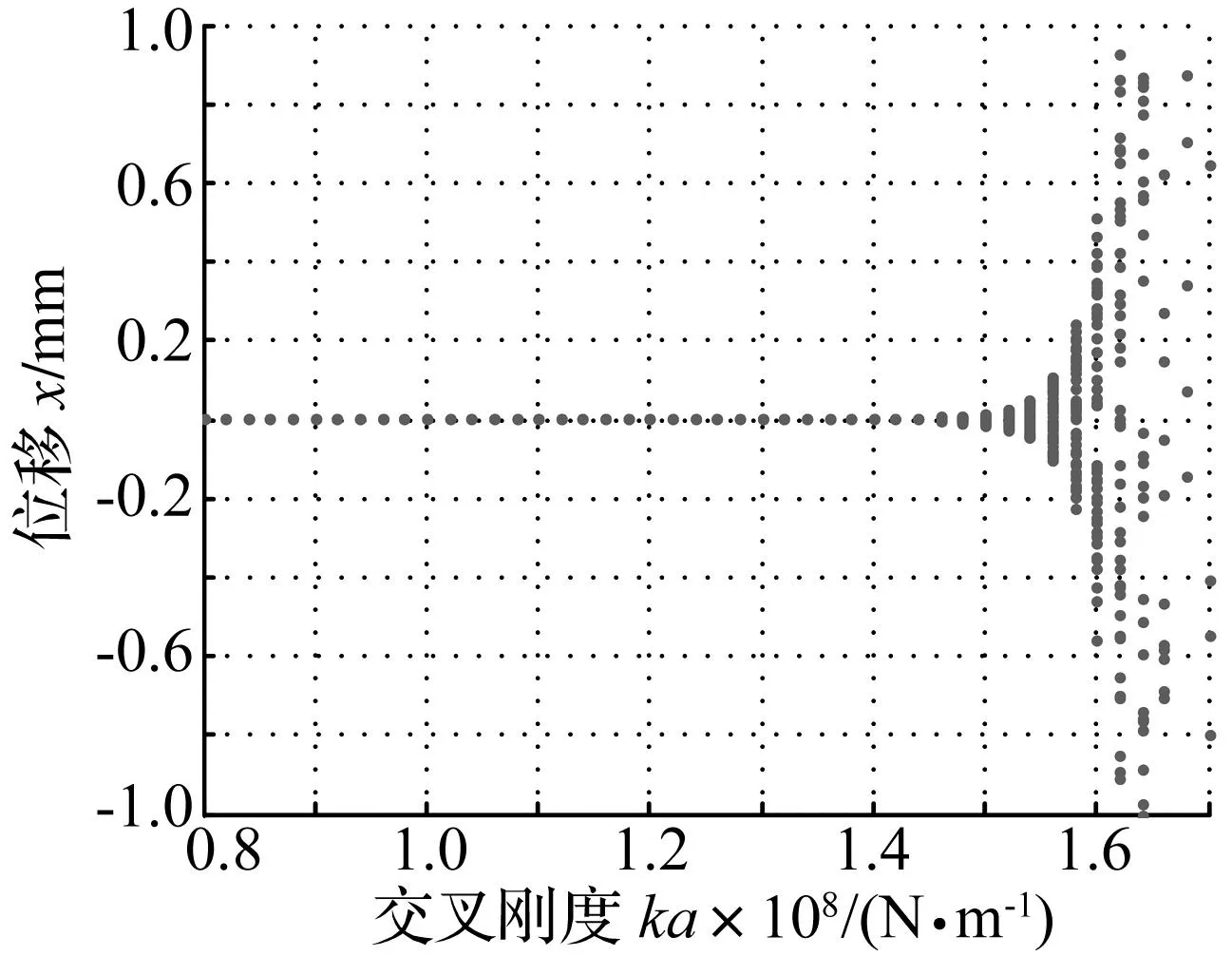
采用Newmark-β法结合CMS降维(取30阶主模态)进行分析。设角速度为300 rad/s，图3比较了交叉刚度变化时的频谱：当ka= 1.4×108N/m时，转子出现涡动，随着ka的进一步增大，频谱中的低频成分增大，转子涡动加重。取ka= 1.4×108N/m，图4为转速变化时的频谱：随转速提高，低频成分幅值增大，且低频均锁定于127 rad/s，接近转子系统第一阶临界转速。

3.2Alford力在多跨转子系统中的传递作用

表3列出了转子系统中不同位置处的频率成分幅值。可以看出，叶轮上任一位置存在Alford力，整机转子各个位置均产生涡动；相比于压缩机转子上Alford力振源位置处的振动，联轴器上的振幅减小了约0.5倍，汽轮机转子上的振幅减小了两个数量级；转子各个位置呈现相似的振动特性，各跨转子之间会产生相互影响及Alford力的传递，因此，在研究间隙气流激振稳定性时，应考虑多跨转子系统。

图3　不同交叉刚度的频谱图Fig.3 Spectrograms in different cross stiffness

图4　不同转速下的频谱图Fig.4 Spectrograms in different rotating speed

位置工作频率幅值/mm涡动频率幅值/mm压缩机叶片(Alford力处)2.3×10-21.0×10-3压缩机转子1.7×10-28.3×10-4汽轮机叶片7.0×10-43.3×10-5汽轮机转子2.4×10-41.9×10-5联轴器6.5×10-33.5×10-4

3.3Alford力作用下多跨转子系统的稳定性分析

本研究根据时间历程曲线判断系统的运行状态及稳定性。如图5所示，转子系统的动力学响应有以下几种振动情况。图5(a)中，系统趋于稳定运行，Alford力不足以引起转子系统的涡动；图5b中，系统由于Alford力作用产生转子涡动；图5c中，由于Alford力引起的负阻尼作用超过系统的阻尼，振动幅值迅速增大，系统发散，为不稳定运行。

图5　三种不同的运行状态Fig.5 Three different operation states

根据该稳定性判断依据，分析不同参数(交叉刚度、阻尼系数、刚度系数)变化时的稳定性区域，如图6所示。

图6(a)中，随着交叉刚度的增大和转速的提高，稳定区域逐渐减小，当交叉刚度增至1.55×108N/m时，系统在任一转速下均失稳；图6(b)中，随着阻尼系数的增大，稳定区域越来越大，涡动区域减小，当阻尼系数降至0.85时，系统完全失稳；图6(c)中，稳定区域随着刚度系数的增大而增大，当刚度系数降至0.8时，系统完全失稳。因此，降低交叉刚度，增大系统阻尼和刚度可有效抑制转子涡动，提高系统的稳定性。

另外，对比Alford力引起的交叉刚度ka(图6(a))与表2中支承(即滑动轴承)交叉刚度kxy、kyx可以发现，对于非对称支承即kxy≠kyx且kxy 0.5kyx时，系统失稳；③ 当kxy

图6　不同参数组合下的稳定性区域图Fig.6 Stability regional graphs with different parameters combination

图7为工作转速下以ka为分岔参数的分岔图，在ka= 1.5×108N/m附近时出现分岔，与图6(a)的结果基本一致。

图7　交叉刚度为分岔参数的分岔图Fig.7 Bifurcation diagram with different cross stiffness

4结论

(1) 传统采用对数衰减率分析稳定性，只能判定稳定区和失稳区；本文方法采用时间历程曲线作为稳定性判据，得到转子由于Alford力作用，会随着运行参数的变化，依次经历稳定区-涡动区-失稳区。而涡动区同样为危险区，此时可通过调整相关参数等措施，进行涡动的抑制，防止系统由于严重涡动迈向失稳区，此方法也可用于前期设计阶段中参数的优化设计。

(2) 对交叉刚度、系统阻尼和刚度变化下的稳定性进行了研究：稳定性区域随着交叉刚度的增大而减小，随着阻尼和刚度的增大而增大。因此，降低交叉刚度，增大系统阻尼和刚度可有效抑制转子涡动，提高系统的稳定性。同时，失稳交叉刚度与支承交叉刚度之间存在一定关系。

(3) Alford力对失稳的影响主要取决于交叉刚度的大小，而交叉刚度本身又与工作负载、流量、转速、偏心等诸多参数有关。本文进行了交叉刚度变化下系统的稳定性预测，而对于交叉刚度与偏心等参数之间的定量计算研究不足。今后有待进一步研究的是，交叉刚度与各参数之间的定量关系，以及抑制涡动、提高运行稳定性的参数优化匹配。

参 考 文 献

[ 1 ] Thomas H J. Unstable oscillations of turbine rotors due to steam leakage in the sealing glands and the buckets[J]. Bulletin Scientifique. A.J.M., 1958, 71：223-236.

[ 2 ] Alford J S. Protecting turbo machinery from self-excited rotor whirl[J]. ASME Journal of Engineering for Gas Turbines and Power, 1965, 87(4)：333-343.

[ 3 ] Urlichs K. Leakage flow in thermal turbomachines as the origin of vibration-exciting lateral forces, TT-17409[R]. Washington: NASA, 1977.

[ 4 ] Vance J, Laudadio F. Experimental measurement of Alford’s force in axial flow turbomachinery[J]. Journal of Engineering for Gas Turbines and Power, 1984, 106(3)：585-590.

[ 5 ] 杨建刚，朱天云，高伟. 气流激振对轴系稳定性的影响分析[J]. 中国电机工程学报，1998, 18(1)：9-11.

YANG Jian-gang, ZHU Tian-yun, GAO Wei.Influence of steam induced vibration on the stability of rotor-bearing system[J]. Proceedings of the CSEE, 1998, 18(1)：9-11.

[ 6 ] 柴山，张耀明，曲庆文，等. 汽轮机间隙气流激力分析[J]. 中国工程科学，2001, 3(4)：68-72.

CHAI Shan, ZHANG Yao-ming, QU Qing-wen, et al. The analysis on the air-exciting-vibration force of steam turbine[J]. Engineering Science, 2001, 3(4)：68-72.

[ 7 ] 丁学俊，王刚，黄树红，等. Alford力中效率系数的一种计算方法[J]. 华中科技大学学报:自然科学版，2003, 31(4)：66-68.

DING Xue-jun, WANG Gang, HUANG Shu-hong, et al.Calculation of efficiency factor in Alford’s force[J]. Journal of Huazhong University of Science and Technology:Nature Science Edition, 2003, 31(4)：66-68.

[ 8 ] 骆名文，丁学俊，杨彦磊. 大型汽轮机气流激振研究现状及展望[J]. 热能动力工程，2006, 21(6)：551-555.

LUO Ming-wen,DING Xue-jun, YANG Yan-lei. The status quo and prospect concerning a study on steam flow excitations in large-sized steam turbines[J]. Journal of Engineering for Thermal Energy & Power, 2006, 21(6)：551-555.

[ 9 ] Kim H S, Cho M, Song S J. Stability analysis of a turbine rotor system with Alford forces[J]. Journal of Sound and Vibration, 2003, 260：167-182.

[10] 唐云冰，高德平，罗贵火，等. 叶轮偏心引起的气流激振力对转子稳定性影响的分析[J]. 航空学报，2006, 27(2)：245-249.

TANG Yun-bing, GAO De-ping, LUO Guii-huo, et al. Stability analysis of rotor systems with gas exciting force caused by blade tip clearance[J]. Journal of Acta Aeronautica et Astronautica Sinica, 2006, 27(2)：245-249.

[11] Kawamura S, Naito T, Zahid H M, et al. Analysis of nonlinear steady state vibration of a multi-degree-of-freedom system using component mode synthesis method[J]. Applied Acoustics, 2008, 69(7)：624-633.

Stability of a multi-span rotor system with fluid-induced self-excited vibration

ZHAOQian,XUQi,YAOHong-liang,WENBang-chun(School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China)

Abstract:Turbine rotor systems may lose stability due to Alford forces. Here, dynamic characteristics and stability of a multi-span rotor system for a practical compressor unit subjected to Alford forces were investigated. Newmark-β method combined with the fixed interface component mode synthesis (CMS) dimension reduction approach due to many degrees of freedom of a large scale rotor system was applied to obtain the system’s dynamic response. The computational efficiency was improved obviously. The effects of cross stiffness and rotating speed on rotor whirling and the transmission action of Alford forces in the multi-span rotor system were studied. Taking the system’s time historv response as a stability criterion, stability analysis with different dynamic parameters was performed. It was shown that the rotor whirling aggravates and its stability decreases with increase in cross stiffness; its stability is improved with increase in the system’s damping and stiffness; when the cross stiffness of the system are larger than the minimum cross stiffness of bearings and close to the maximum cross stiffness of bearings, the system is easy to be unstable.

Key words:multi-span rotor; Alford force; cross stiffness; self-excited vibration; stability analysis

中图分类号:TH113.1, O323

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.05.032

通信作者姚红良 男，博士，副教授，1979年10月生

收稿日期：2014-11-19修改稿收到日期：2015-03-05

基金项目：国家重点基础研究发展计划项目(2011CB706504)；国家自然科学基金资助项目(51475085)；研究生科研创新项目(N140306003)

第一作者 赵倩 女，博士生，1989年1月生

E-mail：hlyao@mail.neu.edu.cn