层间过渡约束阻尼结构动力响应的分布参数传递函数解

燕碧娟, 张文军, 李占龙, 孙大刚(太原科技大学 机械工程学院，太原　030024)



层间过渡约束阻尼结构动力响应的分布参数传递函数解

燕碧娟, 张文军, 李占龙, 孙大刚(太原科技大学 机械工程学院，太原030024)

摘要：针对传统约束阻尼结构振动能耗散有限问题，引入“层间过渡层”设计的概念，提出一种层间过渡约束阻尼结构，采用分布参数传递函数法对该结构进行了动力响应分析。经推导，得到了阻尼结构的各阶损耗因子和频率的解析解，并进行了有限元仿真验证，二者计算结果吻合良好。以悬臂阻尼板为例，探讨了过渡层参数行为对其频响特性的影响，结果表明，在结构振动时，过渡层可将变形传递给阻尼层，起到放大阻尼层的剪切变形作用，从而耗散更多的振动能量；同时还讨论了过渡层的厚度、剪切模量、密度与泊松比对结构固有频率和损耗因子的影响，为进一步优化工作打下了良好基础。

关键词：传递函数法；过渡层；约束阻尼；动力响应

在减振结构表面附加阻尼耗能层和弹性约束层，构成传统约束阻尼结构[1-2]，它可将外界的振动能转化为热能进行耗散。然而，在实际应用中，其能量耗散能力经常会受到一定限制[3]。针对该问题，国内外学者做了大量研究工作。Lepoittevin等[4]对约束阻尼梁的最外约束层进行了间隔处理，并基于应变能分析对间隔位置进行了优化；Gao等[5]用压电材料做约束层，来增大阻尼层的剪切变形；孙大刚等[6]采用了双阻尼层和约束层，构成五层管状约束阻尼结构，并成功将五层结构应用于履带车辆的驱动轮中。本文引入“层间过渡层”设计的概念，提出一种层间过渡约束阻尼结构(见图1)，即：在传统约束阻尼结构的基础层与阻尼耗能层结合面处增加过渡缓冲层(其弹性模量和损耗因子介于金属材料和黏弹性材料之间)，减小弹性约束层与阻尼耗能层的耦合，从而增大阻尼层弯曲振动；另一方面，“层间过渡层”的引入，可增加振动冲击能耗散的通道，改善结构阻尼和刚度。

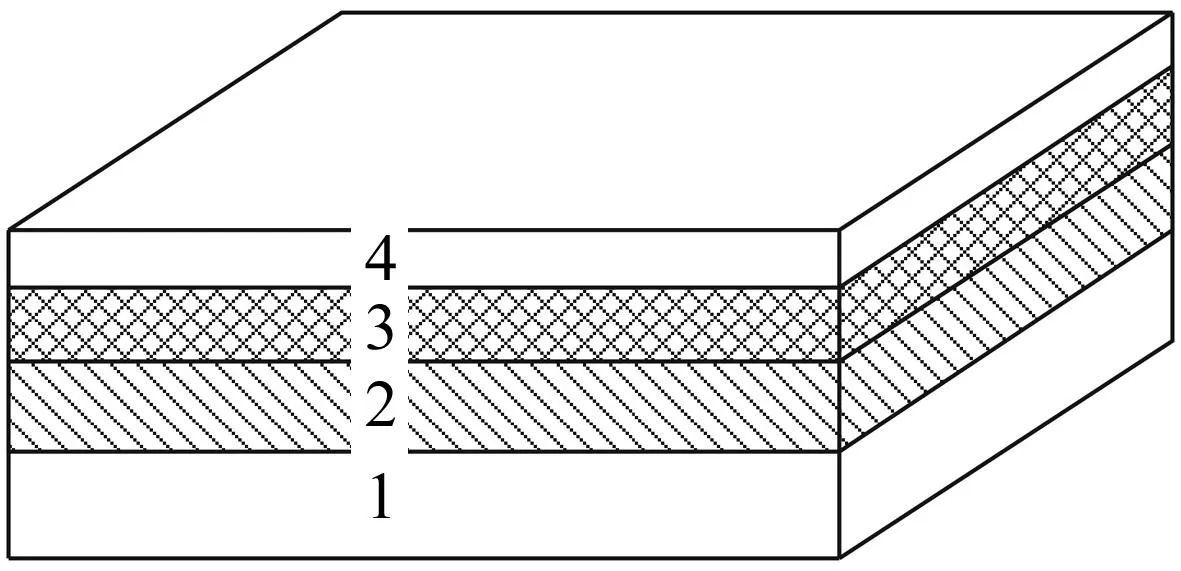
1.基础层　2. 过渡层　3. 阻尼层　4. 约束层图1　 层间过渡约束阻尼板示意图Fig.1 constrained damping plate with transition layer

针对阻尼结构动力响应研究，主要有解析和有限元两种方法[7]。分布参数传递函数法作为一种有效的数值分析方法，得到了许多学者的关注。文献[7]针对四边简支三层约束层阻尼板，采用传递函数方法进行了动力学分析。杨坤等[8]基于哈密顿原理，采用分布参数体系传递函数方法，对复合材料夹层梁进行了动力学响应分析。Yang等[9]形成了一维系统的分布参数传递函数理论，并进行了大量的研究工作，结果表明此解相对于特征函数展开处理法具有明显的优势；Susanto[10]基于分布参数传递函数法对主动压电层合结构梁进行了建模及动力学分析。

本文针对提出的层间过渡约束阻尼结构，建立其动力学方程，采用分布参数传递函数法导出解析解。并探讨过渡层参数行为对动力学特性的影响。

1动力学方程的建立

建立图2所示坐标系，假设粘弹阻尼层沿长度方向的拉伸应力是可以忽略的，其仅发生纯剪切变形；忽略基础层和最外约束层的剪切变形；同时略去各层之间的相对横向应变，即整个结构的侧向位移(坐标z的位移w)相等[11-12]。根据图2各层变形关系，可推得层间过渡阻尼结构振动时，过渡层的剪切角(ψ)与阻尼层的剪切角(γ)之间关系式如下：

(1)

式中：下标1、2、3、4分别表示基础层、过渡层、阻尼层和约束层；u表示各层的轴向变形分量；w为侧向位移；H表示各层的厚度。

图2　各层变形关系示意图Fig.2 Deformation pattern of each layer

对于阻尼层与过渡层，其剪切力可表示为：

τ3=G3γτ2=G2ψ

(2)

式中，G为剪切模量。

对于基础层、过渡层，其总的轴力(N12)、弯矩(M12)可分别表示如下

(3)

(4)

式中，(EA)表示轴向拉伸刚度，(EQ)表示各层弹性模量与面惯性矩的乘积，(EI)表示弯曲刚度。同理，对于约束层，有：

(5)

式中，E表示弹性拉伸模量，b为结构宽度。

考虑到整个阻尼结构受力平衡及根据牛顿第二定律，可得侧向(z向)平衡方程如下：

(6)

式中：ρ=∑ρi(i=1,2,3,4)，ρ为密度，q表示侧向外加载荷大小。

轴向(x向)平衡方程如下：

(7)

(8)

式中，f表示轴向拉力。

联立式(1)～(8)，得层间过渡约束阻尼结构动力学方程为：

(9)

式中,Dt=(EI)12+(EI)4；a=H1/2+H2+H3+H4/2

2分布参数传递函数解

定义层间过渡约束阻尼结构的状态向量：

对动力学方程(9)进行拉普拉斯变换，并表示成状态空间形式如下：

(10)

式中

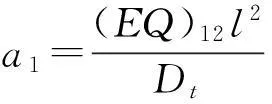
对于层间过渡约束阻尼结构，固定其基础层一端，并进行基础激振，其余附加层均为自由，其拉普拉斯域边界条件可改写为：

Mη(0，s)+Nη(l,s)=γ

(11)

式中，M和N表示边界条件选择矩阵；γ表示边界激振载荷向量。

根据分布参数传递函数方法[13]，方程(10)的解为：

(12)

式中，G(x,ζ,s)称为层间过渡阻尼结构域内传递函数矩阵，H(x,s)表示边界传递函数矩阵，分别为：

H(s)=eF(s)x(M(s)+N(s)eF(s))-1

求解特征方程：

det[M(s)+N(s)eF(s))]=0

(13)

即可获得层间过渡约束阻尼结构的复特征值si，进一步通过式(14)[11]即可得到结构的各阶固有频率fi及结构损耗因子ηi。

(14)

3算例验证

以层间过渡约束阻尼板为例，其几何参量为：长0.5 m, 宽0.3 m, 基础层厚H1=25 mm, 过渡层厚H2=20 mm，阻尼层厚H3=15 mm, 约束层厚H4=10 mm。材料参量为：基础层和约束层采用相同材料，其密度ρ1=ρ4=7 800 kg/m3, 拉伸模量E1=E4=2.1×1011Pa，泊松比ν1=ν4=0.3，过渡层密度ρ2=1 200 kg/m3，剪切模量G2=7.629×108Pa，泊松比ν2=0.45，阻尼层密度ρ3=1 130 kg/m3, 剪切模量G3=7.629×106(1+0.15i) Pa，泊松比ν3=0.499。

为了验证上述所建动力学模型及传递函数解的正确合理性，本文同时进行了有限元计算分析，获得层间过渡阻尼板的的前5阶固有频率和结构损耗因子，并与本文的解析解作比较，结果如表1所示。

表1　层间过渡约束阻尼板解析解与有限元结果比较

从表1可知，传递函数方法解析解与有限元计算结果基本一致，验证了本文解析法求解层间过渡阻尼结构动力学问题的正确性。但传递函数法求解计算量小，节省计算时间，相对有限元法具备一定的优势。

4分析讨论

4.1频响特性曲线讨论

图3　过渡层剪切模量和阻尼性能对频响特性的影响Fig.3 The effect of transition layer’s shear module and damping on frequency character

通过本文的传递函数法，还可对层间过渡约束阻尼结构的频响特性进行分析。在上节算例基础上，对阻尼结构基础层固定端处施加频率范围0～4 500的单位正弦激励，图3给出了过渡层剪切模量和阻尼性能对层间过渡约束阻尼板频响特性的影响。分析图3(a)可知，当过渡层剪切模量与阻尼层数量级相等时，此时，整个结构振动剧烈，欲获得良好的减振效果，只有提高过渡层的剪切模量实现。然而，对比图3(a)、(b)可知，若过渡层所选材料具有一定的内阻尼时，整个结构减振效果会得到一定的改进。另，从图3知，若过渡层与阻尼层材料相同时(点划线)，四层阻尼结构演变为传统的三层约束阻尼结构(等效为提高了阻尼层的厚度)，通常为了达到理想的减振要求，需增加阻尼层的厚度，然而随着阻尼层厚度的增加，结构损耗因子会达到一极限值，此时，即使再继续增加其厚度也不能够提高结构对振动能的损耗能力。经分析发现，当不改变阻尼结构厚度时，若让过渡层的剪切模量大于阻尼层(实线)，在结构振动时，过渡层可将变形传递给阻尼层，起到放大剪切变形的作用，从而消耗更多的振动能量。故 “层间过渡层”概念的引入，可提高结构的减振缓冲效果，且相对于多层(五层以上)结构，有着制作容易的特点。

4.2过渡层厚度的影响

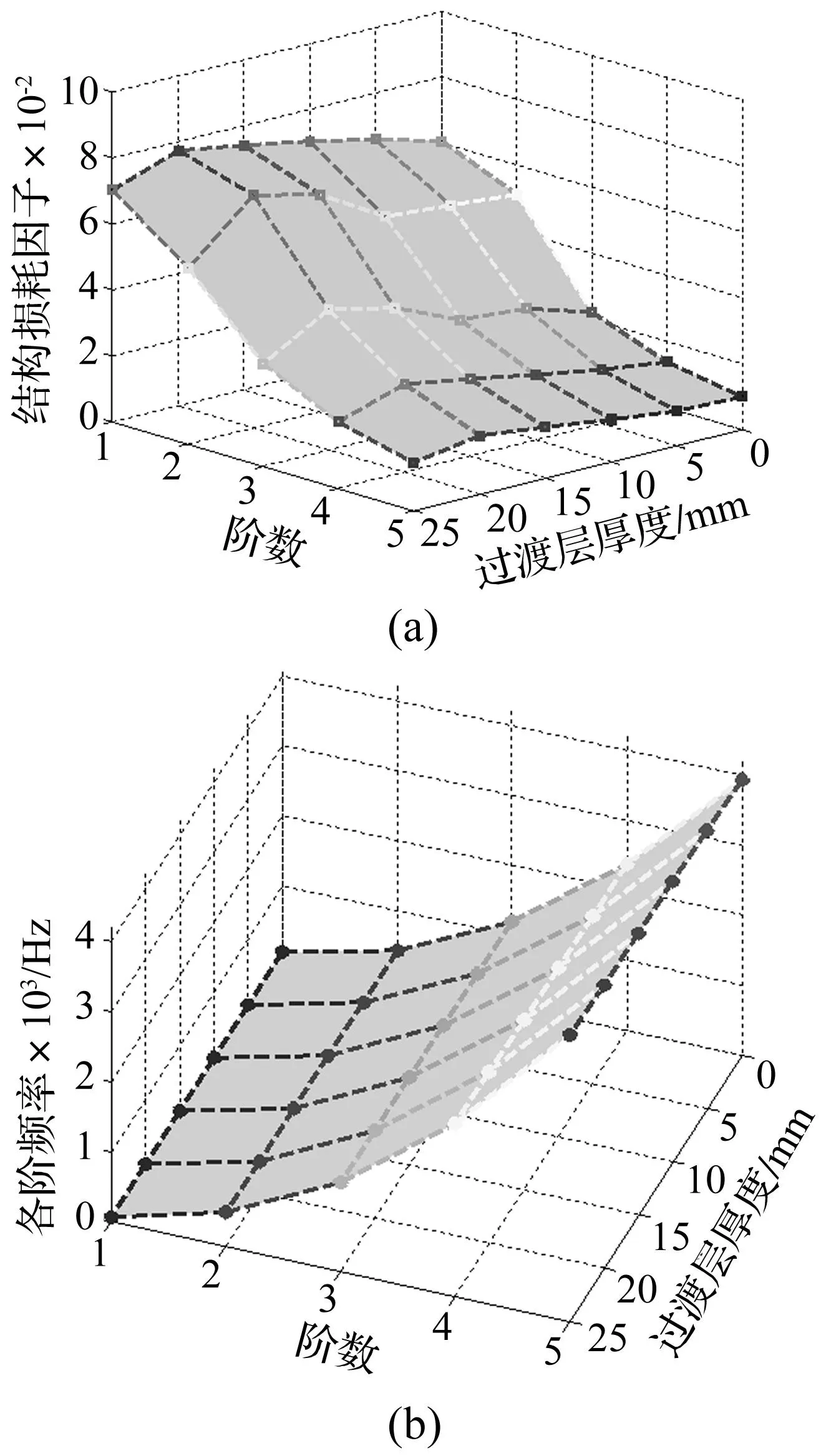
图4　过渡层厚度对损耗因子与频率的影响Fig.4 Influence of transition layer thickness on Loss factor and frequency

针对第3节算例，改变过渡层厚度，探讨阻尼板固有频率和结构损耗因子的变化趋势，其结果见图4。从图中可知，随着过渡层厚度的增加，结构刚度与质量均随之上升，但刚度增大对频率的影响相对于质量增大的影响更加显著，整个结构变“硬”，故阻尼板的各阶固有频率该条件下皆增大，但改变不明显。同时，随着过渡层厚度的增加，结构损耗因子并未持续增加，而在20 mm附近，存在最大值；另外经过分析发现，当过渡层厚度等于H2=0时，一阶损耗因子η1=0.060 7，H2=15 mm时，η1=0.074 1，H2=25 mm时,η1=0.070 4，故“过渡层”的引入，能够增加整个结构的能量耗散，但一味增加过渡层厚度并不一定能取得更好地放大阻尼层剪切变形效果。

4.3过渡层剪切模量的影响

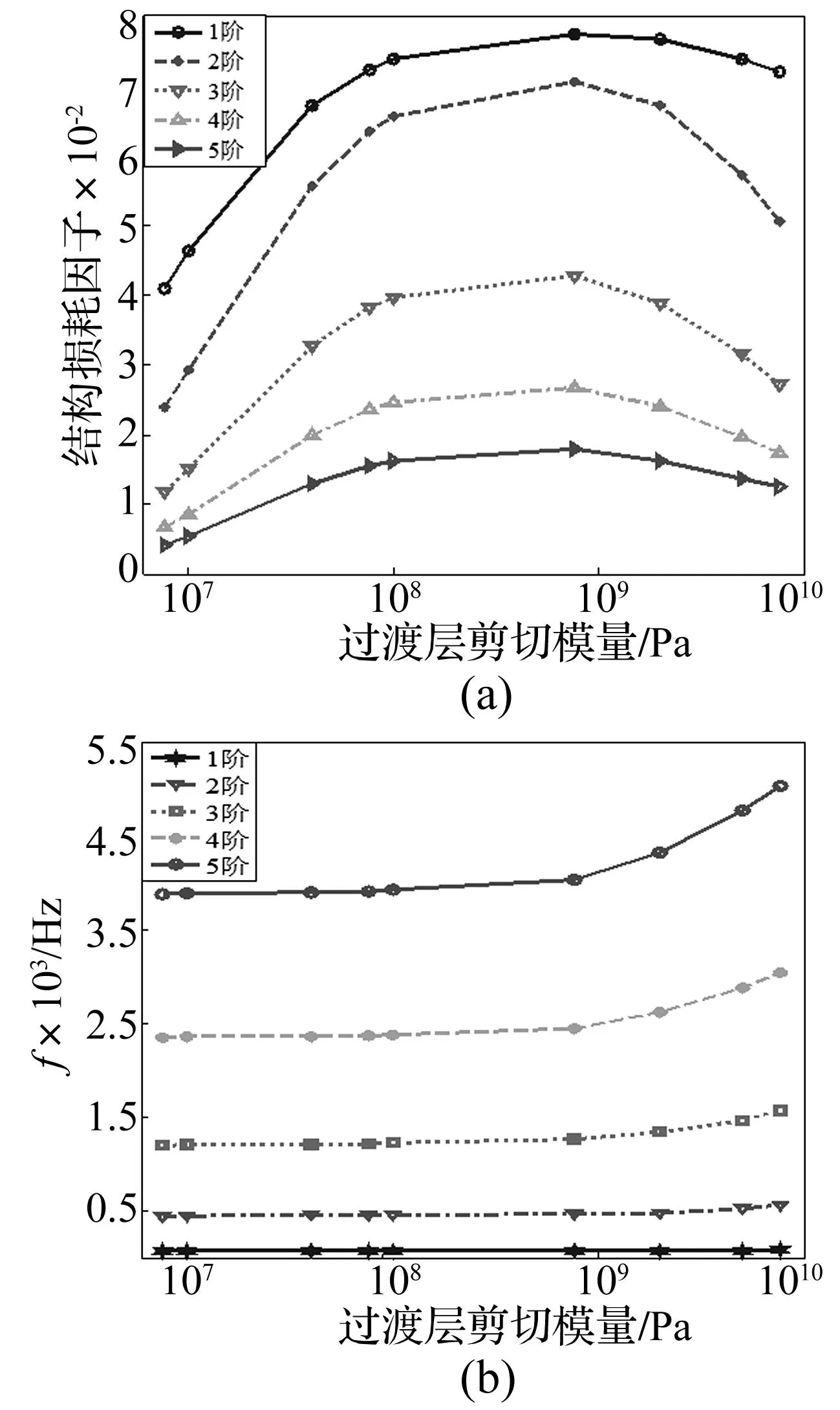
图5　过渡层剪切模量对损耗因子与频率的影响Fig.5 Influence of transition layer shear module on Loss factor and frequency

因过渡层的刚度低于阻尼层时，结构振动变形时，材料损耗因子较低的过渡层就将产生很大的动态应变，而不再起到扩大阻尼层变形的作用，故过渡层的剪切模量应具有某一合理的取值范围。图5给出了结构损耗因子及各阶频率随过渡层剪切模量变化情况。从图5(a)可知，在给定的剪切模量范围内(介于约束层金属材料和阻尼层黏弹性材料之间)，结构损耗因子存在峰值，从初始至当过渡层与阻尼层二者剪切模量相差2个数量级区间，曲线上升明显，随后变化较平缓，而当过渡层剪切模量接近约束层时，损耗因子又有所下降。同时，分析图5(b)频率变化趋势可知，各阶均随着过渡层剪切模量增加而逐渐上升，当G2=7.629×109Pa时，第五阶变化最为明显，而其它各阶(特别是第一阶)改变不太明显。另对于第一阶，当G2=7.629×106Pa时，f1=68.250 Hz;G2=1×107Pa时，f1=68.401 Hz;G2=7.629×108Pa时，f1=73.075 Hz;G2=7.629×109Pa时，f1=76.967 Hz。

4.4过渡层密度的影响

表2给出了各阶频率及结构损耗因子随过渡层密度变化情况。从中可知：当层间过渡约束阻尼结构的其它参数固定时，其各阶固有频率及第一阶损耗因子均随着过渡层密度的增大而减小；而其余各阶损耗因子则随着过渡层密度的增大而增大，但整个结构阻尼损耗因子的变化并不明显。

4.5过渡层泊松比的影响

在层间过渡约束阻尼结构其余参数保持恒定的情况下，改变过渡层材料的泊松比，探讨结构的动力学特性。其各阶频率及损耗因子随过渡层泊松比的变化情况见表3。经分析发现，随着过渡层泊松比的增加，整个结构的弯曲刚度随之增加，故各阶固有频率也略有增加，但影响不是很大。同时，当过渡层材料泊松比在0.3～0.499范围内变化时，各阶损耗因子几乎未发生改变，故改变材料泊松比对提高整个结构损耗因子的贡献甚微。

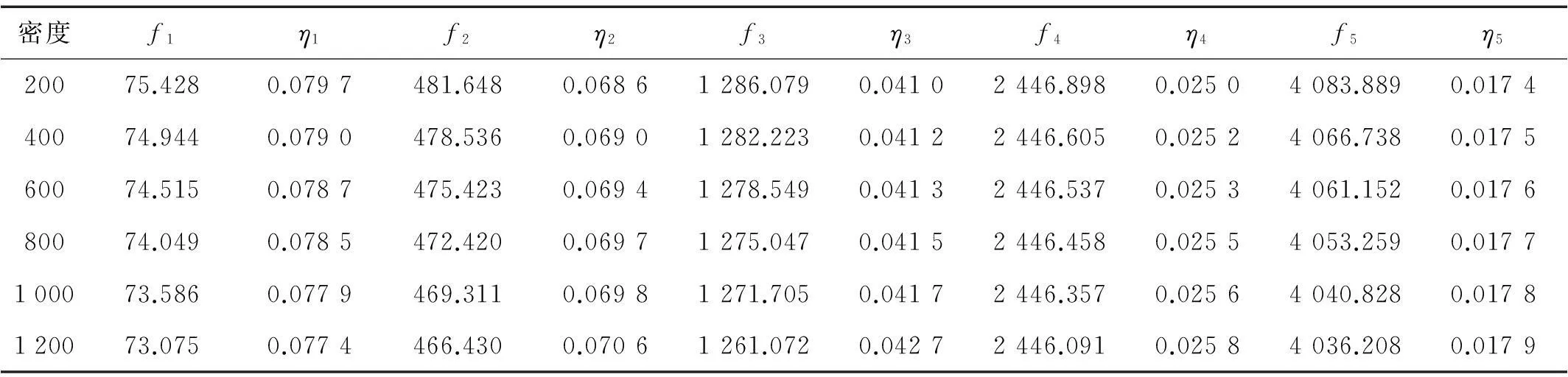
表2　过渡层密度(单位：kg/m3)对各阶固有频率(单位：Hz)及损耗因子的影响

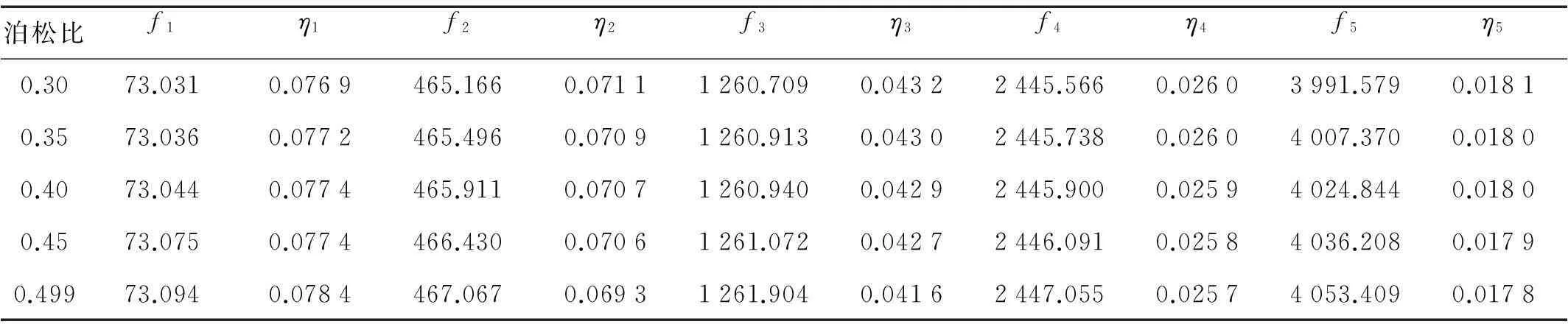
表3　过渡层泊松比对各阶固有频率(单位：Hz)及结构损耗因子的影响

5结论

(1) 本文引入“层间过渡层”设计的概念，提出了一种层间过渡约束阻尼结构，经推导，建立了其动力学方程，给出了其分布参数传递函数解析解。经与有限元计算结果对比，验证了该方法的正确性。

(2) 传递函数法可分析层间过渡约束阻尼结构的频响特性，经探讨得知，过渡层的引入，能起到放大阻尼层剪切变形的效果，增加结构的能量耗散，且过渡层具有内阻尼时，减振效果更佳。

(3) 过渡层参数行为对阻尼结构动力学特性有着重要影响。经分析知，过渡层厚度与剪切模量对整个结构动力学特性影响明显，而其密度及泊松比影响不大，故在实际应用中，过渡层厚度及剪切模量的选取相对泊松比、密度的选取更为重要。随着过渡层厚度和剪切模量在一定范围内增加，结构的各阶固有频率逐渐上升；而损耗因子存在峰值。本文分析理论及结果为进一步优化工作打下了良好基础。

参 考 文 献

[ 1 ] Zheng W G, Lei Y F, Li S D. Topology optimization of passive constrained layer damping with partial coverage on plate[J].Shock and Vibration,2013, 20(2):199-211.

[ 2 ] 舒歌群, 赵文龙, 梁兴雨,等. 约束阻尼结构的振动分析及结构参数优化研究[J]. 西安交通大学学报,2014, 48(3):108-114.

SHU Ge-qun, ZHAO Wen-long ,LIANG Xing-yu, et al. Vibration analysis and optimization of composite sStructure with constrained-layer damping treatment[J]. Journal of Xi’an Jiaotong University, 2014, 48(3):108-114.

[ 3 ] Kumar S, Kumar R. Theoretical and experimental vibration analysis of rotating beams with combined ACLD and Stressed Layer Damping treatment[J]. Applied Acoustics, 2013, 74(5):675-693.

[ 4 ] Lepoittevin G, Kress G. Optimization of segmented constraining layer damping with mathematical programming using strain energy analysis and modal data[J]. Material Design, 2010,31(1):14-24.

[ 5 ] Gao J X, Liao W H. Vibration analysis of simply supported beams with enhanced self-sensing active constrained layer damping treatments[J]. Journal of Sound and Vibration.2005, 280(1/2):329-357.

[ 6 ] Sun Da-gang, Zhang Xin, Song Yong, et al. Optimization for sandwich damping composite structure used in sprocket of crawler vehicles[J]. Sandwich Structures and Materials,2012,14(1):95-110.

[ 7 ] 李恩奇, 唐国金, 雷勇军,等. 约束层阻尼板动力学问题的传递函数解[J]. 国防科技大学学报, 2008,30(1):5-9.

LI En-qi, TANG Guo- jin, LEI Yong-jun, et al. Dynamic analysis of constrained layer damping plate by the transfer function method[J]. Journal of National University of Defense Technology, 2008,30(1):5-9.

[ 8 ] 杨坤, 梅志远 , 李华东. 复合材料夹层梁动力响应的传递函数法求解[J]. 华中科技大学学报：自然科学版, 2013, 41(5):39-44.

YANG Kun, MEI Zhi-yuan, LI Hua-dong.Solving dynamic response for composite sandwich beams by transfer function method[J].Journal of Huazhong University of Science and Technology: Nature Science,2013, 41(5):39-44.

[ 9 ] Yang B, Tan C A. Transfer function of one-dimension distributed Parameter system[J]. ASME Journal of Applied Mechanies, 1992, 59(4):1009-1014.

[10] Susanto K S．Design, modeling and analysis of piezoelectric forceps actuator[D]. Los Angeles: Department of Mechanical Engineering, University of Southern California, 2007．

[11] 李恩奇, 雷勇军, 唐国金,等. 基于传递函数方法的约束层阻尼梁动力学分析[J]. 振动与冲击，2007,26(2):75-78.

LI En-qi, LEI Yong-jun, TANG Guo-jin, et al. Dynamic analysis of a constrained layer damping beam by transfer function method[J]. Journal of Vibration and Shock, 2007, 26(2):75-78.

[12] Yellin J M, Shen I Y, Reinhall P G, et al. An analytical and experimental analysis for a one-dimensional passive stand-off layer damping treatment[J].ASME Journal of Vibration and Acoustics, 2000,122: 440-447.

[13] 周建平，雷勇军.分布参数系统的传递函数方法[M].北京：科学出版社，2010.

Distributed parameter transfer function method for dynamic response of a constrained damping structure with transition layer

YANBi-juan,ZHANGWen-jun,LIZhan-long,SUNDa-gang(Mechanical Engineering College, Taiyuan University of Science and Technology, Taiyuan 030024, China)

Abstract:To solve limited vibration energy consumption problems of a traditional constrained damping structure, the concept of “transition layer” was introduced and a type of constrained damping structure with transition layer was proposed. The dynamic response for this damping structure was analyzed with the distributed parameter transfer function method. The analytical solutions of structural loss factor and frequency for a cantilevered damping plate were deduced, and a finite element simulation was also done. The calculation results of both two methods agreed well each other. The effects of transition layer’s parameters behavior on the cantilevered damping plate’s frequency response characteristics were analyzed. The results showed that the transition layer can transfer deformation to the damping layer and enlarge the shear deformation of the damping layer, so more vibration energy was dissipated when the structure vibrates. At the same time, the effects of thickness, shear modulus, density and Poisson ratio of the transition layer on structural natural frequencies and loss factors were also discussed. The results laid a good foundation for the further optimization.

Key words:transfer function method; transition layer; constrained damping; dynamic response

中图分类号:S219.032.2

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.05.030

收稿日期：2014-12-30修改稿收到日期：2015-03-17

基金项目：国家自然科学基金(51405323;51305288)；太原科技大学博士启动基金(20132002)

第一作者 燕碧娟 女，博士，副教授，1975年生