巧用“几何平均值”求解 “与距离平方成反比”的力做功

程 柏

(新疆生产建设兵团第七师高级中学　新疆 伊犁　833200)



巧用“几何平均值”求解 “与距离平方成反比”的力做功

程 柏

(新疆生产建设兵团第七师高级中学新疆 伊犁833200)

摘 要：万有引力与库仑力是高一、高二学生在学习物理时所遇到的两种大小与距离平方成反比的力，求解这种变力做功，是深刻认识这两种场力，进一步体会保守力场势能概念的重要过程.然而此阶段的高中生并未学习到微积分这一数学工具，如果只是简单地告知引力势能或两个点电荷间的电势能的表达式，这对于学有余力的优等生在概念建构上是不利的.为避免教师“想讲清楚，但讲不清楚”的尴尬境地，可采用初等数学的“几何平均值”法来求解这种变力的功.

关键词：几何平均值万有引力库仑力功

1万有引力的功与引力势能

如图1所示，以地心为坐标原点，沿地球半径方向建立x轴.

图1

设地球质量为M，当质量为m的物体从距离地心r2处沿x轴移到距离地心r1处过程中，引力做的功可以这样计算：把r1到r2的距离分成无限多个小段，取其中第n小段，从与地心距离rn+1到rn，Δrn=rn+1-rn为一小量，在该区间内引力近似为一常量，有

(Δrn)2为高阶小量，微乎其微，忽略不计，上式简化为

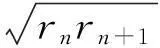
具有承上启下的意义，正是可作为第n小段的几何平均恒力来求此段“平方反比”变力的功.

这个过程万有引力的功为

则物体从r2处移到r1处过程中，引力的总功为

-ΔEp=ΔEk=W

一般地，常把物体在无穷远处(r2→)时的势能看作零势能点(Ep2=0)，则对于上式可知物体位于距地球球心O点为r(r=r1)处时的引力势能为

为物体和地球系统共同具有.

2库仑电场力的功与两个点电荷系的电势能

由于所有带电体的电场均可以等效视为一系列点电荷电场的叠加，故研究点电荷库仑电场力做功就具有很重要的意义.

如图2所示，在O点固定一个电荷量为+Q的点电荷，另一个带电量为+q的点电荷位于距离O为ra的a点，沿任意路径运动到距离O为rb的b点，如何计算库仑电场力的功呢？

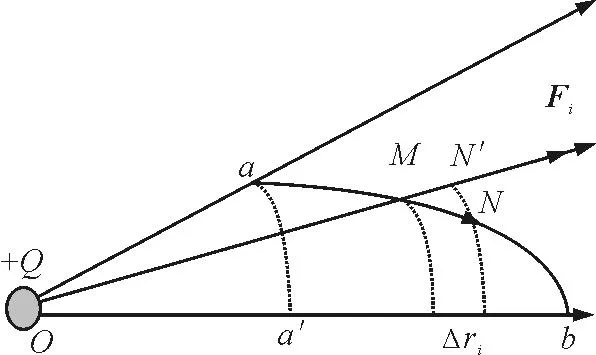
图2

将时间(或空间)分成无数小段, 便可“以恒代变”“以直代曲”， 然后累积取舍， 使之向真实情况无限趋近.这是物理学中常用的一种处理类似于上述复杂问题行之有效的思维方法.基于这种思维方法,我们将运动路径分割成无数个有限小段.每一小段即可看成是恒力作用下的运动，进而求这一小段的功.

取任意小段MN，设其位移为Δli，点电荷在M点所受的电场力为Fi，电场力在这一小段位移的功为

ΔWi=FiΔlicosθi

式中θi为位移Δli与电场力Fi的夹角.

以O为圆心，ON为半径作一圆弧，交过M的电场线于N′点，当MN′很小时，则可认为MN′=Δlicosθi.再以O为圆心，分别作OM，ON为半径的圆弧，使它们和Ob电场线相交，可以在Ob线上得到一小线段Δri=Δr=ri+1-ri，其大小和MN′相等，在这小段Δri上做库仑力的几何平均值处理，有

根据点电荷电场的对称性可知，试探电荷从M移动到N过程中电场力所做的功与试探电荷沿电场线Ob移动Δri所做的功相等.

以此类推，可把点电荷+q沿任意路径每一小段电场力的功都等同到同一电场线Ob上各相应小段电场力的功，这样，电荷沿任意路径从a移动到b时，都等同于从a′移动到b所做的功.可表示为

Epa-Epb=-ΔEp=

选取无穷远处(rb→)为零电势能点，则电荷q距离场源电荷Q为r处的a点(ra=r)电势能即

3教学启示

应当重视“微元法”的显化，高中生即将进入大学深造，抽象思维开始快速发展，面对难以解决的问题需要新的思维方法，这就要求教师抓住机会向学生显化物理本质.继探究重力势能、弹簧变力功下的弹性势能后，对于学优生来说，掌握“平方反比”变力的功，探究引力势能和库仑场的电势能，对于深刻理解保守力场势能的概念很有好处，对促进学生运用数学知识解决物理问题的能力方面大有裨益！

(收稿日期：2015-11-17)