极坐标系在大学物理中的应用探析*

吴 杰

*教育部高等学校大学物理课程教指委教学研究立项项目,项目编号： DWJZW201533zn



极坐标系在大学物理中的应用探析*

吴 杰

*教育部高等学校大学物理课程教指委教学研究立项项目,项目编号：DWJZW201533zn

摘 要：举例介绍了极坐标系在力学和电磁学中的应用.指出在求解大学物理问题中,通过选用适当的坐标系可以优化物理模型,简化计算过程,从而提高学生的学习兴趣和积极性.

关键词：极坐标系力学 电磁学毕奥-萨伐尔定律

大学物理中引入了矢量和微积分的知识之后,对各个物理量的定义相对于中学物理更具有普遍性,各种定理、定律的适用范围更广泛.但是要对一个物理量进行具体的描述,仍需要确定其大小和方向,这就需要坐标系来给出标准.最常用的坐标系有直角坐标系、自然坐标系、极坐标系及球坐标系等.在现行的大学物理教材中,对于一维直线运动或者抛物线运动通常采用的是直角坐标系,一般曲线运动中用的是自然坐标系[1,2].实际上,在极坐标系中,由于点的极坐标有着十分明显的物理意义,在解决问题过程中,合理应用其物理意义,不仅可以比较容易地找出研究对象,简化解题步骤,提高解决问题的能力和速度,更重要的是可以克服学生学习物理的畏惧心理,增强自信心,为后续课程的开设打下基础.

1极坐标系及运动学表示

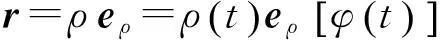
图1　极坐标系

这两个单位矢量和直角坐标系中单位矢量之间的转化关系为

(1)

两边同时求导可得

(2)

注意：牢记式(2)这两个微分关系能解决大学物理中的很多问题.

质点位移的表示为

dr=dρeρ+ρdφeφ

(3)

质点速度的表示

上式就是加速度a在极坐标系中(用eρ,eφ展开)的表示,其中加速度的径向分量aρ(径向加速度分量)和横向分量aφ(横向加速度分量)分别为

在圆周运动中由于径向坐标等于常数,所以

2应用举例

2.1极坐标在力学中的应用

图2　引力做功

【例1】卫星绕地球运动引力做功问题.假设地球质量M,卫星质量为m,地球固定不动,卫星在地球引力作用下,从A点沿任意路径运动到了B点,讨论整个过程中地球引力对卫星所做功.

解析：以力心M为极点, (ρ,φ)为极坐标, 建立极坐标系.

由式(3)可得出

在现行的大学物理教材中,对于万有引力及库仑力做功,通常采用近似的方法,而实际画图都不可能真实描绘出真正的运动,所以学生在判断时很难有两个底角都是直角的三角形这个概念.虽然保守力做功特点记住了,但真正的原因还是没有明白.引入极坐标系之后,只需按照功的概念,代入公式正常求解便能得出简化的结果.

【例2】质量为m,长为l的均匀细棒,可绕垂直于棒的一端的水平轴自由转动,如图3所示,将此棒的自由端放在水平位置,然后放开任其落下,求棒转过φ0角时水平轴的支持力N.

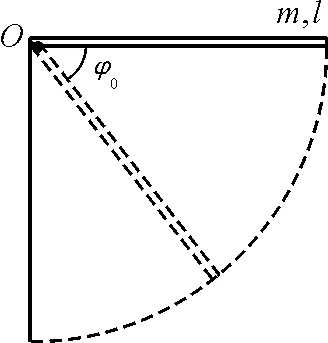
图3　例2用图

解析：在讲到刚体力学部分,经常涉及到子弹与杆的碰撞问题,由于思维定势,学生常常利用动量守恒来解决问题,因为求解的复杂性,教师也很少去分析受力情况,只是定性的说明而没有定量的求解,会使学生理解不深,从而持有怀疑态度.如果用极坐标系与简单的刚体内容,此问题便会迎刃而解.

如图所示取O点为极点,水平为极轴方向,棒的方向为径向.由动能定理可知,细棒转过φ角时的角速度、角加速度分别为

棒的动量为

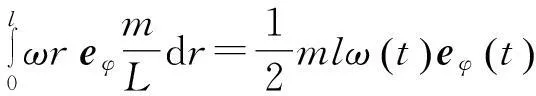
(4)

对该时刻应用质点系的动量定理,并利用式(2)可得

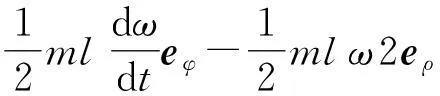
(5)

所以

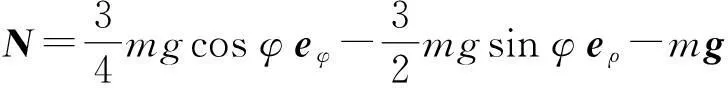
(6)

若另取水平方向为x轴,垂直向上为y轴的直角坐标系xOy,则有

(7)

将式(7)代入式(6)得

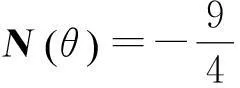
(8)

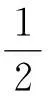
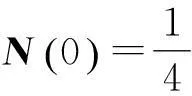
大小变为原来的一半,当棒摆至最低端时

在力学中的很多实际问题中如果采用极坐标系, 并且利用径向速度与横向速度的概念, 不仅可以简化物理模型,方便地解决此问题, 而且物理图像特别清晰.

2.2极坐标在电磁学中的应用

图4　极坐标系下的毕奥- 萨伐尔定律

利用极坐标可以简化平面电流的毕奥-萨伐尔定律.如图4所示，在导线上取一电流元,并以场点为极点O,建立平面极坐标系.ρ为极点到电流元的矢径,水平向右为极轴,φ为极角,则有

在这里由式(3)可得

在极坐标系中,ρ是极角的函数,即ρ=ρ(φ), eφ与eρ属于正交关系,可以由右手螺旋关系判断B的方向,如果所有电流元电流方向一致,B的方向为垂直于电流与场点组成的平面,并满足右手螺旋关系. 由此可得出整个平面电流在场点激发的磁场大小为

(9)

此式就是毕奥-萨伐尔定律在极坐标系中的表达式,原则上可以根据该式计算任意一个平面载流线圈在某点激发的磁场[4,5].

【例3】在真空中有一通有电流I的长直导线,求此长直导线附近任意一点P处的磁感强度.已知任意一点P到长直导线的垂直距离为r0.

图5　载流直导线的磁场

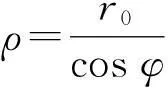
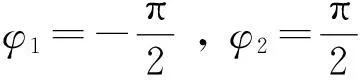
利用极坐标系下的毕奥-萨伐尔定律还可以求物线形、椭圆形状的载流导线焦点处的磁场,和直角坐标系相比,简化了计算过程,并可以扩展到载流二次曲线的磁场分布[6～9].由于篇幅所限,这里不再赘述.

3结论

通过以上关于极坐标系在力学、电磁学中的应用讨论可以看出：对于同一个物理问题来说,参照系的选择原则上是任意的,但参照系的不同对问题研究的难易程度有很大的影响,具体表现为模型建立的简易、计算上的冗简.很多学生因为惧怕数学而放弃物理,所以优化模型、简化计算过程是大学物理教学中应该重视的一个方面. 直角坐标系中横坐标与纵坐标实质是用垂直的分向量来表示点的位置;极坐标系中的极径与极角实质是用长度和角度来表示点的方位,涉及距离或角的问题简捷明快.在研究具体问题时,应遵循简单、方便、可行的原则,建立适当的坐标系,优化解题路径,提高学生的解题能力,从而培养他们学习物理的兴趣,增加自信心！

参 考 文 献

1马文蔚. 物理学教程.北京：高等教育出版社, 2006

2毛骏健. 大学物理学. 北京：高等教育出版社, 2006

3周衍柏. 理论力学教程. 北京：高等教育出版社, 1986

4王历. B-S定律的极坐标形成及其应用. 长江工程职业技术学院学报, 1992,4(4):28～31

5殷岳才, 陆莲芳. 毕奥-萨伐尔定律在极坐标系中的表达式及其应用. 沈阳师范大学学报：自然科学版, 1996,14(2):21～24

6王琪. 二维光滑曲线约束力的一般计算方法. 大学物理, 1993,12(7) :21～23

7袁泉, 赵力成, 李久会. 椭圆电流焦点处磁场计算. 渤海大学学报：自然科学版, 2006, 27(2):149～150

8林乐鑫, 肖化, 周少娜,等. 抛物线电流对称轴任意点磁场的理论计算和实验验证. 大学物理, 2014, 33(4):11～14

9卢芳, 成泰民, 王金刚. 圆锥曲线电流在焦点处的磁感应强度. 物理与工程, 2007, 17(2):36～38

Analysis on Application of the Polar Coordinate System in University Physics

Wu Jie

(The School of Physics and Electronic Engineering, Zhengzhou University of Light Industry, Zhengzhou，Henan450002)

Abstract:This paper illustrates the application of polar coordinate system in mechanics and electromagnetism. It was pointed out that the physical model can be optimized and the calculation process can be simplified by choosing the appropriate coordinate system,thus The interesting and enthusiasm of students in physics are improved.

Key words:polar coordinate system; mechanics; electromagnetism; Biot-Savart Law

(收稿日期：2015-11-26)

*作者简介：吴杰(1977-),女,硕士,讲师,研究方向为粒子与原子核物理.
(郑州轻工业学院物理与电子工程学院河南 郑州450002)