一种改进的TOPSIS算法及其在贵阳市水质评价中的应用研究
2016-04-18吕亚楠吴有富杨正云贵州民族大学理学院贵州贵阳550025
吕亚楠,吴有富,杨正云(贵州民族大学理学院,贵州贵阳550025)
一种改进的TOPSIS算法及其在贵阳市水质评价中的应用研究
吕亚楠,吴有富,杨正云
(贵州民族大学理学院,贵州贵阳550025)
摘要:针对TOPSIS法在进行综合评价时相对贴进度算法存在的缺陷,作者提出了相对贴近度算法的改进方法;并将AHP和熵权法计算得到的组合权作为各评价指标的权重以避免权重确定的主观性和单一性。作者建立了组合权和改进的TOPSIS方法相融合的水质评价模型,并将其应用于贵阳市的水质评价,仿真结果表明此方法具有较强的有效性和可行性。
关键词:水质评价;TOPSIS法;熵权法
水质评价是水环境质量评价的重要内容之一,然而水质评价仅对水的各单项指标进行分析,往往会使评价结果与实际情况不相符,甚至可能得出错误的结论。基于此,国内外学者相继提出了综合指数法、层次分析法、灰色关联度法、人工神经网络法以及模糊综合评价法等水质评价方法[1-3]。这些方法各有优缺点,例如综合指数法和层次分析法(AHP)简单实用,但主观性太强;模糊综合评价法虽然考虑了水质分级界限的模糊性,但隶属度函数的构造存在一定难度。运用这些方法进行水质评价时,关键是确定指标的权重。AHP法是目前广泛应用的一种确定指标权重的方法,计算简单,思路清晰,但主观性太强。作者引入AHP-熵权法对评价指标的权重进行组合赋权,避免了赋权的主观性和单一性,同时作者将改进的TOPSIS模型应用于贵阳市的水质综合评价,通过与其他方法进行对比证明了该方法的有效性和可行性。
1 TOPSIS综合评价方法
TOPSIS法[4]即逼近理想解排序法,其核心思想是通过对比评价方案与最优方案和最劣方案之间的距离来评价方案的好坏程度。与正理想解的距离越近(即最优方案的距离),评价结果就越好,反之也然。其建模过程如下。
(1)决策矩阵
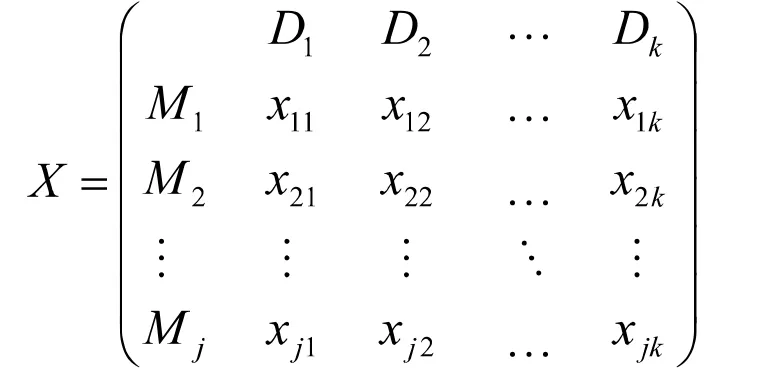
(2)无量纲化矩阵
为了消除数据量纲的影响,通过下面的方法来对数据进行无量纲化处理,使原始数据区间化为[0~1]之间,最后形成归一化矩阵公式如下:
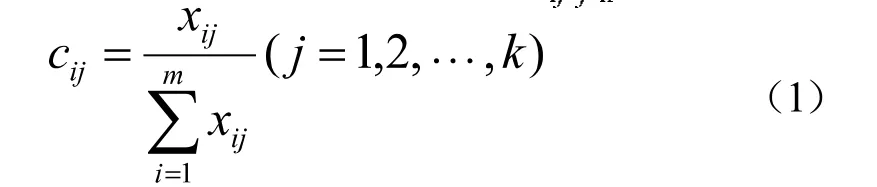
(4)理想解
正理想解:

负理想解:
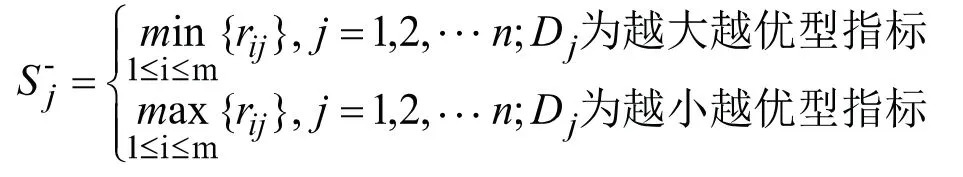
计算每种方案与正负理想解之间的欧式距离,公式如下:
与正理想解距离
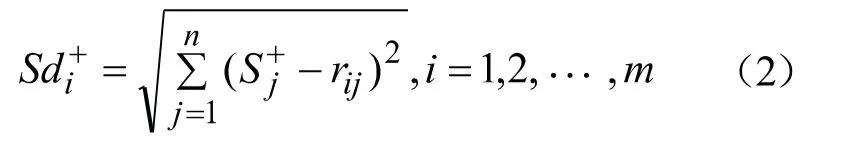
与负理想解距离
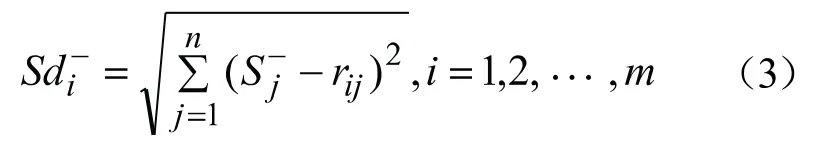

(6)改进的相对贴近算法
由于公式(4)是利用各方案与正负理想解的欧式距离比来衡量各方案的好坏,而实际情况下某一方案可能同时离最优解和最劣解都很近或者都很远,因此考虑公式,并弱化的作用,同时避免分母为0,将公式(4)做如下改进:越接近
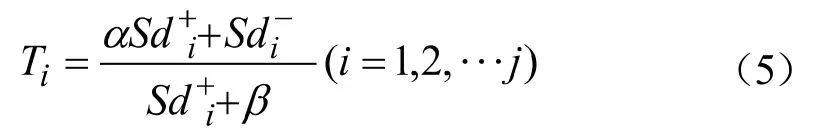
2指标权重的确定
2.1层次分析法确定指标权重
层次分析法[5]是通过数学方法对多目标决策问题进行定性和定量分析,将复杂的系统划分为相联系的递阶型层次结构;通过专家对客观事实给出的相对重要度,构造判断矩阵,确定每一层次相对重要性的单排序;最后利用数学方法进行综合判断,得出全部指标相对重要性总排序的权重系数。建模过程一般有:通过专家经验构造判断求解判断矩阵的最大特征值及其对应的特征向量;对判断矩阵进行一致性检验是否当判断矩阵符合一致性检验时,求出权重排序向量。
2.2熵权法
熵权法[6]是根据各个评价指标所提供的有效信息量对其进行客观赋权的方法,在评价过程中,熵值的大小主要取决于评价指标值的变异程度。评价指标值的变异程度越大,熵值就越小,权重越大;反之,熵值越大,权重越小。因此可根据各个评价指标值的变异程度,利用熵值来确定各指标的权重。计算步骤如下。
(1)原始指标数据无量纲处理
根据公式(1)的方法对原始数据进行无量纲化处理,得到归一化的数值ij。
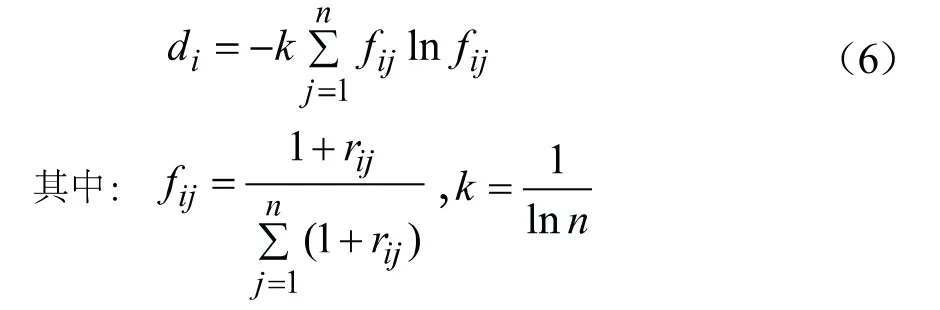
(3)计算第i项指标的熵权,公式如下:

2.3组合赋权
评价指标权重是评价指标相对重要性的定量表示,指标权重好坏直接影响综合评价结果的准确性。在权重赋值方法中,层次分析法能通过构建判断矩阵对评价指标进行定量分析,但主观性太强;熵权法能反映指标信息熵的有效价值,从数据本身出发,客观赋权,所得的权重更具可信度,但忽略了主要因子的影响。由于单一的权重赋值法存在一定的片面性,因此作者采用层次分析法和熵权法两种方法融合,将两种方法的优势进行互补,运用简单的算术平均法进行权重的组合,如下式:

3实例分析
作者以贵阳市南明河城区地下水水质资料为例[7],共设5个取样断面,每个取样断面测量水的pH值,溶解氧(DO)、五日生化需氧量及氨氮四项评价指标。各指标测量结果见表1。
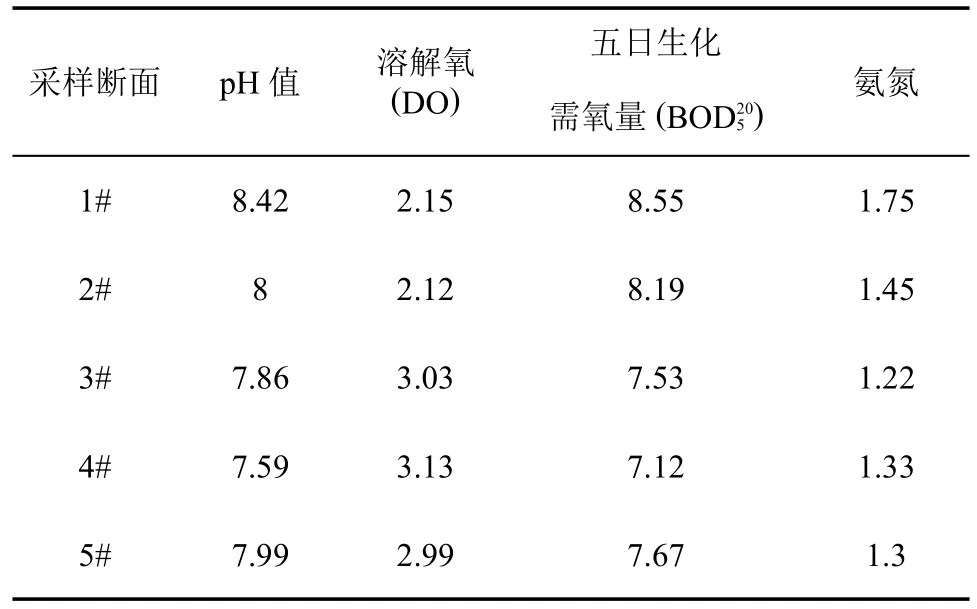
表1各采样断面评价指标实测值(mg/L)
根据地表水环境质量标准(GB3838-2002),依据地表水环境功能和保护目标,按功能高低依次划分为5类,见表2。
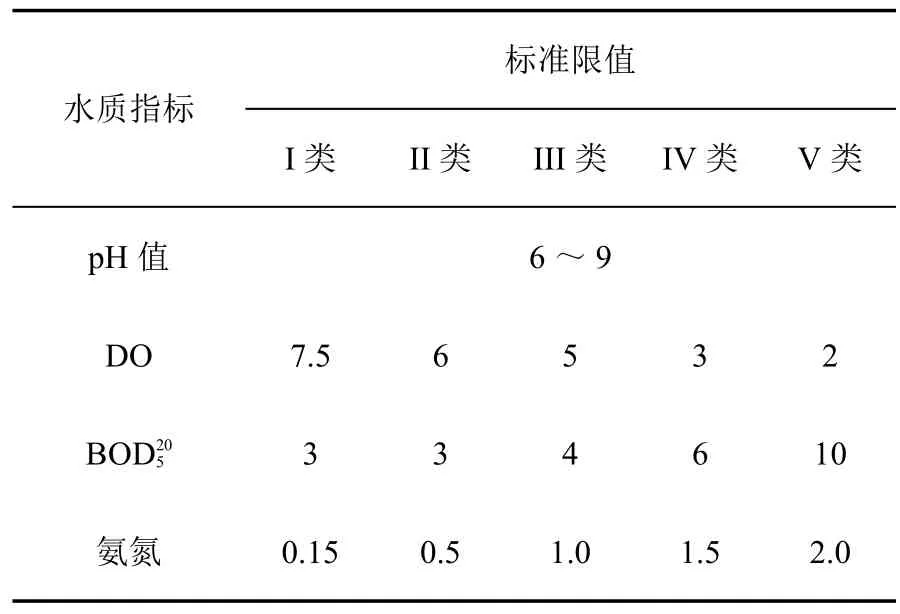
表2水质污染分级标准(mg/L)
将表2中III类、IV类、V类水质污染标准分界值作为判别样品与表1的数据一起形成增广型矩阵
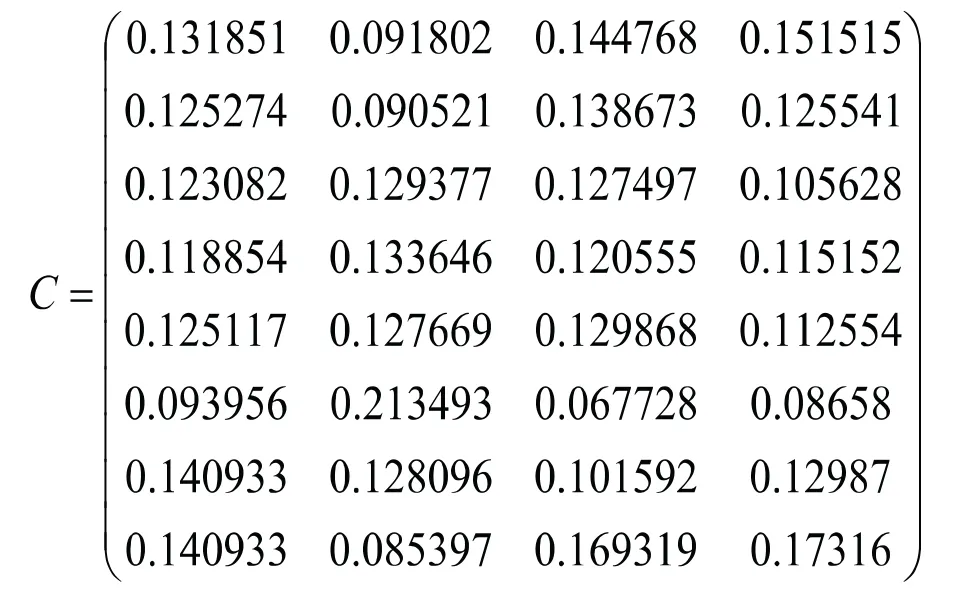
根据层次分析法原理,利用Matlab软件进行算法实现,求出各指标权重向量=(0.1131 0.2033 0.2769 0.4067);同理,运用熵权法按照公式计算,得到各评价指标的权重向量=(0.2498 0.2503 0.2498 0.2501);通过公式(8),可以得到指标的组合权重=(0.1815 0.2268 0.2633 0.3284)。
运用改进的TOPSIS综合评价,结果如下:
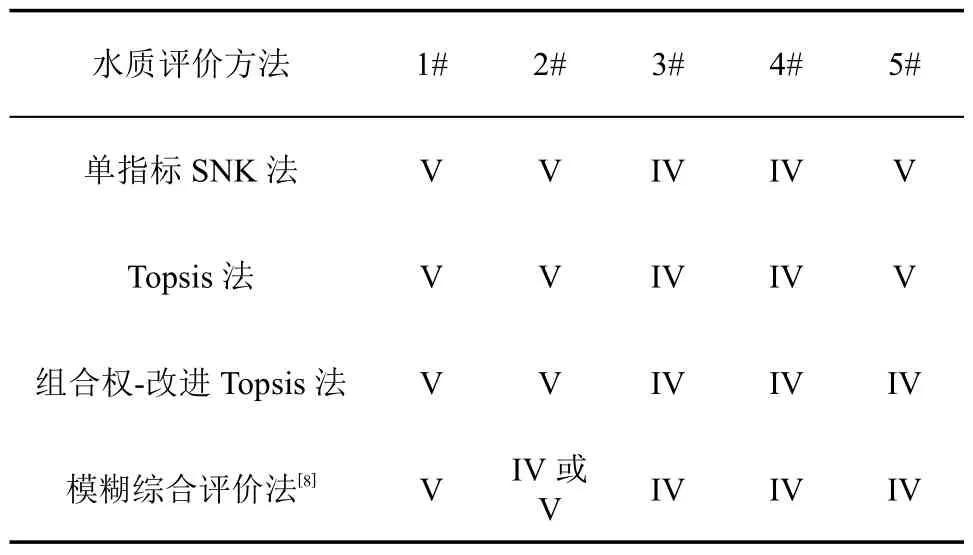
表3几种方法评价结果比较
通过对贵阳地下水水质的综合评价可知:层次分析法注重最大污染指标的影响,确定主要污染物为氨氮,其权重系数为0.4067,忽略了其他指标的作用,使得权重赋值过于偏重;在评价过程中由于传统TOPSIS综合评价法的贴近度算法存在问题,导致对水质等级产生错误判断,得出的5#水质等级为Ⅴ级,评价结果较为保守。而通过改进的TOPSIS综合评价法,权重赋值利用层次分析法考虑了最大污染指标的影响,同时利用熵权法对其进行修正,使得指标权重系数更符合水质的实际情况。采用改进的贴近度算法,弥补了传统贴近度算法的缺陷,得出5#水质等级为IV级,使评价结果更为准确。改进的TOPSIS综合评价法的评价结果与模糊综合评价模型的评价结果具有较好的一致性,比传统方法更能准确反映地下水的水质状况,评价结果更为合理。
4结论与展望
作者将改进的TOPSIS法应用于贵阳市的水质综合评价,评价结果更为客观、准确。与传统的TOPSIS方法和模糊综合评价法比较,其优点在于:(1)作者采用AHP-熵权法组合赋权,能利用两种方法的优势进行互补,综合考虑了指标的主观性和差异性的影响,使权重赋值更符合地下水水质的实际情况;(2)传统的TOPSIS评价法利用各方案同时与最优解和最差解的距离比作为评判原则来衡量方案的好坏,使最终的评价结果存在误差,影响评价的准确性,不能准确反映水质的类别。改进的贴近度算法弱化了的影响,使评价数据更为精确,评价结果更符合实际情况,通过与模糊综合评价法进行比较,验证了改进方法的有效性、合理性。
从表3可以看出,改进的TOPSIS综合评价法的评价结果与模糊综合评价模型的评价结果具有较好的一致性,而模糊综合评价将2#定为IV或者V级,是因为模糊综合法的权重赋值主观性和隶属度函数的差异所致;由于模糊综合法隶属度函数的构造存在主观性且计算复杂,在方法的实用性上,改进的TOPSIS评价法更优。
参考文献:
[1]郭显光.改进的熵值法及其在经济效益评价中的应用[J].系统工程理论与实践,1998,(12):99-103.
[2]张先起,梁川,刘慧卿.基于熵权的改进TOPSIS法在水质评价中的应用[J].哈尔滨工业大学学报,2007,(10):1670-1672.
[3]杨建仁,刘卫东.基于灰色关联分析和层次分析法的新型工业化水平综合评价——以中部六省为例[J].数学的实践与认识,2011,(2):122-132.
[4]肖淳,邵东国,杨丰顺.基于改进TOPSIS法的流域初始水权分配模型[J].武汉大学学报(工学版),2012,(3):329-334.
[5]张雯婷.长江经济带中心城市低碳经济综合评价研究[D].武汉:武汉理工大学,2013.
[6]陈启明,陈华友.改进的熵值法在确定组合预测权系数中的应用[J].统计与决策,2011,(13):159-160.
[7]谢春,周婕,张华.南明河贵阳城区段不同断面水质分析[J].贵阳医学院学报,2011,(2):165-167.
[8]杨静.改进的模糊综合评价法在水质评价中的应用[D].重庆:重庆大学,2014.
(责任编辑:朱彬)
An Evaluation Technique of Water Quality for Guiyang Based on Improved TOPSIS Method
LU Ya-nan,WU You-fu,YANG Zheng-yun
(School of Science, Guizhou Minzu University,Guiyang 550025, China)
Abstract:According to the defect compared with relative progress algorithm when TOPSIS method was used for comprehensive evaluation. In this paper, TOPSIS method was improved , and the combination of AHP and entropy weight method were used for calculating the weight as the weight of each evaluation index in order to avoid the subjectivity and oneness of determining weight. At the same time we set up the water quality evaluation model which combines the combining power, and we improves TOPSIS method and apply it to the evaluation of water quality of Guiyang. The simulation shows that this method is effective.
Key words:evaluation of water quality; technique for order preference by similarity to an ideal solution; entropy weight method
作者简介:吕亚楠,男,安徽淮北人,贵州民族大学理学院硕士研究生。研究方向:应用统计。
基金项目:贵阳市科技项目(2010,2012);贵州省科技厅基金资助项目(2007,2009,2012);贵州省教育厅基金资助项目(2011, 2013[“125计划”])
收稿日期:2015-10-17
中图分类号:X824
文献标识码:A
文章编号:1009-3583(2016)-0091-04
