微差爆破振动波速度峰值-位移分布特征的延时控制*

楼晓明,周文海,简文彬,郑俊杰

(1.福州大学紫金矿业学院，福建 福州 350116；2.福州大学爆炸技术研究所，福建 福州 350116；3.福州大学环境与资源学院，福建 福州 350116；4.华中科技大学土木工程与力学学院，湖北 武汉 430074)

微差爆破振动波速度峰值-位移分布特征的延时控制*

楼晓明1,2,周文海1,简文彬3,郑俊杰4

(1.福州大学紫金矿业学院，福建 福州 350116；2.福州大学爆炸技术研究所，福建 福州 350116；3.福州大学环境与资源学院，福建 福州 350116；4.华中科技大学土木工程与力学学院，湖北 武汉 430074)

为了通过振动波传播规律研究微差爆破延时控制，改善爆破振动和提高爆炸能利用，选取普通雷管和澳瑞凯高精度雷管进行不同段别延期起爆对比实验，试爆过程对振动波测振。基于振动波函数优化理论基础，对实测数据和波状谱处理分析，总结了不同微差时间下振动波传播规律及速度峰值、主频、频带能量、总能量等变化特征，根据该特征发现振动波速度图谱和该速度积分所得位移图谱中两者最大值对应时间点相同。依据此速度峰值-振动位移分布特征，对某实测简单振动波进行高斯多峰拟合，结果表明：该波段能量最大化时间点为60 ms左右，振动最小的时间点为25 ms左右。

爆炸力学；延时控制；多峰拟合；微差爆破；爆破振动；峰值速度

很多学者对微差爆破延时控制振动危害和爆破效果进行了研究，如：D.S.Kim等[1]通过对岩石介质中振动波波谱分析，得出了爆破振动波随微差时间变化的传播规律；娄建武等[2]利用振动信号识别技术，通过观测振动波能量分布特征，给出了最佳爆破控制方案；Y.Lu等[3]通过研究爆破过程中振动波引起的岩石质点模型结构响应规律，探究了最佳延期时间。然而，爆破振动波信号属于随机不稳定元素，利用能量、频谱、小波变换等作为载体给分析带来诸多不便。

本文中，为确保准确性和实用性，进行普通雷管和澳瑞凯雷管不同微差起爆方式的对比测振实验，分析实测振动波信号随微差时间改变过程中振动波传播速度、能量、频率等的变化规律，发现振动波速度峰值对应时间点与该波段积分所得位移波段的最大振动位移对应时间点基本吻合，说明峰值速度可作为降振研究指标[4]。

1 实 验

德尔尼露天矿4 278 m平台紧邻高陡边坡，岩层较破碎。为保证爆破后边坡稳定，将该平台分成并列的普通雷管爆区和澳瑞凯雷管爆区，进行爆破振动对比实验：每爆区划分为3个实验场所，采用相同起爆网络和3种不同微差时间。澳瑞凯雷管爆区3个场所的地表排孔间分别采用(65 ms、17 ms)、(65 ms、25 ms)、(65 ms、42 ms)延期雷管，孔内采用14 m脚线400 ms延期雷管和7 m脚线425 ms延期雷管；普通雷管爆区孔内采用380 ms延期雷管，地表排孔间分别采用(100 ms、25 ms)、(100 ms、50 ms)、(100 ms、75 ms)延期雷管。爆区Ⅰ的网络连线和环境如图1～2所示，图中：左侧孔内采用10段380 ms、排间5段100 ms、孔间2段25 ms普通导爆管雷管；右侧孔内采用17段425 ms、排间5段65 ms、孔间2段17 ms澳瑞凯毫秒延期雷管。

图1 爆破实验起爆网络Fig.1 Initiating circuit of blasting experiment

图2 爆区环境Fig.2 Blasting environments

2 不同延时条件下爆破振动波传播规律

采用Blast-UM型爆破测振仪对两爆区6个实验场所进行测振，每个实验场所有3个测点，每个测点距测振仪空间距离约170 m。

普通雷管爆区Ⅱ测点1，距测振仪水平距离161.92 m，高差64 m，空间距离173.25 m。实测的振动数据见表1，速度波形如图3所示。澳瑞凯雷管爆区Ⅱ测点1，距测振仪水平距离157.43 m，高差64 m，空间距离169.93 m。实测的振动数据见表2，速度波形如图4所示。其中，vm为最大振动速度，tm为最大振动速度对应时间，fh为半波频，fFFT为FFT主频。

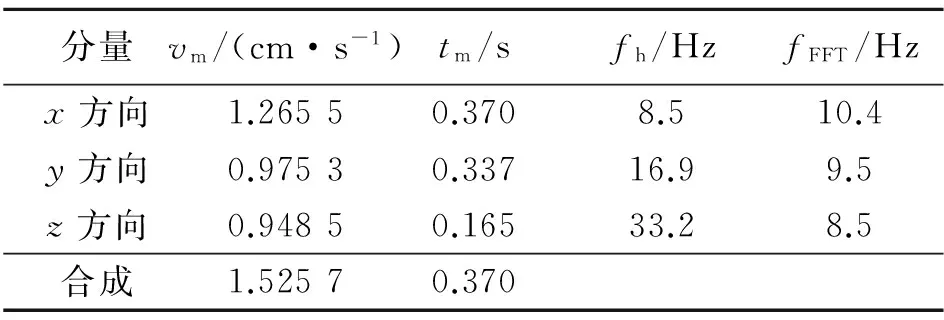
表1 普通雷管爆区Ⅱ测点1数据Table 1 Data of measuring point 1on ordinary detonator blasting area Ⅱ

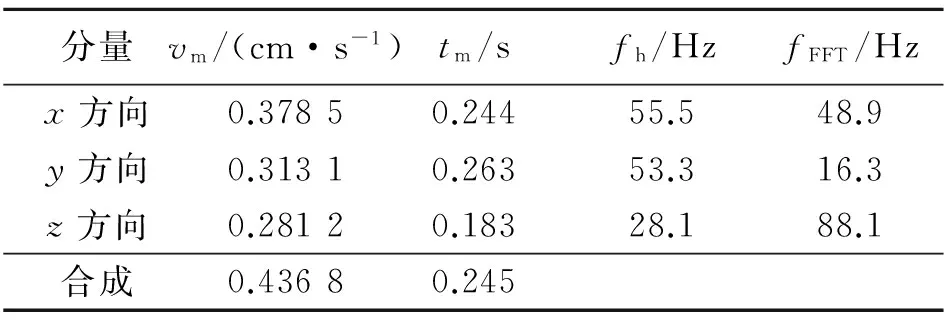
表2 澳瑞凯雷管Ⅱ爆区测点1数据Table 2 Data of measuring point 1on Orica detonator blasting area Ⅱ

实验对比显示：(1)普通雷管爆区振速波形分散、叠加不明显，峰值速度较大；高精度雷管爆区速度波子波较密集，相互叠加干扰现象显著，峰值速度较小。(2)普通雷管爆区振动频率信号远小于澳瑞凯雷管爆区，且多分布在低频带；而澳瑞凯雷管爆区频率信号分布较广，大多集中在中高频频带。证明普通爆区振动波周期较大，波形叠加不够明显。(3)在三轴振动速度信号频谱上，随着微差时间的递增，两爆区的振动波质点合成速度峰值存在收敛性和能量汇聚现象。原因是振动速度函数可表示时域信号，依据振动波叠加原理说明振动波对微差时间存在收敛性[5]。(4)随着振动波的传播，出现子波叠加，波形陡然攀升，澳瑞凯雷管爆区更明显。原因是澳瑞凯雷管精度高，波周期小，拉近了波能叠加密度，使能量汇聚明显，因此澳瑞凯雷管合理延期时间能够更有效地控制爆破效果。

实测的6个实验场所18个测点测振数据见表3。由表3可知：(1)随着雷管微差时间递增，两爆区振动波最大合成速度先减后增，普通爆区变化率更显著，合成速度不稳定性增强，说明微差时间的改变直接影响振动波速度峰值大小。(2)普通雷管爆区振动波出现最高主频对应时间点较分散，数据稳定性较差，而澳瑞凯雷管爆区振动波出现最高主频对应时间点较集中，数据稳定性强；并且两爆区都随微差时间递增，振动波主频率呈递先减后增趋势，且普通雷管爆区变化率更显著。再次证明了澳瑞凯雷管适当的微差时间选取，能够更有效地控制爆破振动效应。最大合成振速和FFT主频，如图5～6所示。

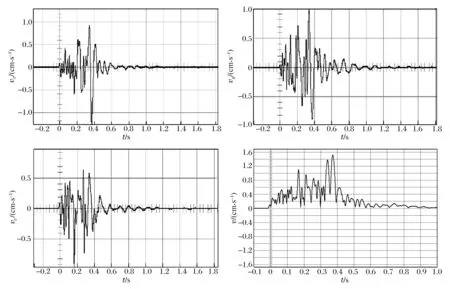
图3 普通雷管爆区Ⅱ测点1速度Fig.3 Velocities of measuring point 1 on ordinary detonator blasting area Ⅱ

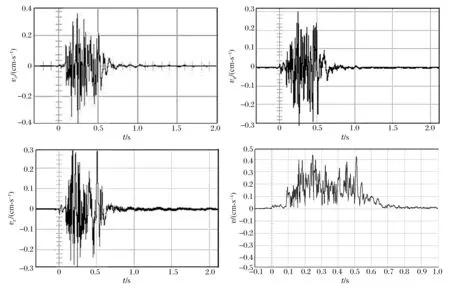
图4 澳瑞凯雷管爆区Ⅱ测点1速度Fig.4 Velocities of measuring point 1 on Orica detonator blasting area Ⅱ

表3 测振数值汇总Table 3 Vibration numerical reservoir

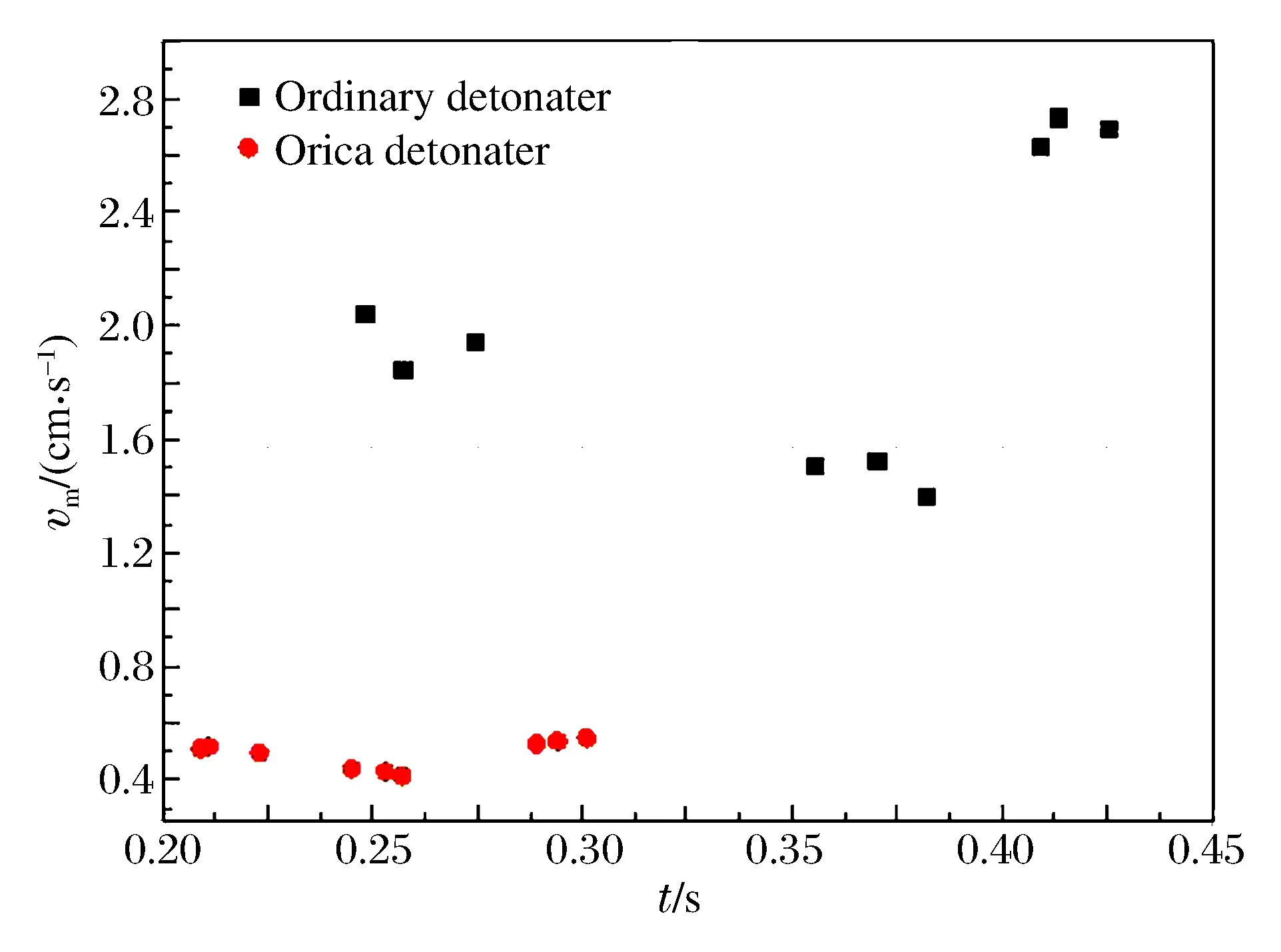
图5 最大合成速度Fig.5 Largest synthesis velocity

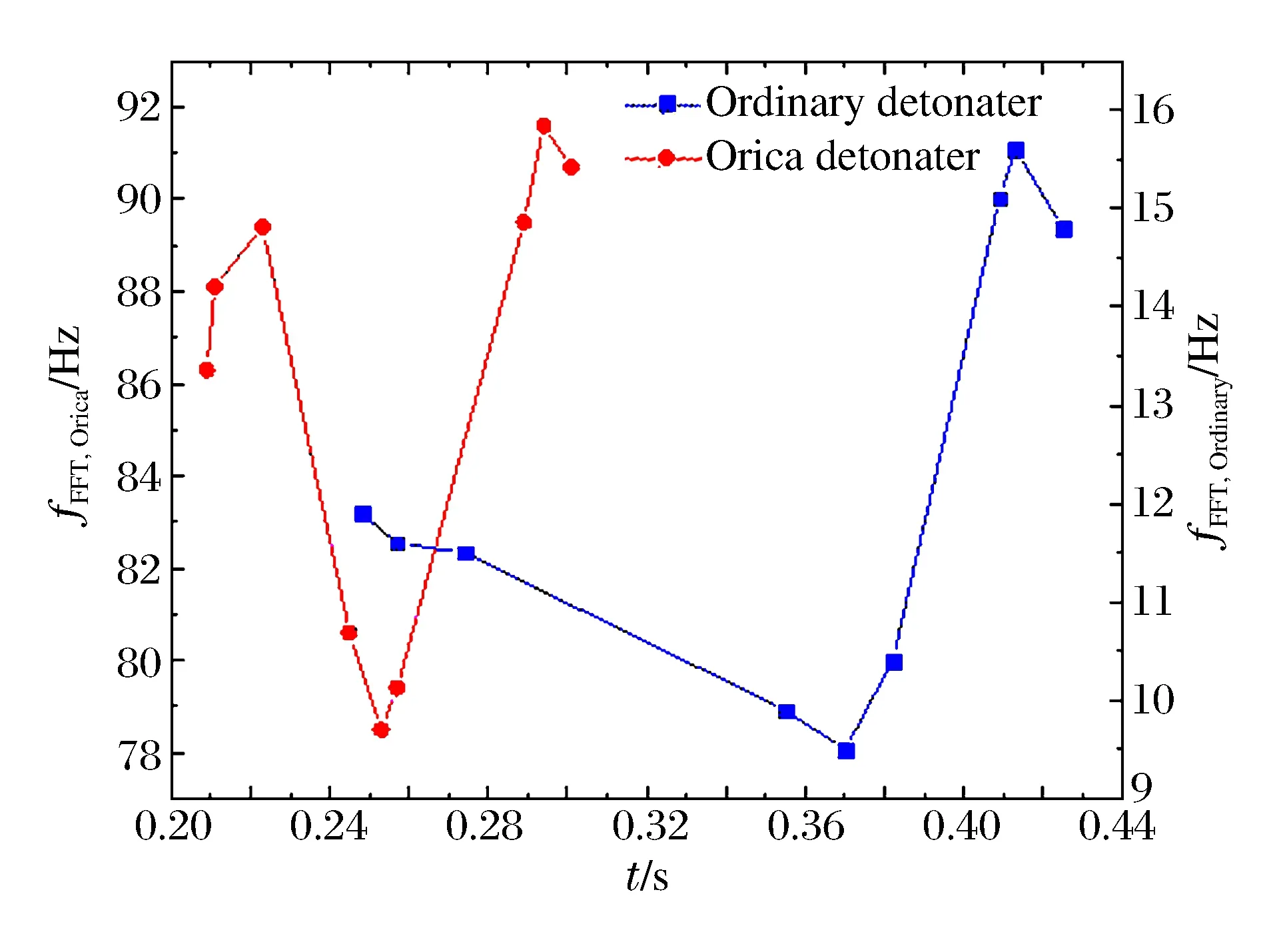
图6 FFT主频Fig.6 FFT main frequency

通过对比实测振动波波段频谱和功率谱，发现：(1)随着微差时间递增，主频持续时间增大，但主频幅值减小。原因是，微差时间不同导致振动信号在传播过程中相位交错叠加，稀疏了叠加密度，致使谷峰衰减。(2)爆破振动波波段能量整体变化趋势为逐渐降低，起初频带能量持续时间无固定规律，但后期高频能量持续时间加长，中间还出现频带能量突变效应，主频持续时间增长与总能量呈线性关系[6]。通过微差时间改变引起振动波段能量变化的规律说明，不同的微差控制既可改善爆破振动的效果，也可以更好地利用爆炸能量。

3 基于谷峰-位移分布特征的延期控制

振动波为多种子波叠加而成，很难用理论时间来控制具体延期起爆。本文中，选取单孔延期起爆测得的振动波(见图7)作为研究对象，将峰值速度-能量分析转化为实测简单波段谷峰-位移分布特征分析。通过对微差爆破获得速度波段分析，确定波段主要的突变点、微差爆破过程中炮孔的微差时间、相邻炮孔间最佳延期时间。

由图7可见，速度波段中出现了6个突出的速度谷峰，分别为：(0.117,0.362)、(0.135,-0.356)、(0.395,0.480)、(0.423,-0.376)、(0.476,-0.492)、(0.495,0.383)。图8为该振动波速度波段积分所得的振动位移。当t=0.476 s时，振动波速度达到峰值0.492 cm/s，此刻，振动位移s=0.003 2 cm也达到最大，所以可确定该时间点为该振动波叠加能量最大(振动最严重)。

爆破能量最大化的时间点和爆破振动最小时间点的确定，对爆破振动至关重要。为获得简单、叠加干扰较少的波形，在爆区附近实施单孔延期试爆，用测振仪获取该波段三轴速度与对应时间，导入Excel进行矢量合成，得到合成速度。将该数据导入Origin 9.0软件，绘制的合成速度如图9所示。

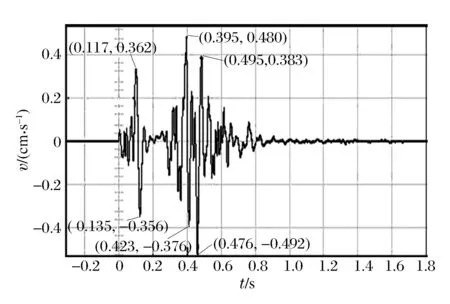
图7 振动波峰值Fig.7 Vibrated peak positions

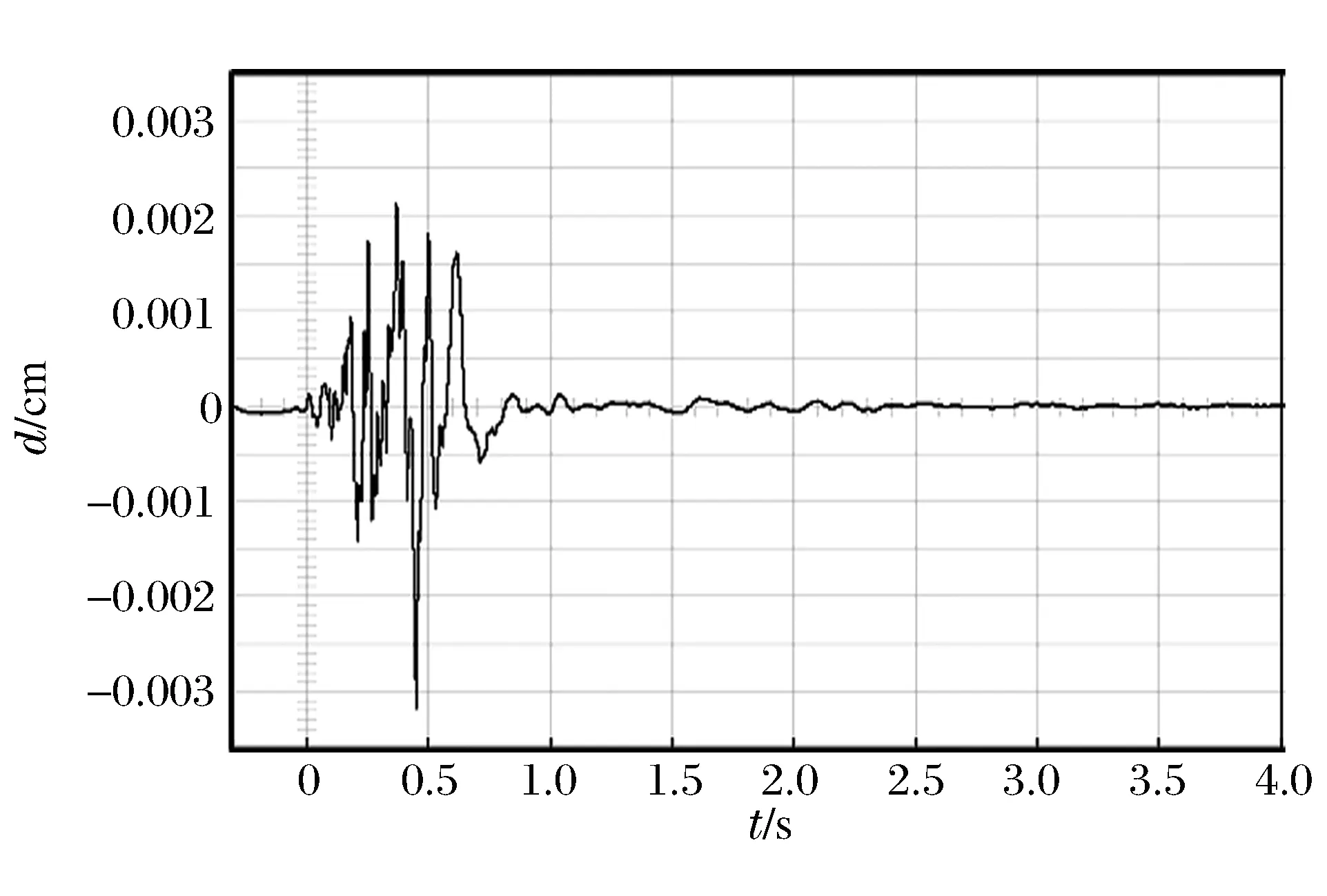
图8 地面振动位移Fig.8 Vibrated displacements

图9 合成速度Fig.9 Synthetic velocity

通过上述研究和速度波段积分原理可知，速度波段中主要的突变点(波峰、波谷)可作为延期控制降振研究对象。为获取该波段谷峰主要信息，对该波段采取多峰拟合，整个过程用高斯法进行数据拟合。采用最小方差原则，对高斯参数调整和限定，可得到各峰值高度、宽度、峰区面积、峰中心位置及对应时间等。为获取能量最大化和爆破振动最小时间点，对该波段谷峰分别进行拟合，由于诸多隐峰的存在，所以拟合关键步骤为寻峰。

图10～11为最小峰值的分布点和拟合曲线，表4～5为最小峰值的区间参数和速度方差。最小峰值(波谷)拟合显示：相关系数Adj.R-square=0.975 56(接近1)，表明数据相关性较好，能够有效地反映振动波质点的离散程度；卡方系数Reduced Chi-Sqr=0.136 32(趋近0)，也表明拟合值与实际值之间偏差程度尚可接受。所以，可用此最小峰值拟合作为研究样本。通过图11最小峰值(波谷)拟合曲线观察发现，多峰拟合积累曲线突出集中处对应时间点为25 ms左右，根据上述合成速度积分理论可知，该处振动位移最小，可作为爆破振动最小时间点。吴贤振等[7]通过LS-DYNA动力有限元软件模拟多段微差爆破效果，结果显示最佳降振时间为25 ms左右，与本文实验结果一致。

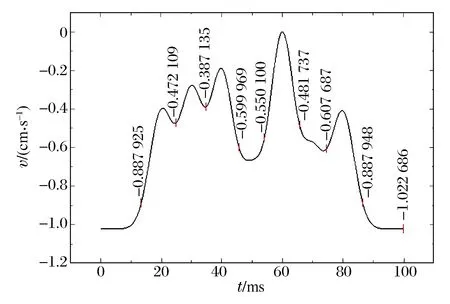
图10 最小峰值分布点Fig.10 Minimum peak distribution points

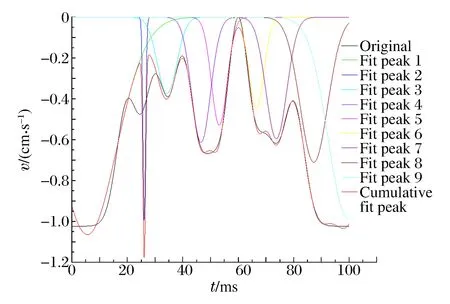
图11 最小峰值拟合曲线Fig.11 Minimum peak fitting curves

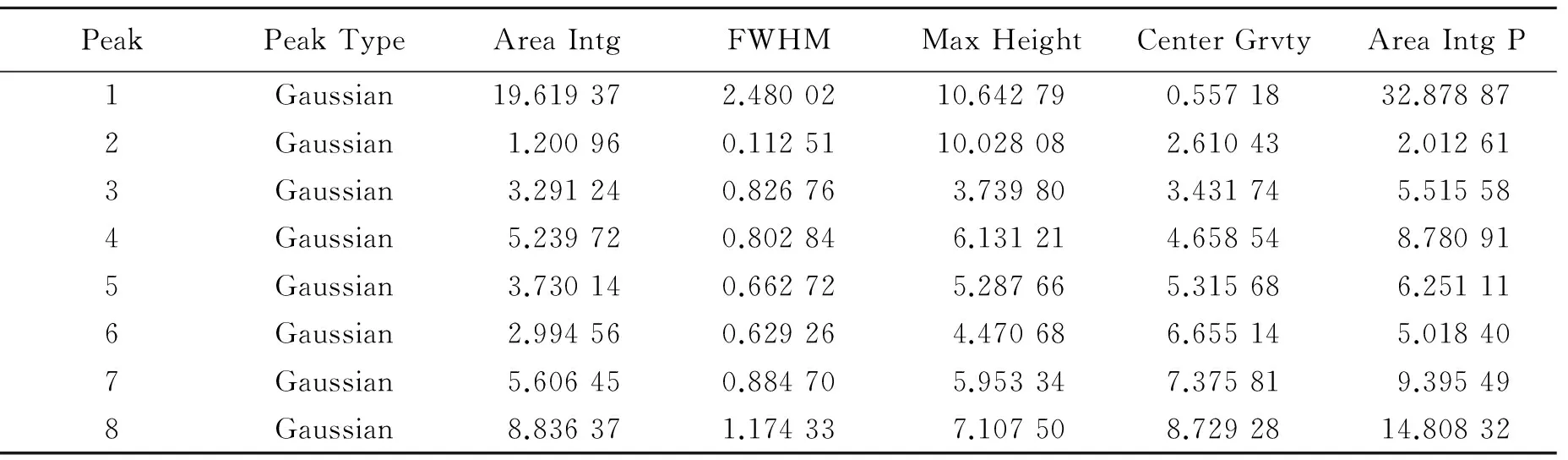
表4 最小峰值区间参数Table 4 Minimum peak interval parameters

表5 最小峰值时间-速度方差Table 5 Minimum peak time and velocity variance

图12～13为最大峰值的分布点和拟合曲线，表6～7为最大峰值的区间参数和速度方差。同样，最大峰值(波峰)拟合显示：相关系数Adj.R-square=1，卡方系数Reduced Chi-Sqr=1.940 75×10-8，表明该拟合值与实际值基本吻合，可作为研究样本。通过图13最大峰值拟合曲线观察发现，多峰拟合积累曲线集中处对应时间点为60 ms左右，所以该时间点对应的振动位移最大，可作为爆破能量利用最大化时间点。

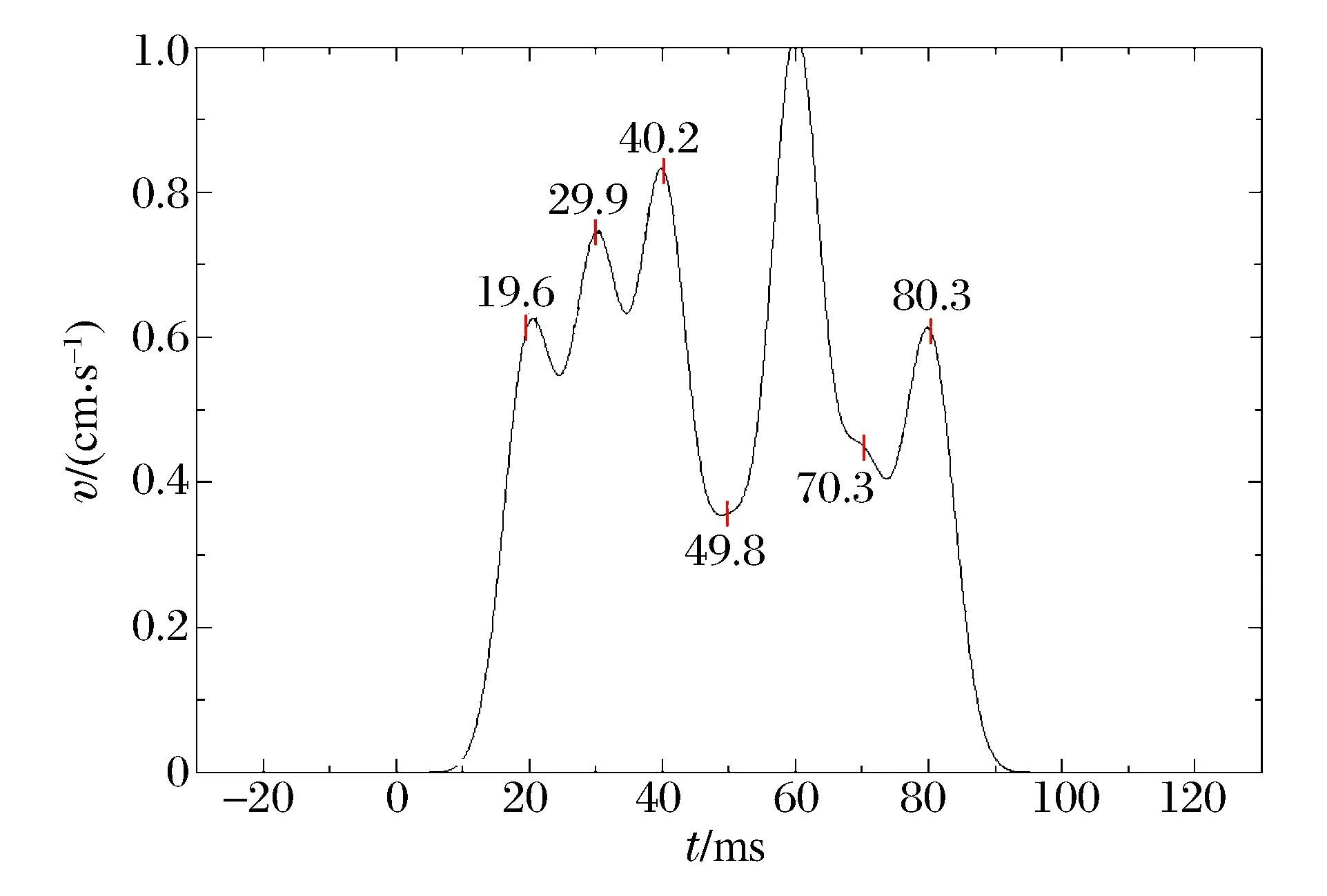
图12 最大峰值分布点Fig.12 Maximum peak distribution points

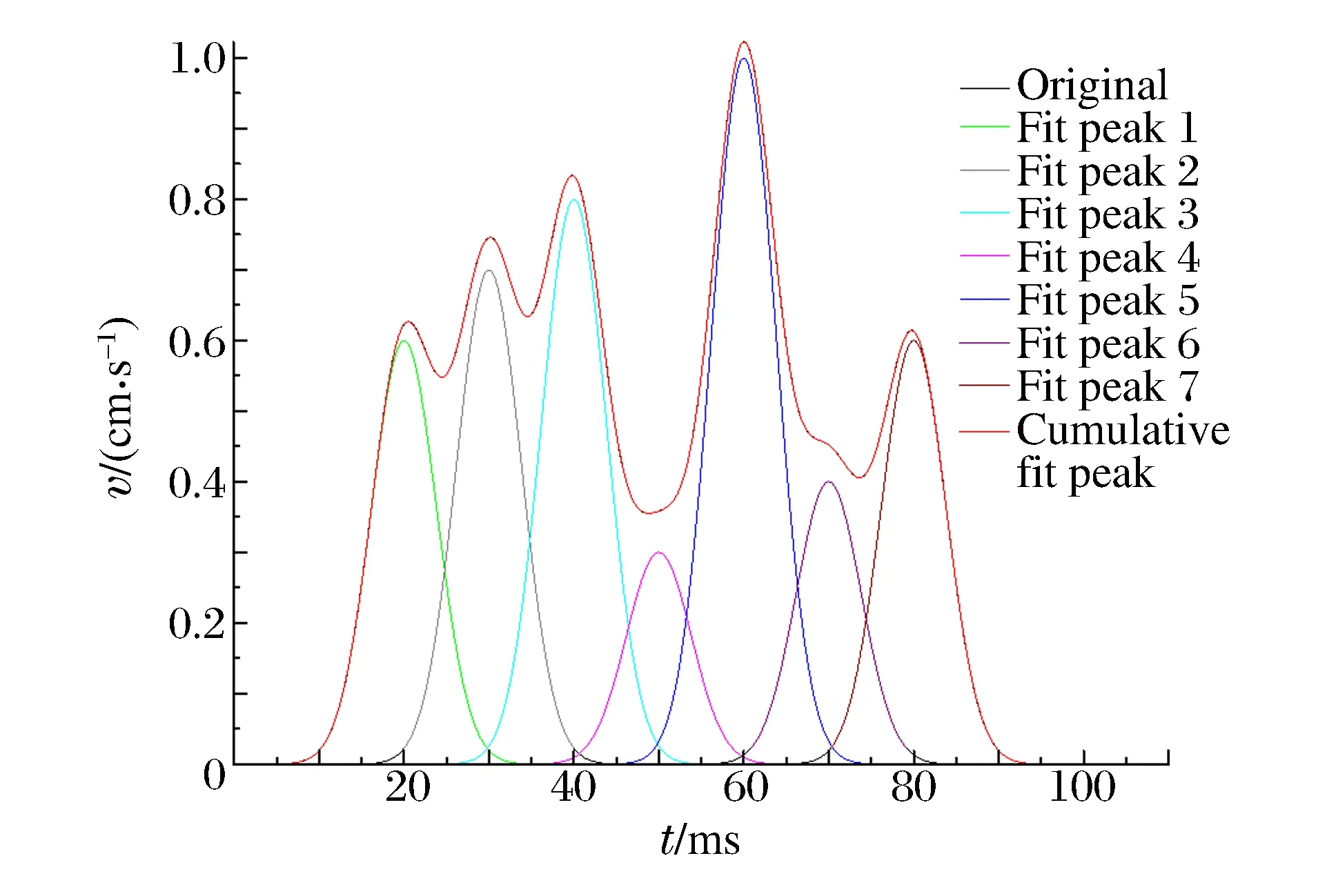
图13 最大峰值拟合曲线Fig.13 Maximum peak fitting curves

表6 最大峰值区间参数Table 6 Maximum peak interval parameters

表7 最大峰值时间-速度方差Table 7 Maximum peak time and velocity variance

4 结 论

(1)普通雷管起爆产生的振动波波形较分散，波形叠加较少，峰值速度较大，振动主频分布在低频带；澳瑞凯雷管起爆产生的振动波波形叠加干扰严重，速度峰值较小，振动频率信号分布较广，多集中在中高频带，在三轴振动速度频谱上，能量和速度汇聚现象显著。说明在工程爆破中高精度雷管比普通雷管爆破效果好。

(2)随着微差时间的递增，爆破振动波波段能量整体变化极不稳定，主频持续时间增长与总能量呈线性关系，质点合成峰值速度与主频存在收敛性，合成速度和主频都出现先衰减后增强的趋势。其中普通雷管爆区变化率远高于澳瑞凯雷管爆区，数据不稳定性更大。

(3)根据振动波速度图谱和该速度积分所得位移图谱，发现两者最大值(速度峰值和最大振动位移)对应时间点吻合，依据此速度峰值-振动位移分布规律对实测简单速度波形进行多峰拟合，利用拟合所得积累曲线可得到该波段能量最大化和爆破振动最小状态对应时间点。

[1] Kim D S, Lee J S. Propagation and attenuation characteristics of various ground vibrations[J]. Soil Dynamics and Earthquake Engineering, 2000，19(1)：115-126.

[2] 娄建武，龙源.爆破震动信号的特征提出及识别技术研究[J].振动与冲击，2003，22 (3)：80-82. Lou Jianwu, Long Yuan. Study on the technique of take and identify characteristics of blasting seismic wave[J]. Journal of Vibration and Shock Wave, 2003，22 (3)：80-82.

[3] Lu Y, Hao H, Ma G, et al. Simulation of structural response under high-frequency ground excitations[J]. Earthquake Engineering & Structural Dynamics, 2001，30(2)：307-325.

[4] 李洪涛，杨兴国，卢文波,等.基于等效峰值能量的建筑物爆破振动安全评价探讨[J].岩土工程学报，2011，33(5)：821-825. Li Hongtao, Yang Xingguo, Lu Wenbo, et al. Safety assessment for structures under blasting vibration based onequivalent peak energy[J]. Chinese Journal of Geotechnical Engineering, 2011，33(5)：821-825.

[5] 郭学彬，张继春，刘泉,等.微差爆破的波形叠加作用分析[J].爆破，2006，23(6)：4-8. Guo Xuebin, Zhang Jichun, Liu Quan, et al. Analysis of wave from superimposed action of millisecond blasting[J]. Blasting, 2006，23(6)：4-8.

[6] 林大超，施惠基，白春华,等.爆炸地震效应的时频分析[J].爆炸与冲击，2003，23(1)：31-36. Lin Dachao, Shi Huiji, Bai Chunhua, et al. Time-frequency analysis of explosion seismic effects[J]. Explosion and Shock Waves, 2003，23(1)：31-36.

[7] 吴贤振，尹丽冰，刘建伟.基于LS-DYNA的临近采空区多段爆破微差时间优化研究[J].爆破，2015，32(1):87-92. Wu Xianzhen, Yin Libing, Liu Jianwei. Optimization of blasting delay time near underground goaf based on LS-DYNA[J]. Blasting, 2015，32(1)87-92.

(责任编辑 丁 峰)

Control of delay time characterized by distribution of peak velocity-displacement vibration of millisecond blasting

Lou Xiaoming1,2, Zhou Wenhai1, Jian Wenbing3, Zheng Junjie4

(1.CollegeofZijinMining,FuzhouUniversity,Fuzhou350116,Fujian,China;2.InstituteforExplosiveTechnology,FuzhouUniversity,Fuzhou350116,Fujian,China;3.CollegeofEnvironmentandResources,FuzhouUniversity,Fuzhou350116,Fujian,China;4.CollegeofCivilEngineeringandMechanics,HuazhongUniversityofScienceandTechnology,Wuhan430074,Hubei,China)

In order to improve the blasting vibration and boost the efficiency of blasting energy, this paper mainly focuses on the delay time control research through transmission law. We performed an experiment with a delayed-detonation scheme in different period, which selects common detonator and Orica high precision detonator. The measured vibration of the earthquake wave is based on seismic wave function optimization theory foundation. The measured data and wavy figure were acquired through it, then we found out the variation characteristics of the rules of earthquake wave propagation, peak velocity, domain frequency, band energy and the total energy in different delayed period. At the same time, according to the characteristics to find velocity map which Synthesized by triaxialvibration wave and displacement map which assembled by speed Calculus correspond to the maximum in same time. On the basis of peak velocity-vibration displacement distribution characteristics, fitting method for Gaussian multi-peak is applied for measured vibration wave, to give the band energy maximize time points aboutt=60 ms, blasting vibration around the minimum time fort=25 ms.

mechanics of explosion; time delay control; multi-peaks fitting; millisecond blasting; blasting vibration; peak velocity

10.11883/1001-1455(2016)06-0839-08

2015-04-09； < class="emphasis_bold">修回日期：2015-07-01

2015-07-01

国家自然科学基金项目(41072232)；福建省自然科学基金项目(2011J01310)

楼晓明(1972— )，男，博士，副教授，Lxm@fuz.edu.cn。

O382.2 <国标学科代码：1303520 class="emphasis_bold"> 国标学科代码：1303520 文献标志码：A国标学科代码：1303520

A