循环爆破开挖下隧道围岩振动效应与损伤演化的模型实验*

中国生,敖丽萍,付玉华

(1.惠州学院建筑与土木工程学院，广东 惠州 516007；2.江西理工大学应用科学学院，江西 赣州 341000)

循环爆破开挖下隧道围岩振动效应与损伤演化的模型实验*

中国生1,敖丽萍1,付玉华2

(1.惠州学院建筑与土木工程学院，广东 惠州 516007；2.江西理工大学应用科学学院，江西 赣州 341000)

针对推进式循环爆破开挖下隧道围岩振动效应与损伤演化问题，按照相似比理论进行模型实验研究，实验模型采用1∶15比例浇筑制成。通过模拟隧道推进式循环爆破开挖方式，以同一测点处爆破前后岩体声速变化评价隧道围岩损伤程度，探寻爆破参量变化对振动效应的影响，探索围岩损伤演化与爆破次数之间的关系。研究结果表明：在最大段药量大致相同情况下，起爆段数对萨道夫斯基公式的介质系数K影响很小，而对萨道夫斯基公式的衰减系数α影响较大；隧道在推进式循环爆破开挖下，同一深度距离爆区相同的测点，其声速降低率存在较大差异，围岩的爆破损伤范围在深度和广度方面均具有典型的各向异性特征；当爆炸参量基本相同时，不同循环爆破开挖下测点的累积声速降低率呈非线性增长趋势；在推进式循环爆破加载下，围岩爆破累积损伤量D与爆破次数n之间存在非线性演化特性，不同的测点具有各自的爆破累积损伤扩展模型，距离爆源越近爆破损伤扩展越快，围岩爆破累积损伤效应具有典型的非线性演化特性和各向异性特征。

爆炸力学；振动效应；模型实验；隧道开挖；循环爆破加载；围岩损伤

钻孔爆破是矿山开采、隧道(巷道)开挖、地下硐室建设等工程岩体开挖中常用和高效的施工手段。爆破施工完成工程岩体开挖的同时，不可避免地对周围岩体产生不利影响。循环爆破掘进对围岩的振动效应，导致围岩内壁应力快速释放，不可避免地对围岩产生损伤，并使其表层岩体力学参数大幅下降，形成所谓的爆破松动区，严重时可能引起保留岩体的局部开裂甚至失稳。同时，爆破松动区的形成还可能加剧岩体的后续卸荷松弛效应，给工程的安全施工和正常运行留下了隐患。

为此，对爆破作业产生的围岩损伤问题，有了卓有成效的研究。D.E.Grady等[1]提出，在爆破荷载作用下，原岩中的裂纹扩展且服从指数分布规律，引入损伤变量D表示裂纹开裂引起的岩石强度降低。L.M.Taylor等[2]提出了损伤变量D、裂纹密度和有效体积模量及有效泊松比之间的关系，扩大了损伤模型的适用性。T.J.Ahrens 等[3]将材料的裂纹发育和纵波波速变化联系起来，以纵波波速变化评价岩石材料微裂纹的发育程度，这是一种简单而有效的方法。I.L.Meglis等[4]基于超声波速度和振幅对裂纹的敏感性，应用超声层析成像法，研究了加拿大原子能地下实验室隧道开挖诱发的围岩损伤问题。马建军[5]在现场监测了回采爆破过程中围岩声波速度变化情况，分析了岩体损伤演化规律。Yan Changbin[6]基于声波测试原理，对厂坝铅锌矿某巷道围岩在爆破作用下产生的累积损伤效应进行了现场实验研究。夏祥等[7]通过多次爆破前后声波波速的变化率，开展了三峡临时船闸和核电基础开挖岩体的损伤特性研究。张国华等[8]结合大帽山大断面隧道群的现场声波监测，研究了推进式往复爆破作业的双侧壁导坑法施工的大断面隧道的围岩累积损伤范围。杨国梁等[9]利用超声波测试技术，对巷道侧壁爆破损伤进行了研究，揭示了爆破振动下岩体的损伤累积规律。目前，声波检测方法仍然是研究岩体爆破损伤问题最常用、高效的测试技术[10-15]。

然而，上述相关研究大多在单孔装药的一次爆破或在单孔装药多次重复爆破等较理想的情况下进行的，与岩体工程实际的爆破作业方式并不相符，而实际的矿山开采、隧道(巷道)开挖、地下硐室建设等岩体工程开挖均采用推进式、往复式的循环多段延时爆破作业。因此，针对推进式循环爆破作业导致的围岩振动效应与损伤演化特性，很有必要进行深入而系统的研究。为此，本文中，以某铜矿运输巷道某施工标段爆破开挖为模拟对象，设计并制作相似材料模型，用于模拟运输巷道钻爆法施工开挖过程，分析推进式循环爆破开挖对隧道围岩振动效应及损伤作用机理。

1 相似材料模型实验

1.1 模型缩尺比例和相似材料模型

根据该铜矿运输巷道开挖断面的实际尺寸，以及室内实验场地的空间大小，最终确定实验模型缩尺比例为1∶15。这符合相似理论规定的实验模型缩尺比例的合理范围(1∶20～1∶4)[16]。因此，根据实验模型的缩尺比例确定模型尺寸为3 000 mm×3 000 mm×2 500 mm。

图1 相似材料配比试件强度实验Fig.1 Strength experiment of samples with similar material ratios

武山铜矿运输巷道施工标段围岩主要为灰岩岩层，以灰岩岩体为围岩模拟对象。通过现场岩芯取样，经岩石力学实验获得灰岩岩石平均单轴抗压强度σc=103.6 MPa、平均弹性模量E=48.5 GPa，通过对现场开挖段和掌子面的地质调查，参照Hoek-Brown经验强度准则，估算灰岩围岩岩体抗压强度σm=30.5 MPa、变形模量Em=27.8 GPa。模型相似材料选天然石英砂、粒径2～4 cm的碎石或卵石为骨料，参照JGJ 55-2011《普通混凝土配合比设计规程》，用强度32.5 MPa的硅酸盐水泥，配出强度为31.1 MPa、弹性模量为29.3 GPa的相似材料用来模拟灰岩围岩。图1为实验室进行相似材料配比试件的强度实验。

1.2 爆破作业

根据相似理论[16]，相似材料模型爆破实验应与隧道开挖推进式循环爆破作业方式一致。模型实验每个循环爆破作业均采用掏槽眼、崩落眼和周边眼等3次爆破形式，1次循环爆破开挖进尺约300 mm，进行4个循环的爆破开挖，共计12次爆破作业，本次实验隧道推进式循环爆破开挖总长约1 200 mm。

由本次实验模型的缩尺比例确定的模拟隧道开挖截面尺寸，隧道爆破开挖断面的炮孔布置如下：最里圈为掏槽眼、中间圈为崩落眼、最外圈为周边眼，采用先掏槽、再崩落、后周边的分次爆破顺序，以及延时起爆方式，如图2所示。经过4个循环爆破开挖，共计12次爆破作业后，模型实验隧道爆破开挖的实物照片，如图3所示。

图2 隧道截面尺寸与炮孔布置图Fig.2 Tunnel section size and blasting hole layout

图3 模型实验的隧道爆破开挖Fig.3 Tunnel blasting excavation for model experiment

采用乳化炸药，为了提高和改善爆破效果，装药方式为耦合装药，装药时将炸药捣入孔底，捣压密实并使之紧贴孔壁，采用黏土制作炮泥堵塞炮孔，堵塞长度约150～200 mm。模型实验的掏槽眼、崩落眼和周边眼爆破均采用延时爆破起爆，根据相似理论和隧道开挖截面尺寸，可确定循环爆破作业所需的毫秒延时雷管段位数，具体爆破参数见表1。

表1 模型隧道循环爆破作业的爆破参数Table 1 Blasting parameters for circulation blasting in tunnel model

图4 模型实验的测点布置图Fig.4 Layout of measuring points of model experiment

1.3 实验测试

围岩损伤检测采用武汉中岩科技有限公司的RSM-SY5型智能声波检测仪，它具有操作简单、携带方便、性能可靠以及功能强大等特点。为了全面检测隧道推进式循环爆破开挖导致的围岩损伤程度，由隧道推进式循环爆破开挖的总长1 200 mm，在隧道围岩的上方、左侧分别布置了3个平行等距的检测剖面，平行隧道开挖走向钻取了11个孔径为50 mm、孔深为1 200 mm的测试孔，如图4所示。

采用一发一收跨孔测试方式，检测时在测试孔注满盐水作为耦合剂，且发射和接收探头始终保持在同一个水平面，爆破前后均需对6个检测剖面进行声波测试。因隧道循环爆破开挖的总长为1 200 mm，除去换能器探头端部，实际每个剖面的测试深度均为1 150 mm，测试步距为50 mm，一个剖面共需测试23次，模型实验声波测试的实物照片，如图5所示。

爆破振动测试采用Blastmate Ⅲ爆破振动监测仪，它具有检测频带宽、量程大和精度高等特点，速度传感器为三向地震检波器。测试时，拾振器布置在每个声波检测剖面的中央，共计布置了6台，如图4所示。为了提高爆破振动监测的效果，特地使用膨胀螺栓将速度传感器牢牢地固定在模型上，实验现场爆破振动测试的实物照片，如图6所示。

图5 模型实验的声波测试Fig.5 Acoustic measurement of model experiment

图6 模型实验的振动测试Fig.6 Vibration measurement of model experiment

2 结果与分析

2.1 围岩振动效应

由文献[17]，炸药爆炸引起介质内部的质点振动有垂直、径向和切向3个速度分量，在高差不大和近距离范围的情况下，一般是垂直速度分量对爆破振动起控制作用。因此，本文中选择垂直质点振动速度作为监测量。

模型实验隧道爆破开挖采用了掏槽眼、崩落眼和周边眼等3种爆破作业，每次作业均进行了爆破振动监测，3种爆破作业产生的典型爆破振动速度，如图7所示。

从图7可以看出，掏槽眼、崩落眼和周边眼等爆破监测的振动速度曲线，分别存在4、7和11个峰值。可见，延时分段爆破效果十分明显，并与表1中所列的起爆雷管段位分布情况完全对应。

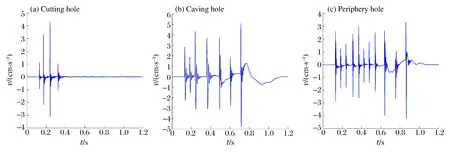
图7 爆破振动曲线Fig.7 Blasting vibration curves

隧道推进式循环爆破开挖的掏槽眼、崩落眼和周边眼等3种爆破作业监测的相关数据，见表2。由表2可知：在相同的地质环境下，当爆心距相同时，起爆段数越多，爆破地震波的主频越高；在同一炮次爆破下，爆心距越大，爆破地震波的主频越低；峰值质点振动速度PPV取决于最大段药量和爆心距，符合萨道夫斯基公式。萨道夫斯基公式为：

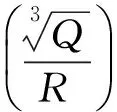
(1)

式中：v为峰值质点振动速度(cm/s)，K为介质系数，Q为最大段药量(kg)，R为爆心距(m)，α为衰减系数。

表2 爆破振动监测的相关数据Table 2 Related data of blasting vibration monitoring

由文献[12]，由于隧道循环爆破开挖采用分段起爆方式，因此起爆点与测点之间的距离需采用等效距离代替。等效距离和最大段等效药量为：

(2)

式中：R′为等效距离(m)，Q′为最大段等效药量(kg)，qi为第i个炮眼的药量(kg)，ri为第i个炮眼离测点的距离(m)。

根据爆破振动的监测数据，先由式(2)分别计算各个测点在每次爆破时的等效距离和最大段等效药量，再以式(1)采用最小二乘法，对监测数据按起爆段数不同分别进行线性回归分析，确定介质系数K、衰减系数α和线性回归分析的相关系数γ，见表3。以4个起爆段数的爆破监测数据为例，其线性回归分析如图8所示。

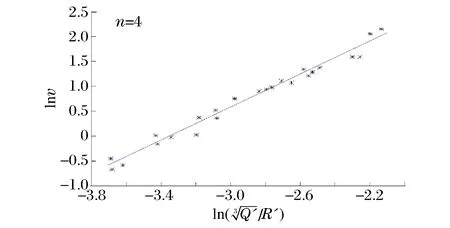
图8 监测数据的线性回归分析图Fig.8 Linear regression analysis of monitoring data

表3 爆破振动监测数据线性回归分析的参数Table 3 Parameters of linear regression analysisof blasting vibration monitoring data

由表3可知，起爆段数对萨道夫斯基公式的介质系数K影响很小，而对萨道夫斯基公式的衰减系数α影响较大。其主要原因是：在相同的地质环境下，起爆段数越多，产生的爆破地震波的主频较高，而高频信号在岩土传播中衰减较快；另外，针对起爆段数相同的爆破监测数据，进行爆破振动效应分析，其相关性更好。由此可见，起爆段数对爆破振动效应的影响不容忽视。

2.2 围岩累积损伤演化特性

由文献[12-15]，可采用岩体声速在爆破前、后的变化率η来判定爆破荷载作用下岩体的破坏程度：

(3)

式中：c′为岩体爆破后的声速，c为岩体爆破前的声速。

由弹性波理论，可将岩体损伤变量D表示为：

(4)

根据DL/T 5389-2007《水工建筑物岩石基础开挖工程施工技术规范》，当爆破前、后岩体声速降低率η>10%时，即判定岩体发生损伤破坏。因此，取ηcr=10%代入式(4)，可计算获得对应的损伤变量阈值Dcr=0.19。

图9 循环爆破开挖前各测试剖面的声速分布Fig.9 Acoustic velocity of each experiment section before cyclic blasting excavation

循环爆破开挖前各测试剖面的声波速度，如图9所示。各测试剖面的声速离散地分布在4.37～4.64 km/s之间，且没有随着测试孔深度增加而递增，这充分说明了实验模型浇筑较均匀密实。各剖面声波速度的差异值(即离散性)反映了实验模型结构强度的各向异性特征。

经过4个循环爆破开挖(共12次爆破)后，各测试剖面声速降低率，如图10所示。同一测试剖面不同深度的测点，随着循环爆破开挖向下推进，其声速降低率基本呈递减趋势；不同测试剖面同一深度的测点，距离爆区越近，其声速降低率越大。在推进式循环爆破加载下，以岩体声速降低率10%作为围岩爆破损伤阈值，以距离爆区相同的3组剖面(即AB与AC剖面、DE与FG剖面、HI与JK剖面)加以分析可知：AB剖面损伤深度为0.85 m，AC剖面为0.75 m，DE剖面为0.15 m、而FG、HI与JK剖面则没有损伤。由此可见，隧道循环爆破开挖下，围岩的爆破损伤范围在深度和广度方面，均具有典型的各向异性特征。

AB测试剖面0.15 m测点的声速降低率与爆破次数的相关性，如图11所示。在爆炸参量(即最大段药量、起爆段位和炸药埋深)大致相同情况下，同一循环的3次爆破(即掏槽眼爆破、崩落眼爆破和周边眼爆破)对同一测点的声速降低率的影响大致相同，累积声速降低率基本上呈线性增长趋势。第1循环爆破开挖时0.15 m测点的声速降低率最大，随着循环爆破开挖向下延伸，围岩声速降低率越来越小，第4循环开挖爆破对0.15 m测点的声速降低率几乎没有影响。因此，在爆炸参量基本相同的情况下，不同循环爆破开挖对同一剖面测点的累积声速降低率呈非线性增长趋势。

图10 4个循环爆破开挖后各测试剖面的声速降低率Fig.10 Decrease rate of acoustic velocity of each experiment section after four cyclic blasting excavations

图11 AB剖面0.15 m测点声速降低率与爆破次数的相关性Fig.11 Correlation of decrease rate of acoustic velocity of 0.15 m measuring point on section AB and times of blasting

对AB、DE剖面0.15 m测点爆破累积损伤量进行非线性拟合分析，如图12所示。可建立相应测点的爆破累积损伤扩展模型：

图12 循环爆破开挖下不同测点的累积损伤扩展曲线Fig.12 Growth curves of the cumulative damage for different measuring points under cyclic blasting excavation

D1=0.291 03-0.302 45e-n/5.136 6,

(5)

(6)

式中：n为爆破次数，D1、D2为测点爆破累积损伤量的拟合值，R1、R2为非线性拟合的相关系数。

由图12和式(5)～(6)可知，根据实验结果建立的爆破累积损伤扩展模型，非线性拟合的相关系数接近于1，能充分反映爆破累积损伤量D与爆破次数n之间的非线性演化特性。在相同的循环爆破作用下，不同的测点具有各自的爆破累积损伤演化规律，距离爆源越近爆破损伤扩展越快。因此，循环爆破开挖下的围岩累积损伤具有典型的非线性增长趋势和各向异性特征。

3 结 论

(1) 在隧道开挖的循环爆破作业中，爆破参数设计除了控制最大段药量外，还需注意起爆段数对爆破振动效应的影响。在最大段药量大致相同情况下，起爆段数对萨道夫斯基公式的介质系数K影响很小，而对萨道夫斯基公式的衰减系数α影响较大。采用合理的起爆段位，既可取得较好的岩体破碎效果，又有利于控制围岩的稳定性。

(2) 在推进式循环爆破开挖下，隧道同一测试剖面不同深度的测点，随着循环爆破开挖向下推进，其声速降低率基本呈递减趋势；不同测试剖面同一深度的测点，距离爆区越近，其声速降低率越大。同一深度距离爆区相同的测点，其声速降低率存在较大差异，围岩的爆破损伤范围在深度和广度方面均具有典型的各向异性特征。

(3) 在相同的循环开挖爆破作用下，围岩声速降低率、爆破累积损伤量与爆破次数之间并非简单叠加，而是一种非线性变化关系；在爆炸参量基本相同的情况下，不同循环爆破开挖对同一剖面测点的累积声速降低率呈非线性增长趋势；测试剖面各个测点的爆破累积损伤扩展模型是不同的，具有各自的爆破累积损伤演化规律，围岩累积损伤效应具有典型的非线性演化特性和各向异性特征。

应当指出的是，上述结论仅在模型实验中获得，仍需实际岩体工程的循环爆破开挖作业验证。

[1] Grady D E, Kipp M E. Continuum modeling of explosive fracture in oil shale[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1980，17(3)：147-157.

[2] Taylor L M, Chen E P, Kuszmaul J S. Micro-crack induced damage accumulation in brittle rock under dynamic loading[J]. Computer Methods in Applied Mechanics and Engineering, 1986，55(3)：301-320.

[3] Ahrens T J, Rubin A M. Impact-induced tensional failure in rock[J]. Journal of Geophysical Research, 1993，98(E1)：1185-1203.

[4] Meglis I L, Chow T M, Martin C D. Assessing in situ microcrack damage using ultrasonic velocity tomography[J]. International Journal of Rock Mechanics and Mining Sciences, 2005，42(1)：25-34.

[5] 马建军.岩石爆破的相对损伤与损伤累积计算[J].岩土力学，2006，27(6)：961-964. Ma Jianjun. Relative damage and computation of damage cumulation for blasting in rock[J]. Rock and Soil Mechanics, 2006，27(6)：961-964.

[6] Yan Changbin. Blasting cumulative damage effects of underground engineering rock mass based on sonic wave measurement[J]. Journal Central South University of Technology, 2007，14(2)：230-235.

[7] 夏祥，李俊如，李海波，等.广东岭澳核电站爆破开挖岩体损伤特征研究[J].岩石力学与工程学报，2007，26(12)：2510-2517. Xia Xiang, Li Junru, Li Haibo, et al. Study on damage characteristics of rock mass under blasting load in Ling’ao nuclear power station, guangdong province[J]. Chinese Journal of Rock Mechanics and Engineering, 2007，26(12)：2510-2517.

[8] 张国华，陈礼彪，夏祥，等.大断面隧道爆破开挖围岩损伤范围试验研究及数值计算[J].岩石力学与工程学报，2009，28(8)：1610-1619. Zhang Guohua, Chen Libiao, Xia Xiang, et al. Numerical simulation and experimental study of damage range of surrounding rock in large tunnel under blasting excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2009，28(8)：1610-1619.

[9] 杨国梁，杨仁树，车玉龙.周期性爆破振动下围岩的损伤累积效应[J].煤炭学报，2013，38(增刊1)：25-29. Yang Guoliang, Yang Shuren, Che Yulong. Damage accumulative effect of surrounding rock under periodic blasting vibration[J]. Journal of China Coal Society, 2013，38(Suppl 1)：25-29.

[10] 严鹏，卢文波，陈明，等.深部岩体开挖方式对损伤区影响的试验研究[J].岩石力学与工程学报，2011，30(6)：1097-1106. Yan Peng, Lu Wenyuan, Chen Ming, et al. In-situ test research on influence of excavation method on induced damage zone in deep tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2011，30(6)：1097-1106.

[11] 胡英国，卢文波，金旭浩，等.岩石高边坡开挖爆破动力损失的数值仿真[J].岩石力学与工程学报，2012，31(11)：2204-2213. Hu Yingguo, Lu Wenyuan, Jin Xuhao, et al. Numerical simulation for excavation blasting dynamic damage of rock high slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2012，31(11)：2204-2213.

[12] 单仁亮，宋立伟，白瑶，等.爆破作用下冻结岩壁损伤评价的模型试验研究[J].岩石力学与工程学报，2014，33(10)：1945-1952. Shan Renliang, Song Liwei, Bai Yao, et al. Model test studies of damage evaluation of frozen rock wall under blasting loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2014，33(10)：1945-1952.

[13] Xiao J Q, Ding D X, Jiang F L, et al. Fatigue damage variable and evolution of rock subjected to cyclic loading[J]. International Journal of Rock Mechanics and Mining Sciences, 2010，47(3)：461-468.

[14] Casas-Rodriguez J P, Ashcroft I A, Silberschmidt V V. Damage evolution in adhesive joints subjected to impact fatigue[J]. Journal of Sound and Vibration, 2007，308(3)：467-478.

[15] Martino J B, Chandler N A. Excavation-induced damage studies at the underground research laboratory[J]. International Journal of Rock Mechanics and Mining Sciences, 2004，41(8)：1413-1426.

[16] 崔广心.相似理论与模型试验[M].徐州：中国矿业大学出版社，1990.

[17] Zhong Guosheng, Ao Liping, Zhao Kui. Influence of explosion parameters on wavelet packet frequency band energy distribution of blast vibration[J]. Journal of Central South University, 2012，19(9)：2674-2680.

(责任编辑 丁 峰)

Model experimental studies of vibration effect and damage evolution of tunnel’s surrounding rock under cyclic blasting excavation

Zhong Guosheng1, Ao Liping1, Fu Yuhua2

(1.SchoolofArchitectureandCivilEngineering,HuizhouUniversity,Huizhou516007,Guangdong,China;2.CollegeofAppliedScience,JiangxiUniversityofScienceandTechnology,Ganzhou341000,Jiangxi,China)

In this work, based on the similarity theory, we conducted a model experiment to study the vibration effect and damage evolution of rocks surrounding a tunnel in push-type cyclic blasting excavation. The model was constructed with a ratio of 1∶15. By simulating the tunnel excavation of push-type cyclic blasting, we explored the influence of the change of blasting parameters on the vibration effect. The degree of the damage of the surrounding rock was evaluated by the change of the acoustic velocity at the same measuring point after blasting. The relationship between the damage evolution of the surrounding rock and the times of blasting was established. We arrived at the following results: (1) When the maximum section dose was about the same, the influence of the initiation section number on the dielectric coefficient (K) of Sodev formula was very small, but it was great on the attenuation coefficient of Sodev formula; (2) In push-type cyclic blasting excavation, there was a great difference in the decrease rates of the acoustic velocity among the measuring points with the same distance to the blasting region at the same depth, and the blasting damage ranges of the surrounding rock were typically an isotropic in terms of both depth and width; (3) When the blasting parameters were basically the same, the growth trend of the cumulative acoustic velocity’s decrease rate at the measuring point was nonlinear in different cyclic blasting excavation; (4) There were nonlinear evolution characteristics between the blasting cumulative damage (D) of the surrounding rock and the times of blasting (n) under push-type cyclic blasting loading, and different measuring points had different blasting cumulative damage propagation models. The closer the measuring point was to the explosion source, the faster the cumulative damage extension. Blasting cumulative damage effect of the surrounding rock had typically nonlinear evolution properties and anisotropic characteristics.

mechanics of explosion; vibration effect; model experiment; tunnel excavation; cyclic blasting load; surrounding rock damage

10.11883/1001-1455(2016)06-0853-08

2015-03-25； < class="emphasis_bold">修回日期：2015-06-26

2015-06-26

国家自然科学基金项目(51064009，51464015)；广东省高等学校人才引进专项项目(A413.0210)； 广东省自然科学基金项目(2016A030313121)；惠州市科技项目(2014B020004018)

中国生(1974— )，男，博士,zgs1001@163.com。

O383.1;TV554 <国标学科代码：1303520 class="emphasis_bold"> 国标学科代码：1303520 文献标志码：A国标学科代码：1303520

A